Impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease using a mathematical model

Chacha M. Issarow; Nicola Mulder; Robin Wood

doi:10.12688/f1000research.12757.1

Home Browse Impact of effective contact rate and post treatment immune status...

ALL Metrics

-

Views

-

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease using a mathematical model

[version 1; peer review: 1 approved with reservations, 1 not approved]

Chacha M. Issarow¹, Nicola Mulder¹, Robin Wood²

PUBLISHED 09 Oct 2017

Author details Author details

¹ Computational Biology Division, Department of Integrative Biomedical Sciences, Institute of Infectious Disease and Molecular Medicine, Faculty of Health Sciences, University of Cape Town, Cape Town, 7925, South Africa
² The Desmond Tutu HIV Centre, Institute of Infectious Disease and Molecular Medicine, Faculty of Health Sciences, University of Cape Town, Cape Town, 7925, South Africa

Chacha M. Issarow
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Project Administration, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Nicola Mulder
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Robin Wood
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Resources, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Bioinformatics gateway.

This article is included in the World TB Day collection.

Abstract

Background: Tuberculosis (TB) disease burden is determined by both infection and progression rate to disease. Progression rate varies by immune status, with prior infection in high burdened settings significantly reducing the progression to disease from subsequent reinfections and completion of successful treatment associated with increased risk of subsequent TB disease. Novel studies of TB vaccines are now underway targeting high risk individuals who have completed successful combination TB chemotherapy for active TB.
Methods: In our study, we explored the impact of effective contact rate (β) and post-treatment immune status on population TB burden using a mathematical model incorporating five immunological states; susceptible, newly infected, reinfected, active TB and treated TB.
Results: We found that the number of newly infected individuals increased with increasing values of β< 10yr^-1, but declined when β> 10yr^-1. Corresponding numbers of reinfected individuals increased with increasing values of β irrespective of post-treatment immune status. Furthermore, we noted that the number of active TB cases decreased by 7 - 17% when treated individuals moved to either newly infected or reinfected immune states, respectively, rather than to the fully susceptible state at values of β< 10yr^-1. The corresponding declines in TB burden were only 2 - 7% at values of β> 10yr^-1. Results show that TB prevalence in high burden settings is primarily driven by effective contact rates, which are significantly modified by pre- and post-treatment immune factors.
Conclusions: The observation that impact of post-treatment immune status modification on population burden may be diminished in very high burdened settings will be important for vaccine design.

Keywords

Contact rate, Immunological memory, Mathematical model, Eigenvalue Stability point

Corresponding author: Chacha M. Issarow

Competing interests: The authors declare no competing interests.

Grant information: This work is funded by grants from the South African Medical Research Council with funds from National Treasury under the Economic Competitiveness and Support Package (MRC-RFA-UFSP-01-2013/CCAMP) and the Bill & Melinda Gates Foundation (OPP1116641).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2017 Issarow CM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Issarow CM, Mulder N and Wood R. Impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease using a mathematical model [version 1; peer review: 1 approved with reservations, 1 not approved]. F1000Research 2017, 6:1817 (https://doi.org/10.12688/f1000research.12757.1) First published: 09 Oct 2017, 6:1817 (https://doi.org/10.12688/f1000research.12757.1) Latest published: 09 Oct 2017, 6:1817 (https://doi.org/10.12688/f1000research.12757.1)

Introduction

Tuberculosis (TB) transmission results from air exchange between infective sources and susceptible individuals within enabling environments. Enabling environments are frequently poorly ventilated congregate settings, such as households, public transport, schools, and work places, resulting in high effective contact rate between infectious and susceptible individuals^1,2.

Effective contact number is determined by the effective contact rate and the mean period of infectiousness of source cases. Progression from TB infection to disease depends on the interaction between the immunological state of the host and the virulence of the pathogen strain³. TB disease may arise either early or late following a new infection and also from reinfection of previously infected cases. Substantial epidemiological evidence suggests that reinfection is among the factors hampering successful TB control^4,5 and is a major contributor to active disease in both high and low TB burden settings⁶.

Individuals treated with combination chemotherapy for active disease have high rates of re-treatment, due to both reactivation and reinfection, and contribute 30% of total TB notifications in high burdened settings⁷. Treated TB cases therefore constitute an attractive target for vaccine studies because of a high new TB event frequency and ease of identification. Two recent studies of TB vaccines are currently exploring a novel strategy of vaccination in individuals who have had successfully treated active TB^8,9. However, the biological mechanisms for high rates of re-treatment and the immune status following successful treatment remain unclear.

This paper describes a mathematical model that incorporates susceptible, newly infected, reinfected, active TB and treated individuals to study the population impact of effective contact rate and post-treatment immune status on TB epidemiology. An infectious individual with varying effective contact rate (ranging from 5 to 30 y r^–1) was introduced among 100, 000 fully susceptible individuals and we observed the number of individuals in all five states at stability point of a TB epidemic. This range of effective contact rate was selected because β = 5−10 y r^–1 is related to TB transmission in the United Kingdom in 1900 − 1950⁴, β = 15 y r^–1 is related to TB transmission in schools in South Africa², and β = 30 y r^–1 is related to TB transmission in prisons in South Africa¹⁰. Here, we explore the population impact of effective contact rate by comparing the number of newly infected and that of reinfected individuals at stability point of a TB epidemic, with increasing effective contact rate. The study was divided into three parts and simulated the model numerically when all treated individuals move to: (i) susceptible (ii) newly infected or (iii) reinfected state, and we observed the number of individuals in all five states. We explore the population impact of post-treatment immune status by comparing the number of active TB cases when all treated individuals move to either a susceptible, newly infected or reinfected state with increasing effective contact rate. This is an important study population as the incidence of TB can be higher in people recently cured of the disease. We compute the basic reproduction number and eigenvalues from the model when treated individuals move to all three states of susceptible, newly infected and reinfected to examine the stability of the disease free equilibrium.

Methods

Model design and development

The model consists of five states of susceptible individuals (S) who are not yet infected, but at a high risk of acquiring TB infection or disease if exposed to an infectious individual(s); newly infected individuals (L₁) who have been infected once in their lifetime with Mycobacterium tuberculosis (MTB) and if exposed, they move to either reinfected or active TB state through exogenous reinfection, depending on the host immune response and virulence of the pathogen strain; reinfected individuals (L₂) who have been infected multiple times with MTB of either the same or different strains and remain latently infected or move to active TB state through endogenous reactivation; active TB individuals (I) who are infectious and can transmit TB; treated or recovered individuals (T) who were previously infectious and were cured by chemotherapy, though some are still on treatment. Note that the difference between newly infected and reinfected individuals is that newly infected individuals are latently infected who have been infected once in lifetime with MTB and they can develop active disease through either exogenous reinfection or endogenous reactivation, while reinfected individuals are latently infected individuals who are multiply infected with MTB of either the same or different virulent strains and they can only develop active disease through endogenous reactivation or remain latently reinfected, depending on the virulence of the pathogen strain and immune response of the host.

The design and development of the model was based on an actual population in Cape Town, South Africa¹¹, where many already infected individuals are repeatedly exposed to different infectious sources and become reinfected, and start treatment after acquiring TB disease¹¹.

Furthermore, since natural MTB infection and chemotherapy induce an immune response that reduces TB susceptibility¹², we take into consideration the fact that treated individuals move to either a newly infected or reinfected state if they maintain immunological memory after successful treatment, and if they become susceptible due to waning of the immune response, they move to a susceptible state. This is because the average duration for the waning of induced immune response by MTB and chemotherapy is not well understood. However, if treatment fails or is not completed, they can move back to active disease and become infectious. As it has been reported that TB disease incidence in TB treated individuals is several-fold higher than in latently infected¹³, we explored post-treatment cases returning to either the susceptible, newly infected or reinfected immunological state. This approach makes our model unique and different from the prior studies, which apply infection force for treated individuals moving to latent TB states without considering immunological memory of the host. In order to explore the population impact of effective contact rate and post treatment immune status on TB epidemiology in high TB burden settings, such as Cape Town, the model includes human immunodeficiency virus (HIV) infection, but it does not incorporate: (i) age stratification or (ii) multi-drug resistant TB (MDR-TB).

Model description and assumptions

In the development of the model, we assume that the population consists of fully susceptible individuals, hence, the number of births or recruitment individuals become susceptibles at a rate π y r^–1. When susceptible individuals become infected with MTB, a proportion p in this group develop active TB very fast and it’s complement proportion 1−p, which constitute the majority become latently infected and move to a newly infected state depending on the virulent strains of the pathogen and host immunological factors. Newly infected individuals are at a high risk of developing active disease through either endogenous reactivation or exogenous reinfection. Here, we take into consideration that one group of newly infected individuals develop active TB slowly through endogenous reactivation at a rate c y r^–1, and a fraction q of the second group of newly infected individuals develop active TB very fast after infection through exogenous reinfection, while a remaining fraction 1-q of this group move to a reinfected state. Reinfected individuals develop active TB through endogenous reactivation either fast or slowly at a rate y y r^–1, depending on the immunological state of the host and the virulent strains of the infecting pathogen. Individuals with active TB receive medical treatment and move to a treated state at a rate k, while some die of active TB at a rate µ_t y r^–1. Treated and successfully cured individuals may become susceptible and move to a susceptible state at a rate r or retain immunological memory and move to either a newly infected at a rate g or a reinfected state at a rate z y r^–1, without exposure to the force of infection¹⁴. This is because latently infected and treated individuals acquire an immune response that reduces TB susceptibility though it may wane and individuals become susceptible. As mentioned earlier, we only implement treatment for active TB cases because in the real world, many TB patients only start treatment after active disease development. However, if TB cases are not well treated, treatment fails or chemotherapy is incomplete, they incubate the infection and relapse back to active TB at a rate α y r^–1. As stated earlier. it has been noted that latently infected individuals acquire immunity that reduces TB susceptibility^5,15, though they can be (re)infected and develop active disease if they become frequently exposed to infectious individuals in confined spaces. Thus, ω(0 < ω < 1) is the preventive factor due to prior natural MTB infection, which partially prevents latently infected individuals from TB susceptibility⁵. In each of the five states, there is a natural mortality rate µ y r^–1 as demonstrated in Figure 1.

Figure 1. TB transmission model to study the impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease.

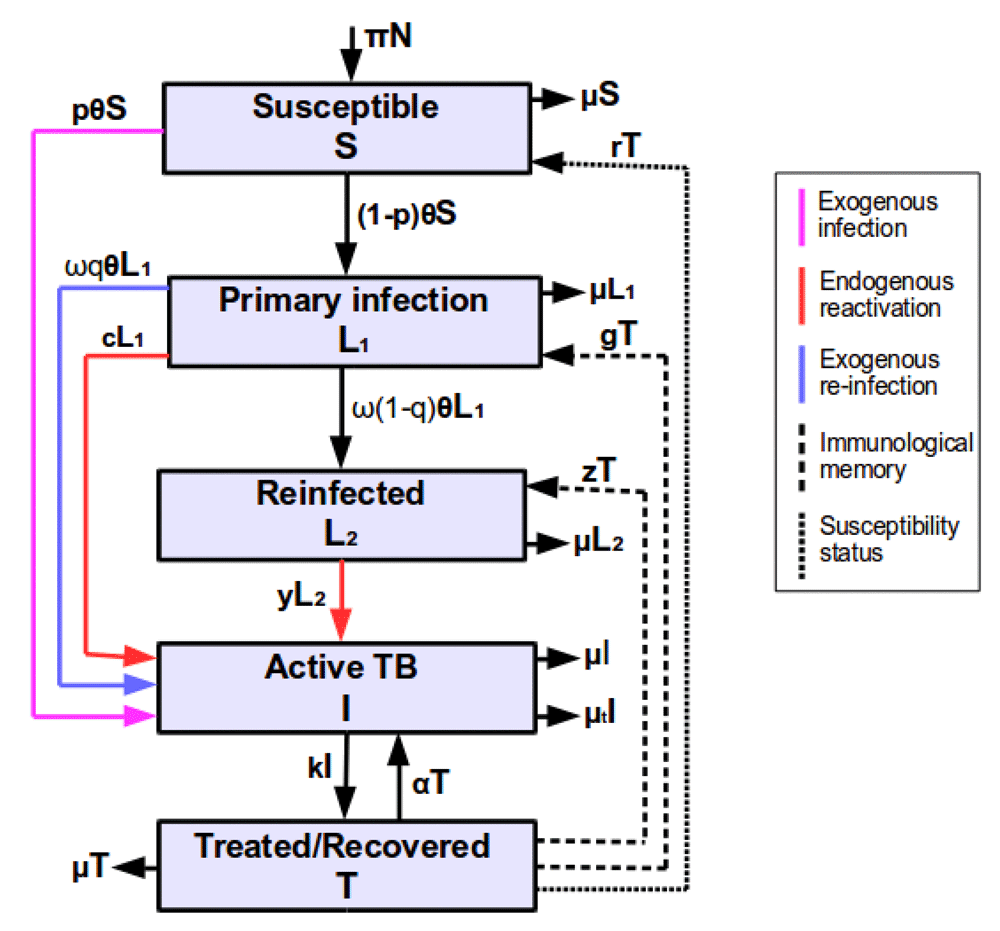
Parameters are described in Table 1.

From the model (Figure 1), we developed a mathematical model as follows:

\begin{array}{l} \dot{S} = π N - (θ + μ) S + r T \\ {\dot{L}}_{1} = (1 - p) θ S - (c + ω θ + μ) L_{1} + g T \\ {\dot{L}}_{2} = ω (1 - q) θ L_{1} - (y + μ) L_{2} + z T \\ \dot{I} = p θ S + (c + ω q θ) L_{1} + y L_{2} - (k + μ + μ_{t}) I + α T \\ \dot{Τ} = κ Ι - (r + z + g + α + μ) T \end{array}} (1)

where $θ = β \frac{I}{N},$ which is the force of infection, β is the effective contact rate, $\frac{I}{N}$ is the prevalence, I is the number of infectious individuals and N is the total number of individuals in the population. Other parameters are described in Table 1.

Disease free equilibrium is defined as the point at which there is no existence of the disease in the population. By computing S, L₁, L₂, I and T at disease free equilibrium (i.e., L₁ = L₂ = I = T = 0) and assuming that birth rate is equal to death rate, we obtain the disease free equilibrium point as $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ = (N, 0, 0, 0, 0). This implies that at disease free equilibrium, the total number of individuals in the population is equal to that of susceptible individuals, such that N = S. However, during an epidemic of active disease at any time, t, we have N_(t) = S_(t)+L_1(t)+L₂_(t)+I_(t)+T_(t), implying that the population is comprised of all five states and disease free equilibrium might be unstable. The model is epidemiologically balanced. From the mathematical model (Equation 1), we compute the basic reproduction number to determine the stability of the disease free equilibrium as discussed below.

Table 1. Description of parameters used in Figure 1.

The values of parameters used in this study were estimated from published literature. We also computed and estimated other values by matching infection and incidence data in South Africa.

Parameter	Description	Values	Reference
β	Effective contact rate	5 − 30 yr⁻¹	estimated
p	Probability of fast progression from susceptible to active TB after infection	0.05	16,17
c	Rate of progression from newly infected to active TB through endogenous reactivation	0.0026 yr⁻¹	16,17
q	Probability of moving from newly infected to active TB through exogenous reinfection	0.03	6
y	Rate of endogenous reactivation from reinfected to active TB	0.0053 yr⁻¹	16,17
r	Rate of moving from treated to susceptible state	Variable (0 or 0.99)	Depends on the immunological status
π	Birth or recruitment rate	0.02 yr⁻¹	18
g	Rate of moving from treated to a newly infected state	Variable (0 or 0.99)	Depends on the immunological status
ω	Preventive factor that reduces TB susceptibility due to prior natural MTB infection	0.21	8
z	Rate of moving from treated to a reinfected state	Variable (0 or 0.99)	Depends on the immunological status
k	Case detection rate from active TB to treated state	0.68 yr−¹	19
α	Rate of treatment failure and move to active TB	0.01 yr⁻¹	16
µ	Natural mortality rate	0.02 yr⁻¹	6
µ_t	Active TB mortality rate	0.075 yr⁻¹	19

Computed values: In the design of the model (Figure 1), we take into consideration that treated or recovered individuals may become either susceptible or immune, depending on the host immunological status. Thus, successful treatment to either g, r or z = 1 - treatment failure (α).

Basic reproduction number

Basic reproduction number (R_o) is the average number of secondary cases generated by a single case connected with the fully susceptible population^16,20,21. We use the next generation method to determine the basic reproduction number, which is an important figure in the epidemiology of infectious diseases. It is among the most frequently estimated quantities to predict the outbreak of infectious diseases, and its value provides information for designing control interventions for the infectious disease burden^16,21. R_o thus plays an important role in the analysis of infectious disease models, such as TB¹⁷. If R_o < 1, the disease free equilibrium is asymptotically stable, and it is unstable if R_o > 1^16,20,21.

The next generation method is used extensively to compute the basic reproduction number, though numerous other methods are discussed in the literature²¹. It generates a next generation matrix, and the basic reproduction number is the spectral radius of this matrix. The next generation matrix is defined as a matrix that relates the numbers of newly infected individuals in the various states in consecutive generations²¹. The dominant eigenvalue in a next generation matrix is referred to as the basic reproduction number. The next generation matrix (M) is defined mathematically as

M = F (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) V^{- 1} (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}),

and the basic reproduction number is the dominant eigenvalue of M. Where F $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ and V $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ are the transmission and transition matrices (n × n matrix) at disease free equilibrium, respectively. These are defined mathematically as

F (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) = [\frac{\partial f_{i} (x_{0})}{x_{j}}] and V (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) = [\frac{\partial v_{i} (x_{0})}{x_{j}}] for i, j = 1, \dots, n

where x_o is the disease free equilibrium, f_i is the rate of appearance of the new infection in classes, v_i is the transfer of the infection from one class to another and n is the number of infective classes.

However, prior to the formation of the next generation matrix, we generate the transmission (f) and transition (v) subsystems from Equation (1). We then linearise subsystems f and v by applying the Jacobian (J_c) and obtain matrices F(S, L₁, L₂, I, T) and V(S, L₁, L₂, I, T), which are n × n transmission and transition matrices, respectively. The transmission subsystem is an infected subsystem that describes the production of newly infected individuals and changes in the states of existing infected individuals. The transition subsystem is the transfer of the infection from one class to another. On the other hand, the transmission matrix describes the production of new infections, and the transition matrix describes changes of infected states, such as the immunity acquisition or removal by death²¹. Considering Equation (1), the Jacobian method that is used to linearise subsystems f and v is described mathematically as

J_{c} = (\begin{matrix} \frac{\partial \dot{S}}{\partial S} & \frac{\partial \dot{S}}{\partial L_{1}} & \frac{\partial \dot{S}}{\partial L_{2}} & \frac{\partial \dot{S}}{\partial I} & \frac{\partial \dot{S}}{\partial T} \\ \frac{\partial {\dot{L}}_{1}}{\partial S} & \frac{\partial {\dot{L}}_{1}}{\partial {\dot{L}}_{1}} & \frac{\partial {\dot{L}}_{1}}{\partial {\dot{L}}_{2}} & \frac{\partial {\dot{L}}_{1}}{\partial I} & \frac{\partial {\dot{L}}_{1}}{\partial T} \\ \frac{\partial {\dot{L}}_{2}}{\partial S} & \frac{\partial {\dot{L}}_{2}}{\partial {\dot{L}}_{1}} & \frac{\partial {\dot{L}}_{2}}{\partial {\dot{L}}_{2}} & \frac{\partial {\dot{L}}_{2}}{\partial I} & \frac{\partial {\dot{L}}_{2}}{\partial T} \\ \frac{\partial \dot{I}}{\partial S} & \frac{\partial \dot{I}}{\partial L_{1}} & \frac{\partial \dot{I}}{\partial L_{2}} & \frac{\partial \dot{I}}{\partial I} & \frac{\partial \dot{I}}{\partial T} \\ \frac{\partial \dot{T}}{\partial S} & \frac{\partial \dot{T}}{\partial L_{1}} & \frac{\partial \dot{T}}{\partial L_{2}} & \frac{\partial \dot{T}}{\partial I} & \frac{\partial \dot{T}}{\partial T} \end{matrix}) (2)

Hence, from Equation (1), we form the transmission, f and transition, v subsystems as

f = (\begin{matrix} \begin{matrix} 0 \\ (1 - p) β \frac{I}{N} S \end{matrix} \\ ω (1 - q) β \frac{I}{N} L_{1} \\ p β \frac{I}{N} S + ω q β \frac{I}{N} L_{1} \\ 0 \end{matrix}) and v = (\begin{matrix} \begin{matrix} - π N + (β \frac{I}{N} + μ) S - r T \\ (c + ω β \frac{I}{N} + μ) L_{1} - g T \end{matrix} \\ (y + μ) L_{2} - z T \\ c L_{1} - y L_{2} + (k + μ + μ_{t}) I - α T \\ - k I + (r + z + g + α + μ) T \end{matrix})

In Figure 1, there are three infected states, which are L₁, L₂ and I, giving a 3×3 matrix. Hence, we form the transmission matrix, F(S, L₁, L₂, I, T) by using Jacobian (see Equation (2)) in f for L₁, L₂ and I as

F (S, L_{1}, L_{2}, I, T) = (\begin{matrix} 0 & 0 & (1 - p) β \frac{S}{N} \\ ω (1 - q) β \frac{I}{N} & 0 & ω (1 - q) β \frac{L_{1}}{N} \\ ω q β \frac{I}{N} & 0 & p β \frac{S}{N} + ω q β \frac{L_{1}}{N} \end{matrix}) (3)

Substituting S, L₁, L₂, I and T at disease free equilibrium point $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ = (N, 0, 0, 0, 0) into Equation (3), we obtain the transmission matrix at disease free equilibrium, F $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ , as

F (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) = (\begin{matrix} 0 & 0 & (1 - p) β \\ 0 & 0 & 0 \\ 0 & 0 & p β \end{matrix}) (4)

By applying the Jacobian with respect to L₁, L₂ and I in v above, we obtain the transition matrix, V(S, L₁, L₂, I, T), as

V (S, L_{1}, L_{2}, I, T) = (\begin{matrix} c + ω β \frac{I}{N} + μ & 0 & ω β \frac{L_{1}}{N} \\ 0 & y + μ & 0 \\ - c & - y & k + μ + μ_{t} \end{matrix}) (5)

Substituting disease free equilibrium point into Equation (5), we obtain the transition matrix at disease free equilibrium, V $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ , as

V (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) = (\begin{matrix} c + μ & 0 & 0 \\ 0 & y + μ & 0 \\ - c & - y & k + μ + μ_{t} \end{matrix}) (6)

Since the transition matrix consists of many variables, to be consistent we used a computational tool (Sage version 8.0; http://www.sagemath.org/) to compute the inverse. Hence the inverse of Equation (6), V⁻¹ $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ , is demonstrated as

V^{- 1} (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) = (\begin{matrix} \frac{1}{c + μ} & 0 & 0 \\ 0 & \frac{1}{y + μ} & 0 \\ \frac{c}{(c + μ) (k + μ + μ_{t})} & \frac{y}{(y + μ) (k + μ + μ_{t})} & \frac{1}{k + μ + μ_{t}} \end{matrix}) (7)

We obtain the next generation matrix, which is the product of F $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ and V⁻¹ $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ as

F (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) V^{- 1} (S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o}) = (\begin{matrix} \frac{(1 - p) β c}{(c + μ) (k + μ + μ_{t})} & \frac{(1 - p) β y}{(y + μ) (k + μ + μ_{t})} & \frac{(1 - p) β}{k + μ + μ_{t}} \\ 0 & 0 & 0 \\ \frac{p β c}{(c + μ) (k + μ + μ_{t})} & \frac{p β y}{(y + μ) (k + μ + μ_{t})} & \frac{p β}{k + μ + μ_{t}} \end{matrix}) (8)

Thus, the basic reproduction number, which is defined as the dominant eigenvalue in the next generation matrix, was obtained from Equation (8) as

R_{o} = \frac{β (μ p + c)}{(k + μ + μ_{t}) (μ + c)}

The computed basic reproduction number has a positive real part, implying that it might be greater than 1. We further examined the stability of the disease free equilibrium by computing eigenvalues as discussed below.

Stability analysis of the disease free equilibrium

Since the basic reproduction number computed in this study has a positive real part, it is likely to be greater than 1, implying that TB transmission is increasing, regardless of the implementation of medical treatment^16,20,21. Here, we explore the stability of the disease free equilibrium by computing eigenvalues in Equation (1). Disease free equilibrium is stable if all eigenvalues have negative real parts, and unstable if any of the eigenvalues is positive²⁰. Hence, applying the Jacobian in Equation (1), gives

J = (\begin{matrix} - (β \frac{I}{N} + μ) & 0 & 0 & - β \frac{S}{N} & r \\ (1 - p) β \frac{I}{N} & - (c + ω β \frac{I}{N} + μ) & 0 & (1 - p) β \frac{S}{N} - ω β \frac{L_{1}}{N} & g \\ 0 & ω (1 - q) β \frac{I}{N} & - (y + μ) & ω (1 - q) β \frac{L_{1}}{N} & z \\ p β \frac{I}{N} & c + ω β \frac{I}{N} & y & H & α \\ 0 & 0 & 0 & k & - (r + α + z + g + μ) \end{matrix}) (9)

where $H = p β \frac{S}{N} + ω β \frac{L_{1}}{N} - (k + μ + μ_{t})$

The characteristic equation of the model at disease free equilibrium is expressed as

[J_{_0–λI}] = 0

where J₀ is the Jacobian matrix (from the model) at disease free equilibrium, λ is the eigenvalue and I is the identity matrix.

Substituting disease free equilibrium point $(S^{o}, L_{1}^{o}, L_{2}^{o}, I^{o}, T^{o})$ = (N, 0, 0, 0, 0) into Equation (9), minus the product of eigenvalue and identity matrix diagonally, we obtain the model matrix at disease free equilibrium as follows:

(J_{0} - λ I) = (\begin{matrix} - μ - λ & 0 & 0 & - β & r \\ 0 & - c - μ - λ & 0 & (1 - p) β & g \\ 0 & 0 & - y - μ - λ & 0 & z \\ 0 & c & y & p β - (k + μ + μ_{t}) - λ & α \\ 0 & 0 & 0 & k & - r - α - z - g - μ - λ \end{matrix}) (10)

From Equation (10), we form the characteristic equation, [J_0−λI] = 0, as

(–μ – λ)[(–c – μ – λ)(–y – μ – λ)(pβ – k – μ – μ_t – λ)(–r – α – z – g – μ – λ)]

–c[(–y – μ – λ)(pβ – k – μ – μ_t – λ)(–r – α – z – g – μ – λ)] = 0

Simplifying the characteristic equation further, gives

(–y – μ – λ)(pβ – k – μ – μ_t – λ)(–r – α – z – g – μ – λ)[μ(c + μ) + λ(2μ + c + λ) – c] = 0

From the simplified characteristic equation, we form the following four equations:

–(y + μ) – λ = 0 (11)

pβ – (k + μ + μ_t) – λ = 0 (12)

–(r + α + z + g + μ) – λ = 0 (13)

λ² + (2μ + c)λ + μ² + cμ – c = 0 (14)

Using Equation (11) to Equation (14), we can determine the eigenvalues that predict the stability of the disease free equilibrium. As mentioned earlier, disease free equilibrium is stable if all eigenvalues have negative real parts, and unstable if any of the eigenvalues is positive. Additionally, if one of the eigenvalues is zero then we cannot tell from stability analysis whether the disease free equilibrium is stable or unstable. Thus, considering Equation (11) to Equation (14), the eigenvalues are:

λ₁ = –(y + μ) < 0

λ₂ = pβ – (k + μ + μ_t)

λ₃ = –(r + α + z + g + μ) < 0

λ_{4, 5} = \frac{- (2 μ + c) \pm \sqrt{{(2 μ + c)}^{2} - 4 (μ^{2} + c μ - c)}}{2}

Here, we noted that λ₁ and λ₃ have negative real parts, and λ₂ has a positive real part if pβ > (k + µ + µ_t). For stability of the disease free equilibrium, we assume that λ_4,5 have negative real parts (i.e., λ₄ < 0 and λ₅ < 0). Disease free equilibrium is stable if pβ < (k + µ + µ_t) and unstable if pβ > (k + µ + µ_t), where pβ is the effective contact rate for susceptible individuals moving directly to active disease. On the other hand, disease free equilibrium is stable if the effective contact rate for susceptible individuals moving directly to active disease is less than the summation of case detection, natural death and disease death rates. Otherwise disease free equilibrium is unstable.

Results from numerical analysis

Using data estimated from published literature, varying effective contact rate (ranging from β = 5 to β = 30 y r^–1) and computed or estimated values by matching infection and incidence data in South Africa (Table 1), we simulated Equation (1) numerically to explore the population impact of effective contact rate and post treatment immune status on TB epidemiology. As mentioned earlier, the study was divided into three parts where we simulated the model when all treated individuals move to: (i) susceptible (i.e., z = g = 0, r = 0.99 y r^–1) (ii) reinfected (i.e., r = g = 0, z = 0.99 y r^–1) or (iii) newly infected state (i.e., r = z = 0, g = 0.99 y r^–1). In the model simulation, we used the initial assumption that S = 100, 000, L₁ = L₂ = T = 0 and I = 1, implying that an infectious individual was introduced among 100, 000 fully susceptible individuals. The epidemic was observed for 700 years when β = 5 y r^–1 and 200 years when β ≥ 10 y r^–1 so that the TB epidemic stability point could be attained.

Here, we observed the number of individuals in all five states at stability point of a TB epidemic with increasing effective contact rate, and compared the number of newly infected and that of reinfected individuals. We also compared the number of active TB cases schematically when all treated individuals move to a susceptible, newly infected or reinfected state at stability point of a TB epidemic. We found that the number of newly infected cases increases when β = 5 to β = 10 y r^–1, then decreases with increasing effective contact rate, while that of reinfected individuals increases in all values of effective contact rate (Figure 2, Figure 4 and Figure 5), implying that a large number of active TB cases might be contributed by repeatedly exposed individuals. The number of active TB individuals was increasing with increasing effective contact rate, but lower than that of newly infected and reinfected individuals. Of all five states, the number of treated individuals was noted to be the lowest, probably because treated individuals become either susceptible and move to a susceptible state or retain immunological memory and move to either a newly infected or reinfected state. We noted that as the effective contact rate increases, the number of susceptible individuals decreases dramatically with a steep slope until a stability point is attained, implying that effective contact rate is an important factor, which determines the likelihood of TB infection and disease in the community. Table 2, Table 3 and Table 4 summarise simulation results in Figure 2, Figure 4 and Figure 5, which are magnified and visualised in Figure 7, Figure 8 and Figure 9 with increasing effective contact rate, while Figure 6 compares active TB cases.

Figure 2. Numerical simulation of Equation (1) when all treated individuals move to a newly infected state from β = 5 to β = 30 y r^–1.

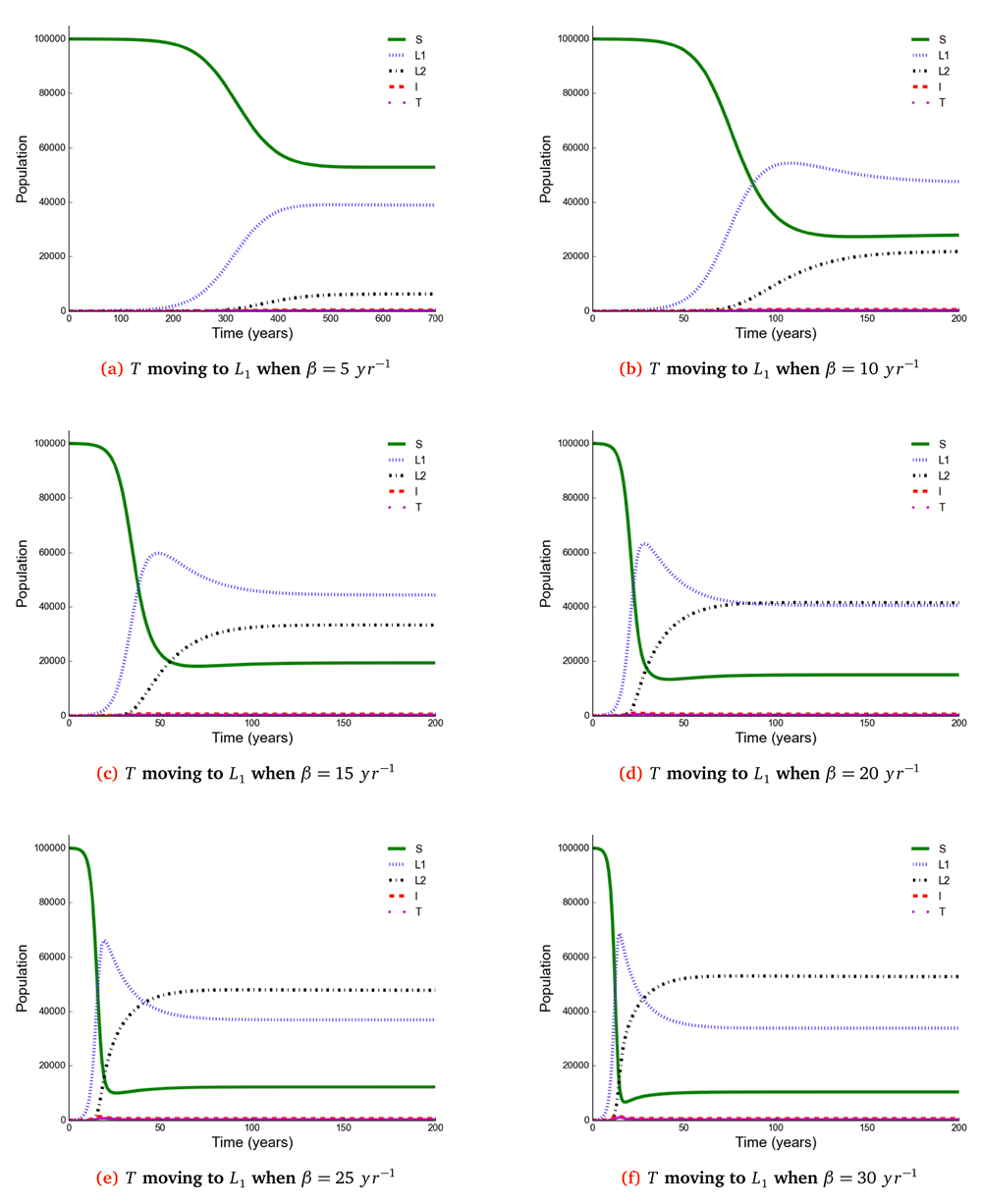
The number of individuals in all five states from β = 5 to β = 30 y r^–1 at stability point of a TB epidemic are shown in Table 2. Note: S = susceptible, L₁ = newly infected, L₂ = reinfected, I = active TB, T = treated.

Table 2. Comparison of the number of individuals in all five states at stability point of a TB epidemic, when all treated individuals move to a newly infected state with increasing effective contact rate (Figure 2).

Effective contact rate	Susceptible	Newly infected	Reinfected	Treated	Active TB
5	52232	37767	5089	197	289
10	27053	46607	20625	319	469
15	18482	43392	32142	351	515
20	14196	39375	40714	364	535
25	11250	35625	46607	371	545
30	9642	32946	51428	375	550

Table 3. Comparison of the number of individuals in all five states at stability point of a TB epidemic, when all treated individuals move to a reinfected state with increasing effective contact rate (Figure 4).

Effective contact rate	Susceptible	Newly infected	Reinfected	Treated	Active TB
5	56517	27589	11517	177	260
10	28928	37232	28392	298	438
15	19821	35089	39107	330	484
20	15000	32678	46607	344	505
25	12053	30000	52500	351	515
30	9910	27053	56785	354	520

Table 4. Comparison of the number of individuals in all five states at stability point of a TB epidemic, when all treated individuals move to a susceptible state (Figure 5).

Effective contact rate	Susceptible	Newly infected	Reinfected	Treated	Active TB
5	62678	29732	2646	212	311
10	32142	43660	19017	330	484
15	21964	41517	30800	357	525
20	16607	37767	39375	371	545
25	13392	34821	45803	379	556
30	11250	31607	50892	382	561

Observing the number of active TB cases when treated individuals move to a susceptible, newly infected or reinfected state, we noted the highest number of active TB cases when all treated individuals move to a susceptible state (Table 2, Table 3 and Table 4). We went on to compare the number of active TB cases schematically when treated individuals move to a susceptible, newly infected or reinfected state and found that when all treated individuals become susceptible, the number of active TB cases becomes higher than moving to either a newly infected or reinfected state (Figure 6), perhaps because individuals moving to a newly infected or reinfected state have more protection due to immunological memory retention than susceptible individuals.

We separated and compared the number of active TB cases due to new infection (new active cases) and reactivation (reactivation cases) when treated individuals move to a susceptible, newly infected and reinfected state with increasing effective contact rate. We noted that new active cases are very dependent on the effective contact rate and highest when treated individuals move to a susceptible state, while reactivation cases plateau when β > 10 y r^–1 (Figure 3).

Figure 3. Separation and comparison of new infection and reactivation active TB cases when all treated individuals (T) move to a susceptible (S), newly infected (L₁) or reinfected state (L₂).

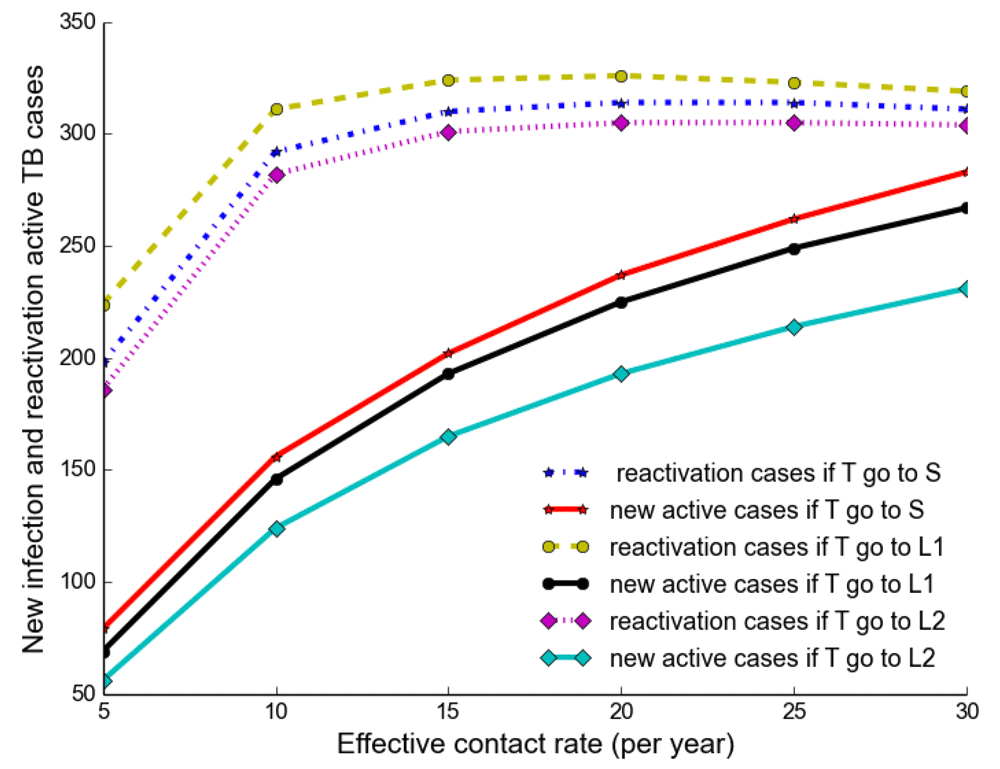
It shows that new active cases are very dependent on effective contact rate and highest when treated individuals move to a susceptible state, but reactivation cases plateau at the effective contact rate greater than 10 y r^–1.

Figure 4. Numerical simulation of Equation (1) when all treated individuals move to a reinfected state from β = 5 to β = 30 y r⁻¹.

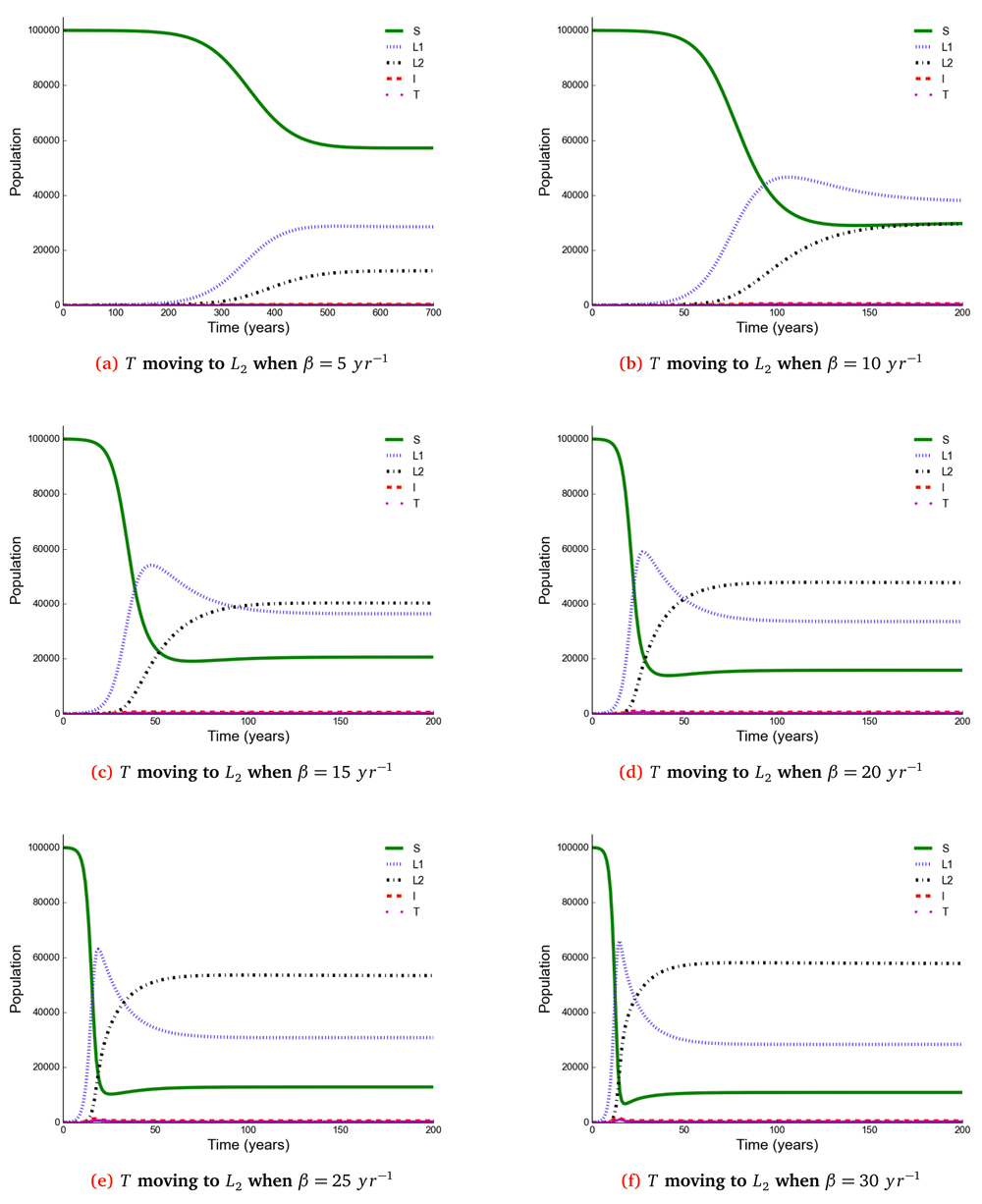
The number of individuals in all five states from β = 5 to β = 30 y r⁻¹ at stability point of a TB epidemic are shown in Table 3. Note: S = susceptible, L₁ = newly infected, L₂ = reinfected, I = active TB, T = treated.

Figure 5. Numerical simulation of a mathematical model (Equation (1)) to explore the impact of effective contact rate (β) varying from 5 to 30 yr⁻¹ among 100, 000 completely susceptible individuals, when all treated move to a susceptible state.

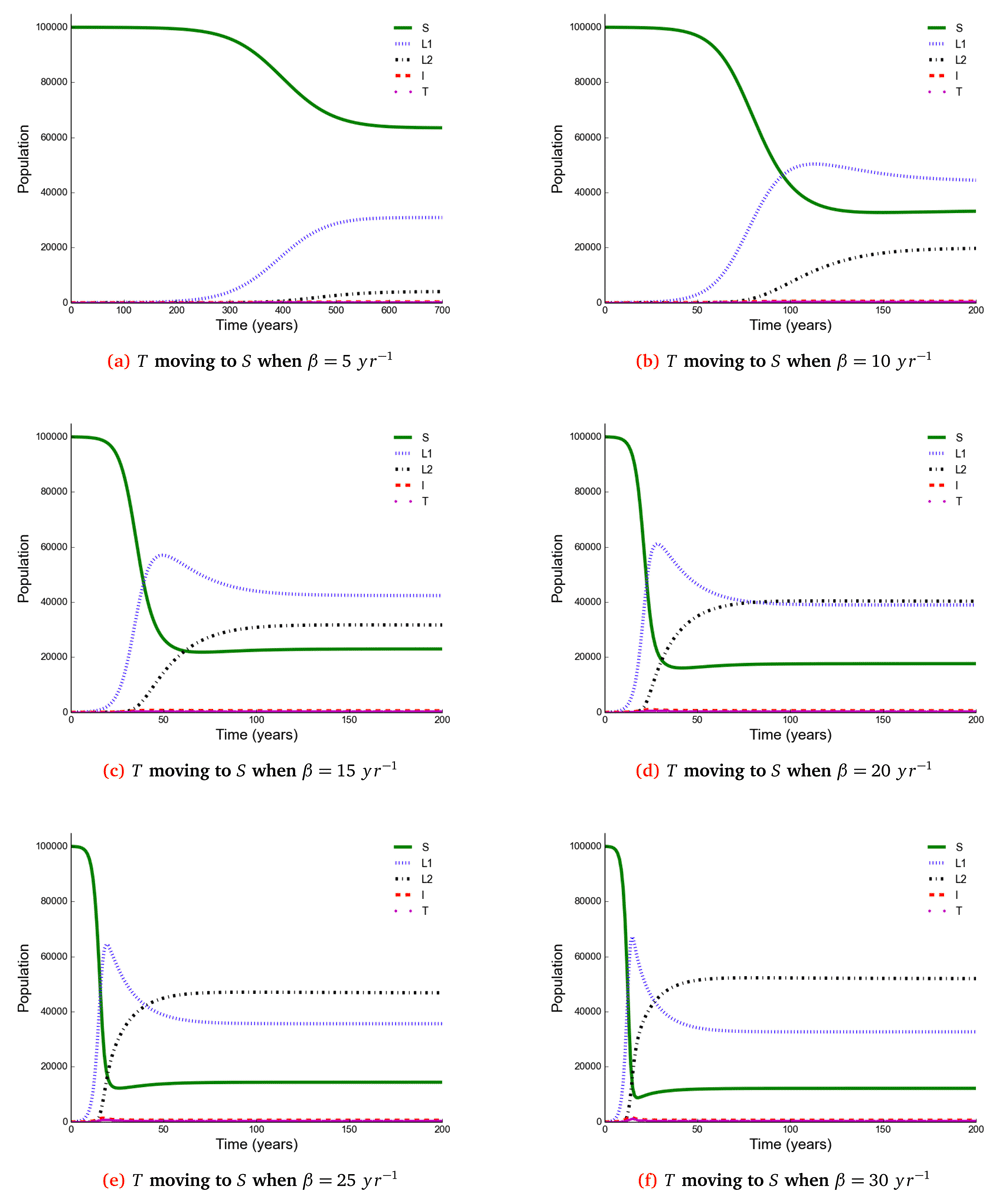
The number of individuals in all five states from β = 5 to β = 30 y r^–1 at stability point of a TB epidemic are shown in Table 4. Note: S = susceptible, L₁ = newly infected, L₂ = reinfected, I = active TB, T = treated individuals.

Figure 6. Comparison of active TB cases when all treated individuals (T) move to either a susceptible (S), newly infected (L₁) or reinfected state (L₂) at stability point of a TB epidemic (Table 2–Table 4).

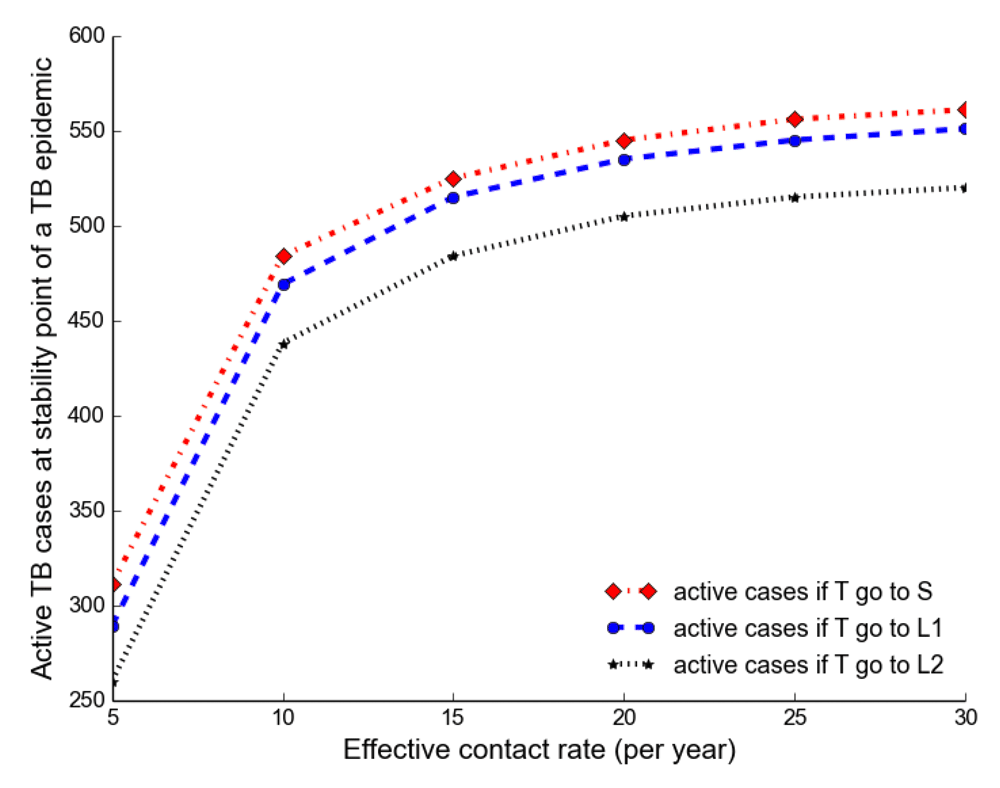
The number of active TB becomes higher when all treated individuals become susceptible than moving to either a newly infected or reinfected state.

Figure 7. Number of individuals per 100, 000 when all treated individuals move to a newly infected state with increasing effective contact rate from 5 to 30 y r^–1 (Table 2).

Susceptible (S), newly infected (L₁) and reinfected (L₂) are located on the left side of y-axis, while active TB (I ) and treated (T) are located on the right side of y-axis.

Figure 8. Number of individuals per 100, 000 when all treated individuals move to a reinfected state with increasing effective contact rate from 5 to 30 y r^–1 (Table 3).

Susceptible (S), newly infected (L₁) and reinfected (L₂) are located on the left side of y-axis, while active TB (I) and treated (T) are located on the right side of y-axis.

Figure 9. Number of individuals per 100, 000 when all treated individuals move to a susceptible state with increasing effective contact rate from 5 to 30 y r^–1 (Table 4).

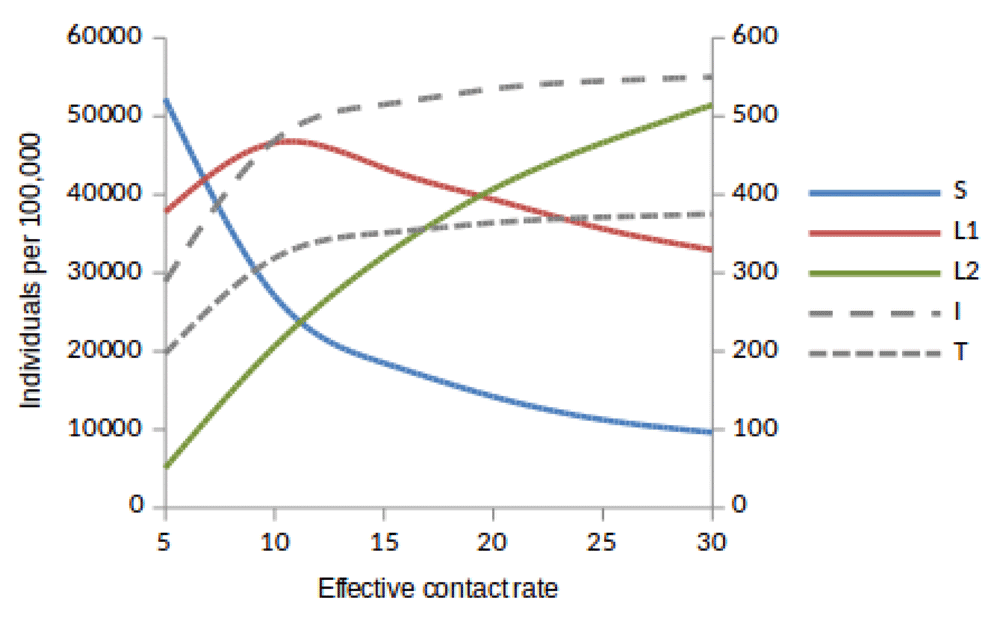
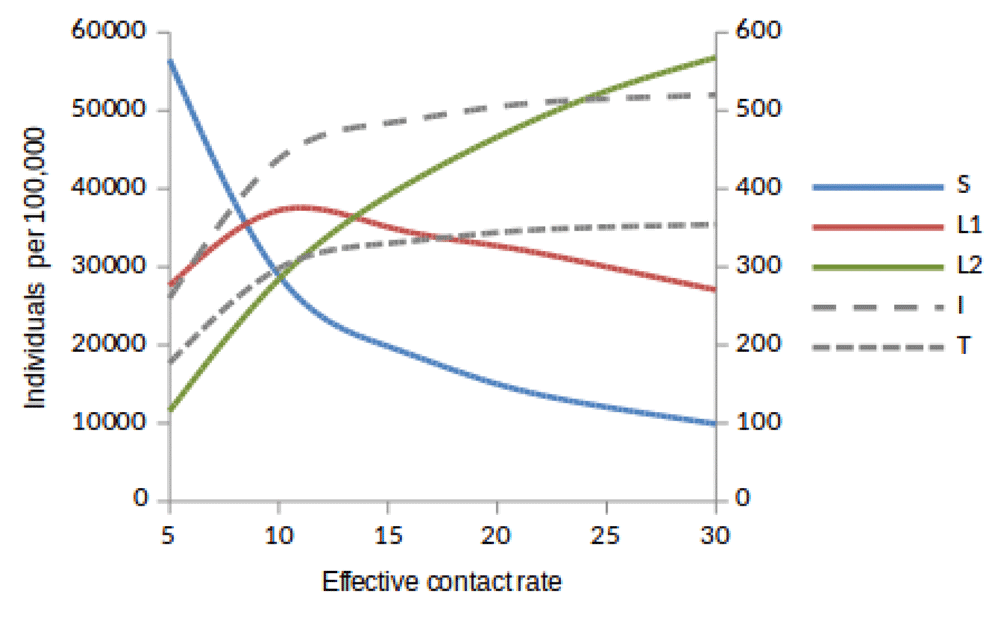
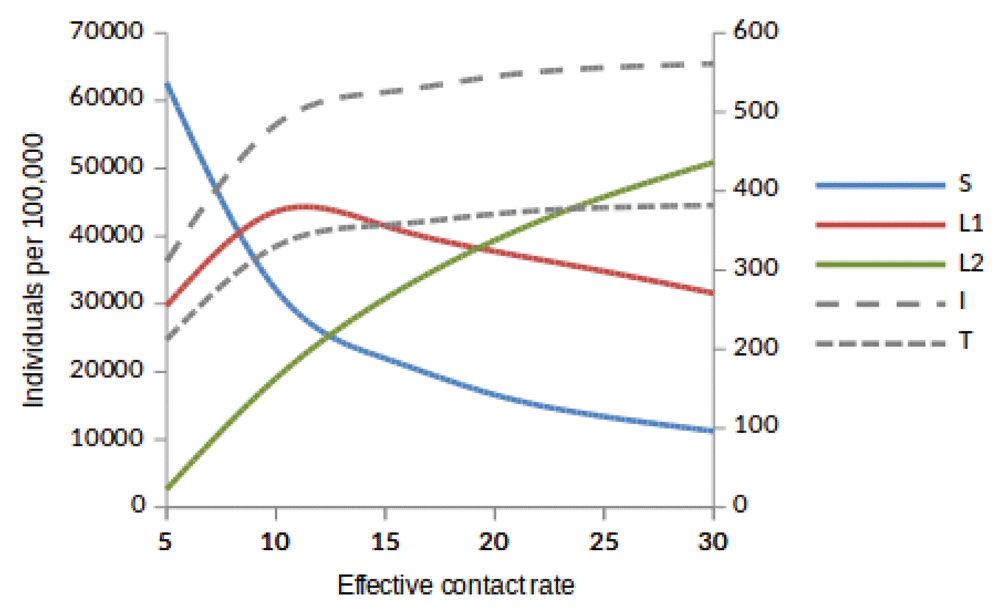
Susceptible (S), newly infected (L₁) and reinfected (L₂) are located on the left side of y-axis, while active TB (I) and treated (T) are located on the right side of y-axis.

The time taken for a TB epidemic to reach the peak and stability points was noted to decrease with increasing effective contact rate in all cases, implying that effective contact rate is directly correlated with the force of infection. Here, we show that the number of active TB cases in the community is contributed by both newly infected and reinfected individuals after developing active disease. However, since the number of reinfected individuals becomes higher than that of newly infected individuals at stability point of a TB epidemic (if β ≥ 20 y r^–1), TB prevalence might be driven by reinfection force.

Discussion

Using a mathematical model developed in this study, we investigated the impact of effective contact rate and post-treatment immune status on TB epidemiology. A caveat is that this is a simple model assuming a homogeneous population without age stratification and HIV. However, the model has important findings: Susceptible (S), newly infected (L₁), reinfected (L₂), active TB (I), and treated (T) individuals are all affected in a non-linear relationship with effective contact rate. While it is intuitive that the number of susceptible individuals declines with increasing effective contact rate, the other states are more complex. When β < 20 then L₁ > L₂ if T move to either S or L₁, and when β ≥ 20 then L₂ > L₁. Treatment and active TB rates are also non-linear, if effective contact rate decreases from 30 to 25 y r^–1 then the decline in TB cases is 5/100, 000, but a reduction of 10 to 5 y r^–1 produces a decline of 177(range, 173−180)/100, 000.

This saturation effect resulting from high effective contact rate may explain the difficulty in TB control in very high burdened settings, such as mines and prisons.

This may also explain the empiric finding that TB notification rates are relatively insensitive to moderate improvements in case finding in high burden settings. E.g. the Zamstar study and the World Health Organization observation of very little data on the impact of enhanced case finding in high burdened settings²². This is also compatible with the modelling of TB transmission in South African prisons¹⁰. At high effective contact rate (i.e., β ≥ 20), there is a high proportion of cases from L₂ rather than L₁. This is compatible with the observation that 20 − 25% of TB cases are re-treatment cases in high TB burden settings, such as Cape Town. Post-treatment immunological boosting from susceptible status (S) to latently infected status (L₂) could decrease population TB by 17% at lower effective contact rate but only 7% at high effective contact rate. Post-treatment vaccination impact would therefore be reduced in very high transmission settings. This finding is of considerable importance for post TB vaccine study design, requiring a balance between high event frequency and reduced vaccination effect.

The early peak values in TB rates demonstrate that there may be temporary peaks followed by apparent decline in notifications when TB disease is introduced into a new susceptible population, as seen in studies of the Alaskan Inuit population²³. The time course of TB epidemiology is long, and the status of the post-treatment state is something that prior models have ignored. Loss of protective immunity in newly infected individuals following treatment (or prophylaxis which is a form of treatment) could have major negative epidemiological consequences.

The findings in this study suggest that TB prevalence is driven by reinfection force, particularly in high TB burden settings, such as Cape Town. Although prior natural MTB infection induces a partial immune protection, which reduces TB susceptibility¹², the number of reinfected individuals continues to increase dramatically. The source of reinfection strains is not clearly understood, but the increasing number of reinfected individuals might be accelerated by the force of infection due to high effective contact rate and duration of exposure in congregate areas in particular. In conclusion, enhancing post-treatment immune status by vaccination may significantly augment medical treatment. However, an increased focus on diminishing the effective contact rate will require greater focus on environmental interventions.

Data availability

All the data sources used in the analysis are referenced in Table 1.

Competing interests

The authors declare no competing interests.

Grant information

This work is funded by grants from the South African Medical Research Council with funds from National Treasury under the Economic Competitiveness and Support Package (MRC-RFA-UFSP-01-2013/CCAMP) and the Bill & Melinda Gates Foundation (OPP1116641).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgements

This article is based on the PhD thesis of CI at the University of Cape Town, South Africa.

Faculty Opinions recommended

References

1. Andrews JR, Morrow C, Walensky RP, et al.: Integrating social contact and environmental data in evaluating tuberculosis transmission in a South African township. J Infect Dis. 2014; 210(4): 597–603. PubMed Abstract | Publisher Full Text | Free Full Text
2. Wood R, Morrow C, Ginsberg S, et al.: Quantification of Shared Air: A Social and Environmental Determinant of Airborne Disease Transmission. PLoS One. 2014; 9(9): e106622. PubMed Abstract | Publisher Full Text | Free Full Text
3. Nyabadza F, Winkler D: A simulation age-specific tuberculosis model for the Cape Town metropole. S Afr J Sci. 2013; 109(910): 1–7. Publisher Full Text
4. Vynnycky E, Fine PE: The natural history of tuberculosis: the implications of age-dependent risks of disease and the role of reinfection. Epidemiol Infect. 1997; 119(2): 183–201. PubMed Abstract | Publisher Full Text | Free Full Text
5. Gabriela M Gomes M, Rodrigues P, Hilker FM, et al.: Implications of partial immunity on the prospects for tuberculosis control by post-exposure interventions. J Theor Biol. 2007; 248(4): 608–617. PubMed Abstract | Publisher Full Text
6. Cohen T, Colijn C, Finklea B, et al.: Exogenous re-infection and the dynamics of tuberculosis epidemics: local effects in a network model of transmission. J R Soc Interface. 2007; 4(14): 523–531. PubMed Abstract | Publisher Full Text | Free Full Text
7. Middelkoop K, Bekker LG, Shashkina E, et al.: Retreatment tuberculosis in a South African community: the role of re-infection, HIV and antiretroviral treatment. Int J Tuberc Lung Dis. 2012; 16(11): 1510–1516. PubMed Abstract | Publisher Full Text | Free Full Text
8. Andrews JR, Noubary F, Walensky RP, et al.: Risk of progression to active tuberculosis following reinfection with Mycobacterium tuberculosis. Clin Infect Dis. 2012; 54(6): 784–791. PubMed Abstract | Publisher Full Text | Free Full Text
9. Fletcher HA, Schrager L: TB vaccine development and the End TB Strategy: importance and current status. Trans R Soc Trop Med Hyg. 2016; 110(4): 212–218. PubMed Abstract | Publisher Full Text | Free Full Text
10. Johnstone-Robertson S, Lawn SD, Welte A, et al.: Tuberculosis in a South African prison - a transmission modelling analysis. S Afr Med J. 2011; 101(11): 809–813. PubMed Abstract | Free Full Text
11. Hermans S, Horsburgh CR Jr, Wood R: A Century of Tuberculosis Epidemiology in the Northern and Southern Hemisphere: The Differential Impact of Control Interventions. PLoS One. 2015; 10(8): e0135179. PubMed Abstract | Publisher Full Text | Free Full Text
12. Gomes MG, Franco AO, Gomes MC, et al.: The reinfection threshold promotes variability in tuberculosis epidemiology and vaccine efficacy. Proc Biol Sci. 2004; 271(1539): 617–623. PubMed Abstract | Publisher Full Text | Free Full Text
13. Verver S, Warren RM, Beyers N, et al.: Rate of reinfection tuberculosis after successful treatment is higher than rate of new tuberculosis. Am J Respir Crit Care Med. 2005; 171(12): 1430–1435. PubMed Abstract | Publisher Full Text
14. Dye C, Gamett GP, Sleeman K, et al.: Prospects for global tuberculosis control under the WHO dots strategy. Distr: General WHO/TB 98.251. 1998. Reference Source
15. Fennelly KP, Jones-López EC: Quantity and quality of inhaled dose predicts immunopathology in tuberculosis. Front Immunol. 2015; 6: 313. PubMed Abstract | Publisher Full Text | Free Full Text
16. Blower SM, Mclean AR, Porco TC, et al.: The intrinsic transmission dynamics of tuberculosis epidemics. Nat Med. 1995; 1(8): 815–821. PubMed Abstract | Publisher Full Text
17. Sanchez MA, Blower SM: Uncertainty and sensitivity analysis of the basic reproductive rate. Tuberculosis as an example. Am J Epidemiol. 1997; 145(12): 1127–1137. PubMed Abstract | Publisher Full Text
18. South Africa Demographics Profile. 2014.
19. World Health Organization: Global tuberculosis report. 2015. Reference Source
20. van den Driessche P, Watmough J: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002; 180(1–2): 29–48. PubMed Abstract | Publisher Full Text
21. Diekmann O, Heesterbeek JA, Roberts MG: The construction of next-generation matrices for compartmental epidemic models. J R Soc Interface. 2010; 7(47): 873–885. PubMed Abstract | Publisher Full Text | Free Full Text
22. Kranzer K, Houben RM, Glynn JR, et al.: Yield of HIV-associated tuberculosis during intensified case finding in resource-limited settings: a systematic review and meta-analysis. Lancet Infect Dis. 2010; 10(2): 93–102. PubMed Abstract | Publisher Full Text | Free Full Text
23. Comstock GW, Baum C, Snider DE Jr: Isoniazid prophylaxis among Alaskan Eskimos: a final report of the bethel isoniazid studies. Am Rev Respir Dis. 1979; 119(5): 827–830. PubMed Abstract

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 09 Oct 2017

Author details Author details

¹ Computational Biology Division, Department of Integrative Biomedical Sciences, Institute of Infectious Disease and Molecular Medicine, Faculty of Health Sciences, University of Cape Town, Cape Town, 7925, South Africa
² The Desmond Tutu HIV Centre, Institute of Infectious Disease and Molecular Medicine, Faculty of Health Sciences, University of Cape Town, Cape Town, 7925, South Africa

Chacha M. Issarow
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Project Administration, Software, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Nicola Mulder
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Robin Wood
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Project Administration, Resources, Supervision, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

The authors declare no competing interests.

Grant information

This work is funded by grants from the South African Medical Research Council with funds from National Treasury under the Economic Competitiveness and Support Package (MRC-RFA-UFSP-01-2013/CCAMP) and the Bill & Melinda Gates Foundation (OPP1116641).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (1)

version 1

Published: 09 Oct 2017, 6:1817

https://doi.org/10.12688/f1000research.12757.1

Copyright

© 2017 Issarow CM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

0

SEE MORE DETAILS

CITE

how to cite this article

Issarow CM, Mulder N and Wood R. Impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease using a mathematical model [version 1; peer review: 1 approved with reservations, 1 not approved]. F1000Research 2017, 6:1817 (https://doi.org/10.12688/f1000research.12757.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 09 Oct 2017

Views

15

Reviewer Report 07 Feb 2018

James M. Trauer, School of Public Health and Preventive Medicine, Monash University, Melbourne, Australia

Not Approved

https://doi.org/10.5256/f1000research.13822.r30286

The strengths of the manuscript by Issarow et al. include that the article is clearly written, the large majority of the mathematical results appear to be correct to me and the work does build upon previous research. Unfortunately, the main ... Continue reading

The strengths of the manuscript by Issarow et al. include that the article is clearly written, the large majority of the mathematical results appear to be correct to me and the work does build upon previous research. Unfortunately, the main weakness is that the compartmental structure of the model fundamentally does not answer the question that has been posed.

The main reason for this is that transition from T to one of either S, L1 or L2 does not only capture a change to the relative immunity status of a person who has completed treatment, but also affects their infection status. That is, S, L1 and L2 also have different rates of endogenous reactivation to I (zero for S), as well as different rates of (re-)infection (zero for L2) and different proportions that progress to active disease immediately on infection. Therefore, the authors are really exploring the idea that treated individuals become fully susceptible and clear their infection (transition to S), behave as for once infected persons (transition to L1) or behave as for multiply infected persons (transition to L2 and remain immune from further infection) - in all respects. Perhaps it may be possible to argue that this is an exploration that is of interest and has a sound basis in epidemiology, but it is not the argument that the authors make and not the question they are seeking to answer. Also, it is unclear which of the multiple epidemiological differences differences between S, L1 and L2 is driving the observations.

Further, the reason for persons spending one year in the T compartment is unclear. If T is intended to represent persons under treatment (which is not what the authors argue) then this might be reasonable. However, in this case, the sojourn time in T should probably be six months, the alpha parameter should better represent relapse rates (and so be greater than 1% for Cape Town). Therefore, it is unclear what this state represents, other than that patients are fully immune from reinfection during their stay in T and are waiting to transition to a new susceptibility state.

The result for the basic reproductive number is doubtless correct and the method used to obtain it is well accepted. However, the formula can be calculated much more easily by simply taking the product of the number of infections per unit time in I (beta), the duration of time in I (1 / (k + mut + mu)) and the proportion of infections reaching I (which requires a small amount of algebra only). Similarly, stability analysis for the disease free equilibrium seems correct (although the calculations are a little beyond my mathematical ability), but there is no reason to doubt that the disease-free equilibrium would be stable. (Finding a second equilibrium at R0=1 and hence a backward bifurcation might perhaps be of more interest - however, as omega remains < 1 throughout the calculations, I do not believe such a phenomenon would be present.)

I have suggested reject as a decision for this manuscript, but am on the borderline between reject and major revision. I have also read the other reviewer's comments, which would also strengthen the paper and note her suggestion for a major revision. Therefore, I would be happy to review another version of the manuscript if the editors feel this is appropriate.

MINOR COMMENTS
Value of k for case detection is set at 0.68/year, but rationale is not described. Presumably this is the 2014 CDR estimate for South Africa. However, CDR is a proportion, so it cannot be simply incorporated into the model as a rate.
In the Methods it is stated that susceptible individuals have never been previously infected and L1 compartment individuals have only been infected once - however, this is only true if g=r=0, which is only the case in one configuration that is explored. Therefore these statements are misleading.
Prefer high-burden to high-burdened
Space between y and r-1 is unclear, should be just yr-1
Definitions of the transmission and transition matrices are unclear and seem incorrect.
Prefer lower limit of vertical axis of Figure 3 to be zero.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

No

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Tuberculosis, modelling, respiratory infections

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Respond or Comment

Views

14

Reviewer Report 05 Feb 2018

M. Gabriela M. Gomes, Liverpool School of Tropical Medicine, Liverpool, UK

Approved with Reservations

https://doi.org/10.5256/f1000research.13822.r28025

This paper presents a mathematical model for the transmission of tuberculosis in human populations, and describes how endemic equilibria change with effective contact rate and post treatment immune status.

The novelty of the model is the way ... Continue reading

This paper presents a mathematical model for the transmission of tuberculosis in human populations, and describes how endemic equilibria change with effective contact rate and post treatment immune status.

The novelty of the model is the way in which the latent infection compartment is slip into L1 and L2. The primary infection compartment (L1) consists of individuals who have been infected from a susceptible TB-free state (S) and were able to contain the infection in a latent state. These individuals are subject to reactivation and progression to active disease at a rate 0.0026 per year, and to reinfection at a rate 0.21 times the force of infection, where 0.21 accounts for reduced susceptibility due to prior infection. The reinfection compartment (L2) consists of those individuals who have been reinfected from L1 and were again able to contain the infection in a latent state. These individuals are now subject to reactivation and progression to active disease at an increased rate 0.0053 per year, but are no longer susceptible to subsequent reinfections. The model also provides the option for individuals who had active TB disease to return to S, L1 or L2 upon successful treatment. This seems sensible to me and so do the results, although I have not seen TB transmission models formulated in exactly this way before.

After defining the model, the authors proceed to calculating the basic reproduction number R0, the threshold parameter which determines whether the disease-free equilibrium is stable (R0<1) or unstable to perturbations that will take the system to an endemic state. This is followed by a section dedicated to the stability analysis of the disease-free equilibrium (R0>1). My first reaction to this was to say that this section is redundant given that R0 has already been calculated. Closer inspection, however, shows contradiction between the two sections. While the R0 section implies that the disease-free state loses stability when beta*(mu*p+c)/(mu+c)>(k+mu+muI), the stability analysis section concludes that this happens when p*beta>(k+mu+muI). I have not verified the calculations in full, but this cross check shows that there must be an error somewhere needing to be corrected. I think the authors will want to verify their calculation.

Minor comments:

In the abstract and other parts in the text, the authors refer to the 5 host states as “immunological states”. I don’t think that immunity is always the factor that differentiates the states. For example, the difference between “active TB” and “treated TB” is not whether individuals are immune or not, but rather whether they are under treatment or not. This can be fixed by simply using the denomination “host states”.

In page 3, 3rd paragraph, I got stuck where it reads “because of a high ‘new’ TB event frequency”. Consider saying just “because of a high TB event frequency”.

In the last sentence of the same page, the authors say that “the model includes HIV infection”. I don’t think it does!

At the end of page 5, there is a period “M. Where” where should be a comma “M, where”.

At the end of page 6, “it is likely to be greater than 1” is awkward. How about “it can be greater than 1”?

In page 7, “we assume that lambda4,5 have negative real parts”. Stability analyses do not accommodate such assumptions. Can the authors calculate the real parts of lambda4,5 and determine under what conditions (in terms of model parameters) these are negative? Can they show that these are always negative?

Figures and tables are typically displayed in the order they are cited in the text. This is not the case in this paper.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Respond or Comment

Comments on this article Comments (0)

Version 1

VERSION 1 PUBLISHED 09 Oct 2017

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 1 09 Oct 17	read	read

M. Gabriela M. Gomes, Liverpool School of Tropical Medicine, Liverpool, UK
James M. Trauer, Monash University, Melbourne, Australia

Comments on this article

All Comments(0)

Add a comment

Sign up for content alerts

Browse by related subjects

Back to all reports

Reviewer Report

15 Views

07 Feb 2018 | for Version 1

James M. Trauer, School of Public Health and Preventive Medicine, Monash University, Melbourne, Australia

15 Views Cite this report Responses(0)

Not Approved

The strengths of the manuscript by Issarow et al. include that the article is clearly written, the large majority of the mathematical results appear to be correct to me and the work does build upon previous research. Unfortunately, the main weakness is that the compartmental structure of the model fundamentally does not answer the question that has been posed.

The main reason for this is that transition from T to one of either S, L1 or L2 does not only capture a change to the relative immunity status of a person who has completed treatment, but also affects their infection status. That is, S, L1 and L2 also have different rates of endogenous reactivation to I (zero for S), as well as different rates of (re-)infection (zero for L2) and different proportions that progress to active disease immediately on infection. Therefore, the authors are really exploring the idea that treated individuals become fully susceptible and clear their infection (transition to S), behave as for once infected persons (transition to L1) or behave as for multiply infected persons (transition to L2 and remain immune from further infection) - in all respects. Perhaps it may be possible to argue that this is an exploration that is of interest and has a sound basis in epidemiology, but it is not the argument that the authors make and not the question they are seeking to answer. Also, it is unclear which of the multiple epidemiological differences differences between S, L1 and L2 is driving the observations.

Further, the reason for persons spending one year in the T compartment is unclear. If T is intended to represent persons under treatment (which is not what the authors argue) then this might be reasonable. However, in this case, the sojourn time in T should probably be six months, the alpha parameter should better represent relapse rates (and so be greater than 1% for Cape Town). Therefore, it is unclear what this state represents, other than that patients are fully immune from reinfection during their stay in T and are waiting to transition to a new susceptibility state.

The result for the basic reproductive number is doubtless correct and the method used to obtain it is well accepted. However, the formula can be calculated much more easily by simply taking the product of the number of infections per unit time in I (beta), the duration of time in I (1 / (k + mut + mu)) and the proportion of infections reaching I (which requires a small amount of algebra only). Similarly, stability analysis for the disease free equilibrium seems correct (although the calculations are a little beyond my mathematical ability), but there is no reason to doubt that the disease-free equilibrium would be stable. (Finding a second equilibrium at R0=1 and hence a backward bifurcation might perhaps be of more interest - however, as omega remains < 1 throughout the calculations, I do not believe such a phenomenon would be present.)

I have suggested reject as a decision for this manuscript, but am on the borderline between reject and major revision. I have also read the other reviewer's comments, which would also strengthen the paper and note her suggestion for a major revision. Therefore, I would be happy to review another version of the manuscript if the editors feel this is appropriate.

MINOR COMMENTS
Value of k for case detection is set at 0.68/year, but rationale is not described. Presumably this is the 2014 CDR estimate for South Africa. However, CDR is a proportion, so it cannot be simply incorporated into the model as a rate.
In the Methods it is stated that susceptible individuals have never been previously infected and L1 compartment individuals have only been infected once - however, this is only true if g=r=0, which is only the case in one configuration that is explored. Therefore these statements are misleading.
Prefer high-burden to high-burdened
Space between y and r-1 is unclear, should be just yr-1
Definitions of the transmission and transition matrices are unclear and seem incorrect.
Prefer lower limit of vertical axis of Figure 3 to be zero.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

No

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Tuberculosis, modelling, respiratory infections

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

14 Views

05 Feb 2018 | for Version 1

M. Gabriela M. Gomes, Liverpool School of Tropical Medicine, Liverpool, UK

14 Views Cite this report Responses(0)

Approved With Reservations

This paper presents a mathematical model for the transmission of tuberculosis in human populations, and describes how endemic equilibria change with effective contact rate and post treatment immune status.

The novelty of the model is the way in which the latent infection compartment is slip into L1 and L2. The primary infection compartment (L1) consists of individuals who have been infected from a susceptible TB-free state (S) and were able to contain the infection in a latent state. These individuals are subject to reactivation and progression to active disease at a rate 0.0026 per year, and to reinfection at a rate 0.21 times the force of infection, where 0.21 accounts for reduced susceptibility due to prior infection. The reinfection compartment (L2) consists of those individuals who have been reinfected from L1 and were again able to contain the infection in a latent state. These individuals are now subject to reactivation and progression to active disease at an increased rate 0.0053 per year, but are no longer susceptible to subsequent reinfections. The model also provides the option for individuals who had active TB disease to return to S, L1 or L2 upon successful treatment. This seems sensible to me and so do the results, although I have not seen TB transmission models formulated in exactly this way before.

After defining the model, the authors proceed to calculating the basic reproduction number R0, the threshold parameter which determines whether the disease-free equilibrium is stable (R0<1) or unstable to perturbations that will take the system to an endemic state. This is followed by a section dedicated to the stability analysis of the disease-free equilibrium (R0>1). My first reaction to this was to say that this section is redundant given that R0 has already been calculated. Closer inspection, however, shows contradiction between the two sections. While the R0 section implies that the disease-free state loses stability when beta*(mu*p+c)/(mu+c)>(k+mu+muI), the stability analysis section concludes that this happens when p*beta>(k+mu+muI). I have not verified the calculations in full, but this cross check shows that there must be an error somewhere needing to be corrected. I think the authors will want to verify their calculation.

Minor comments:

In the abstract and other parts in the text, the authors refer to the 5 host states as “immunological states”. I don’t think that immunity is always the factor that differentiates the states. For example, the difference between “active TB” and “treated TB” is not whether individuals are immune or not, but rather whether they are under treatment or not. This can be fixed by simply using the denomination “host states”.

In page 3, 3rd paragraph, I got stuck where it reads “because of a high ‘new’ TB event frequency”. Consider saying just “because of a high TB event frequency”.

In the last sentence of the same page, the authors say that “the model includes HIV infection”. I don’t think it does!

At the end of page 5, there is a period “M. Where” where should be a comma “M, where”.

At the end of page 6, “it is likely to be greater than 1” is awkward. How about “it can be greater than 1”?

In page 7, “we assume that lambda4,5 have negative real parts”. Stability analyses do not accommodate such assumptions. Can the authors calculate the real parts of lambda4,5 and determine under what conditions (in terms of model parameters) these are negative? Can they show that these are always negative?

Figures and tables are typically displayed in the order they are cited in the text. This is not the case in this paper.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

No source data required
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

[1] 1. Andrews JR, Morrow C, Walensky RP, et al.: Integrating social contact and environmental data in evaluating tuberculosis transmission in a South African township. J Infect Dis. 2014; 210(4): 597–603. PubMed Abstract | Publisher Full Text | Free Full Text

[2] 2. Wood R, Morrow C, Ginsberg S, et al.: Quantification of Shared Air: A Social and Environmental Determinant of Airborne Disease Transmission. PLoS One. 2014; 9(9): e106622. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Nyabadza F, Winkler D: A simulation age-specific tuberculosis model for the Cape Town metropole. S Afr J Sci. 2013; 109(910): 1–7. Publisher Full Text

[4] 4. Vynnycky E, Fine PE: The natural history of tuberculosis: the implications of age-dependent risks of disease and the role of reinfection. Epidemiol Infect. 1997; 119(2): 183–201. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Gabriela M Gomes M, Rodrigues P, Hilker FM, et al.: Implications of partial immunity on the prospects for tuberculosis control by post-exposure interventions. J Theor Biol. 2007; 248(4): 608–617. PubMed Abstract | Publisher Full Text

[6] 6. Cohen T, Colijn C, Finklea B, et al.: Exogenous re-infection and the dynamics of tuberculosis epidemics: local effects in a network model of transmission. J R Soc Interface. 2007; 4(14): 523–531. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Middelkoop K, Bekker LG, Shashkina E, et al.: Retreatment tuberculosis in a South African community: the role of re-infection, HIV and antiretroviral treatment. Int J Tuberc Lung Dis. 2012; 16(11): 1510–1516. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Andrews JR, Noubary F, Walensky RP, et al.: Risk of progression to active tuberculosis following reinfection with Mycobacterium tuberculosis. Clin Infect Dis. 2012; 54(6): 784–791. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Fletcher HA, Schrager L: TB vaccine development and the End TB Strategy: importance and current status. Trans R Soc Trop Med Hyg. 2016; 110(4): 212–218. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Johnstone-Robertson S, Lawn SD, Welte A, et al.: Tuberculosis in a South African prison - a transmission modelling analysis. S Afr Med J. 2011; 101(11): 809–813. PubMed Abstract | Free Full Text

[11] 11. Hermans S, Horsburgh CR Jr, Wood R: A Century of Tuberculosis Epidemiology in the Northern and Southern Hemisphere: The Differential Impact of Control Interventions. PLoS One. 2015; 10(8): e0135179. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Gomes MG, Franco AO, Gomes MC, et al.: The reinfection threshold promotes variability in tuberculosis epidemiology and vaccine efficacy. Proc Biol Sci. 2004; 271(1539): 617–623. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Verver S, Warren RM, Beyers N, et al.: Rate of reinfection tuberculosis after successful treatment is higher than rate of new tuberculosis. Am J Respir Crit Care Med. 2005; 171(12): 1430–1435. PubMed Abstract | Publisher Full Text

[14] 14. Dye C, Gamett GP, Sleeman K, et al.: Prospects for global tuberculosis control under the WHO dots strategy. Distr: General WHO/TB 98.251. 1998. Reference Source

[15] 15. Fennelly KP, Jones-López EC: Quantity and quality of inhaled dose predicts immunopathology in tuberculosis. Front Immunol. 2015; 6: 313. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Blower SM, Mclean AR, Porco TC, et al.: The intrinsic transmission dynamics of tuberculosis epidemics. Nat Med. 1995; 1(8): 815–821. PubMed Abstract | Publisher Full Text

[17] 17. Sanchez MA, Blower SM: Uncertainty and sensitivity analysis of the basic reproductive rate. Tuberculosis as an example. Am J Epidemiol. 1997; 145(12): 1127–1137. PubMed Abstract | Publisher Full Text

[18] 18. South Africa Demographics Profile. 2014.

[19] 19. World Health Organization: Global tuberculosis report. 2015. Reference Source

[20] 20. van den Driessche P, Watmough J: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002; 180(1–2): 29–48. PubMed Abstract | Publisher Full Text

[21] 21. Diekmann O, Heesterbeek JA, Roberts MG: The construction of next-generation matrices for compartmental epidemic models. J R Soc Interface. 2010; 7(47): 873–885. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Kranzer K, Houben RM, Glynn JR, et al.: Yield of HIV-associated tuberculosis during intensified case finding in resource-limited settings: a systematic review and meta-analysis. Lancet Infect Dis. 2010; 10(2): 93–102. PubMed Abstract | Publisher Full Text | Free Full Text

[23] 23. Comstock GW, Baum C, Snider DE Jr: Isoniazid prophylaxis among Alaskan Eskimos: a final report of the bethel isoniazid studies. Am Rev Respir Dis. 1979; 119(5): 827–830. PubMed Abstract

Impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease using a mathematical model

Abstract

Keywords

Introduction

Methods

Model design and development

Model description and assumptions

Figure 1. TB transmission model to study the impact of effective contact rate and post treatment immune status on population tuberculosis infection and disease.

Table 1. Description of parameters used in Figure 1.

Basic reproduction number

Stability analysis of the disease free equilibrium

Results from numerical analysis

Figure 2. Numerical simulation of Equation (1) when all treated individuals move to a newly infected state from β = 5 to β = 30 y r–1.

Table 2. Comparison of the number of individuals in all five states at stability point of a TB epidemic, when all treated individuals move to a newly infected state with increasing effective contact rate (Figure 2).

Table 3. Comparison of the number of individuals in all five states at stability point of a TB epidemic, when all treated individuals move to a reinfected state with increasing effective contact rate (Figure 4).

Table 4. Comparison of the number of individuals in all five states at stability point of a TB epidemic, when all treated individuals move to a susceptible state (Figure 5).

Figure 3. Separation and comparison of new infection and reactivation active TB cases when all treated individuals (T) move to a susceptible (S), newly infected (L1) or reinfected state (L2).

Figure 4. Numerical simulation of Equation (1) when all treated individuals move to a reinfected state from β = 5 to β = 30 y r−1.

Figure 5. Numerical simulation of a mathematical model (Equation (1)) to explore the impact of effective contact rate (β) varying from 5 to 30 yr−1 among 100, 000 completely susceptible individuals, when all treated move to a susceptible state.

Figure 6. Comparison of active TB cases when all treated individuals (T) move to either a susceptible (S), newly infected (L1) or reinfected state (L2) at stability point of a TB epidemic (Table 2–Table 4).

Figure 7. Number of individuals per 100, 000 when all treated individuals move to a newly infected state with increasing effective contact rate from 5 to 30 y r–1 (Table 2).

Figure 8. Number of individuals per 100, 000 when all treated individuals move to a reinfected state with increasing effective contact rate from 5 to 30 y r–1 (Table 3).

Figure 9. Number of individuals per 100, 000 when all treated individuals move to a susceptible state with increasing effective contact rate from 5 to 30 y r–1 (Table 4).

Discussion

Data availability

Competing interests

Grant information

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 2. Numerical simulation of Equation (1) when all treated individuals move to a newly infected state from β = 5 to β = 30 y r^–1.

Figure 3. Separation and comparison of new infection and reactivation active TB cases when all treated individuals (T) move to a susceptible (S), newly infected (L₁) or reinfected state (L₂).

Figure 4. Numerical simulation of Equation (1) when all treated individuals move to a reinfected state from β = 5 to β = 30 y r⁻¹.

Figure 5. Numerical simulation of a mathematical model (Equation (1)) to explore the impact of effective contact rate (β) varying from 5 to 30 yr⁻¹ among 100, 000 completely susceptible individuals, when all treated move to a susceptible state.

Figure 6. Comparison of active TB cases when all treated individuals (T) move to either a susceptible (S), newly infected (L₁) or reinfected state (L₂) at stability point of a TB epidemic (Table 2–Table 4).

Figure 7. Number of individuals per 100, 000 when all treated individuals move to a newly infected state with increasing effective contact rate from 5 to 30 y r^–1 (Table 2).

Figure 8. Number of individuals per 100, 000 when all treated individuals move to a reinfected state with increasing effective contact rate from 5 to 30 y r^–1 (Table 3).

Figure 9. Number of individuals per 100, 000 when all treated individuals move to a susceptible state with increasing effective contact rate from 5 to 30 y r^–1 (Table 4).