Keywords
Biochemical circuit, Hill equation, synthetic biology, systems biology, aggregation, robustness
Biochemical circuit, Hill equation, synthetic biology, systems biology, aggregation, robustness
This version adds two new figures to show how the logarithmic sensor responds for various parameter combinations.
See the author's detailed response to the review by Sudin Bhattacharya
See the author's detailed response to the review by Marco Archetti
I present a simple biochemical circuit that logarithmically transforms input signals. This circuit adds the outputs of several reactions that follow standard mass action Michaelis-Menten kinetics. Alternatively, the biochemical kinetics may follow the commonly observed Hill equation response, which includes Michaelis-Menten kinetics as a special case. This sensor has high dynamic range, responding logarithmically across many orders of magnitude. The high dynamic range is achieved by adding together reactions with different sensitivity ranges. The aggregate nature of this circuit provides robustness to parameter variations. Aggregate sensor design may explain the commonly observed high dynamic range of logarithmic biological responses and may also provide a useful tool for synthetic biology.
Many biochemical reactions and cellular responses transform an input, x, into an output, y, according to the Hill equation
in which c is the value of the input x that yields one-half of the maximal output response, k is the Hill coefficient that determines the shape of the response, and y is normalized to be between 0 and 11. Simple mass action kinetics often follows the Hill equation with k = 1, which corresponds to classical Michaelis-Menten kinetics2. For example, the input may drive production of the output, and the output may spontaneously transform back to a prior state.The output of the Hill equation scales approximately logarithmically with its input through the middle part of its response range, because y is roughly linear with respect to log x. Prior studies have emphasized that a Hill equation response can act as a logarithmic sensor3,4. However, a single Hill equation response provides a logarithmic sensor with limited dynamic range (Figure 1A).
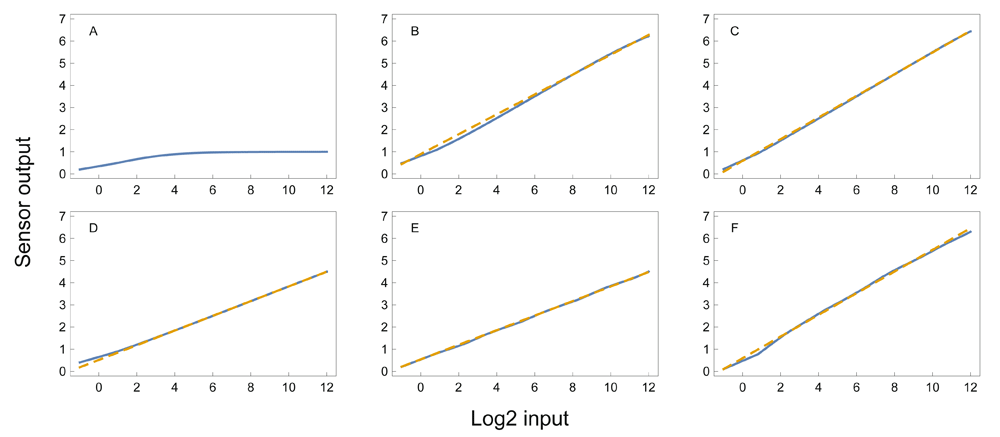
Each unit on the input scale corresponds to a doubling of the input. The range of 13 doublings is approximately four orders of magnitude, 213 ≈ 104. A logarithmic sensor responds linearly with respect to the logarithm of the input. The solid blue lines show the response, y, from Equation 1. The dashed gold lines are linear fits to the response. (A) A single Hill equation with c = 1 and k = 2. A linear response with low sensitivity occurs over a few doublings at small input levels. The following plots all use n = 7 and additional parameters as described from the summed Hill equation in Equation 1, in which ci = bi. (B) Response with k = 1 and b = 4. (C) Response with k = 2 and b = 4. (D) Response with k = 1 and b = 8. (E) Response with k = 2 and b = 8. (F) Same average parameters values of k = 2 and ci = bi for b = 4 as in the plot above, but with random parameter fluctuations around those average values. For each of the 7 Hill equations in the sum given in Equation 1, each parameter was obtained by a different random number drawn from a normal distribution. For each k, the parameters were drawn from a normal distribution with mean 2 and standard deviation 2 × 0.25 = 0.5. For each ci, the parameters were drawn from a normal distribution with mean 4i and standard deviation 4i ×0.25. The response remains nearly linear in spite of the random parameter fluctuations (see Data availability).
My extended dynamic range sensor arises by adding together n Hill equations with increasing values of the half-maximal response, ci, as
For example, if ci = bi, then each reaction in the sum has an increasing input value at which its maximal sensitivity occurs. Figure 1B–E shows that simple combinations of k and b create a logarithmic sensor, in which the output is linearly related to the logarithm of the input. The logarithmic relation holds robustly when the parameters k and b of the individual reactions vary stochastically (Figure 1F). Figure 2 and Figure 3 show the response for various parameter combinations.
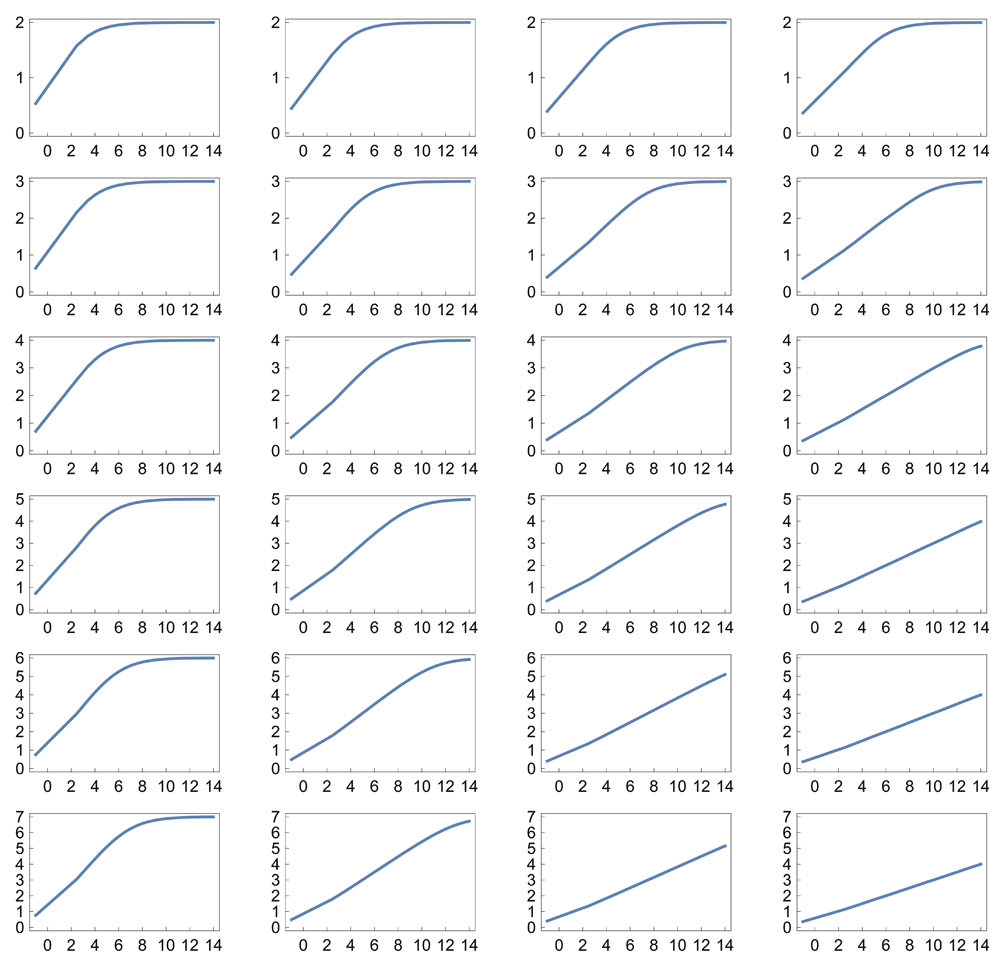
Note that the scale along the x-axis is increased to 214 compared with 212 in Figure 1. All plots use the Michaelis-Menten relation with Hill equation coefficient k = 1 (see Data availability).
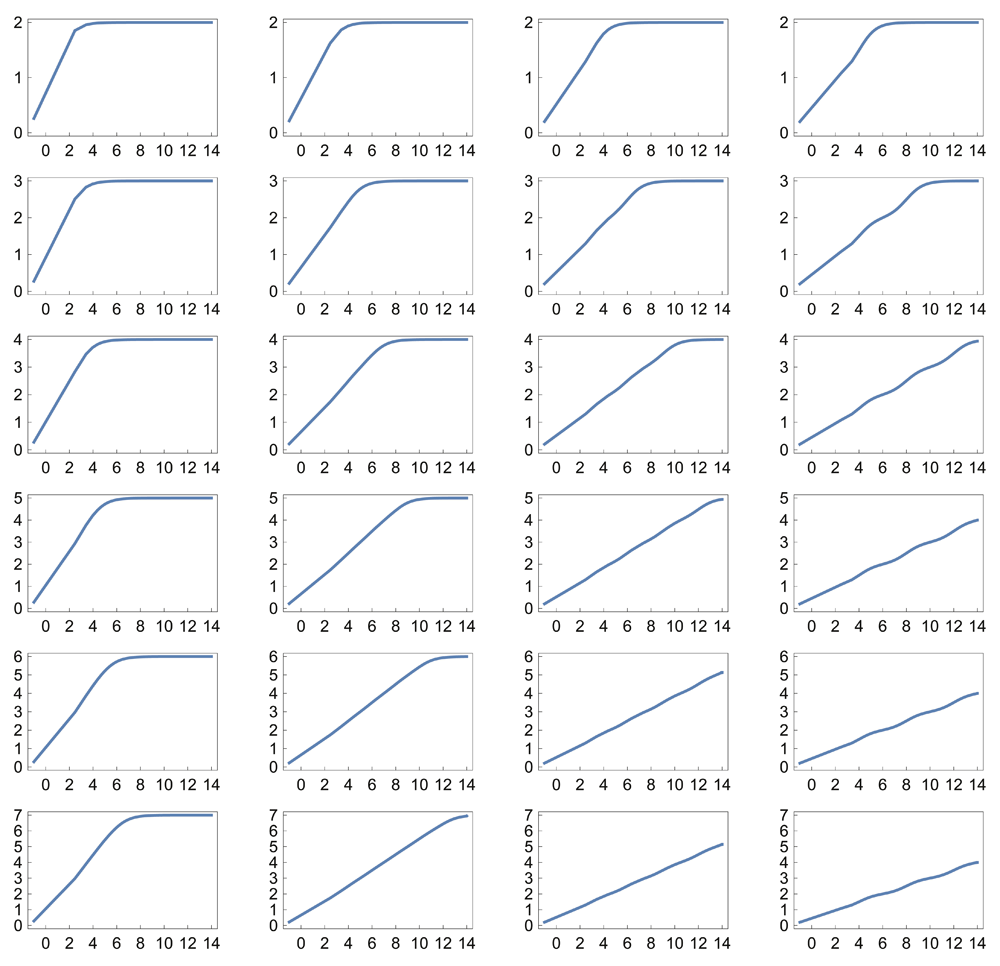
Several biochemical circuit responses and many aspects of perception scale logarithmically5. A robust and generic pattern of this sort seems likely to depend on a robust and generic underlying design. In the search for a generic circuit, my biochemical logarithmic sensor has three advantages over prior designs. First, prior models depended on particular molecular assumptions about biochemical kinetics or reaction pathways3,4. My design requires only Michaelis-Menten or Hill equation responses, which are very widely observed in biochemical and cellular systems1. Second, prior models focused on single input-output processes, which have relatively narrow dynamic range. My aggregate design provides a logarithmic response over a vastly greater range. Third, the prior models’ responses are easily perturbed by parameter fluctuations. My design performs robustly with respect to broad fluctuations in parameters. The robustness of my logarithmic sensor emphasizes the potential to achieve precise response characteristics from underlying sloppy components when using an aggregate design6,7.
Mathematica source code to produce Figure 1 can be found at: https://doi.org/10.5281/zenodo.12176588
License: CC BY 4.0
National Science Foundation grant DEB–1251035 supports my research.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
Yes
Are sufficient details of methods and analysis provided to allow replication by others?
Yes
If applicable, is the statistical analysis and its interpretation appropriate?
Not applicable
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
Yes
Competing Interests: No competing interests were disclosed.
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Computational biology and toxicology
Is the work clearly and accurately presented and does it cite the current literature?
Yes
Is the study design appropriate and is the work technically sound?
No
Are sufficient details of methods and analysis provided to allow replication by others?
Partly
If applicable, is the statistical analysis and its interpretation appropriate?
Partly
Are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions drawn adequately supported by the results?
No
References
1. Huang CY, Ferrel JE: Ultrasensitivity in the mitogen-activated protein kinase cascade. Proceedings of the National Academy of Sciences. 1996; 93: 10078-10083Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Computational biology and toxicology
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 3 (revision) 18 Apr 18 |
||
|
Version 2 (revision) 23 Mar 18 |
read | read |
|
Version 1 16 Feb 18 |
read | |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)