Challenges in the use of atomistic simulations to predict solubilities of drug-like molecules

Guilherme Duarte Ramos Matos; David L. Mobley

doi:10.12688/f1000research.14960.1

Home Browse Challenges in the use of atomistic simulations to predict solubilities...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Challenges in the use of atomistic simulations to predict solubilities of drug-like molecules

[version 1; peer review: 2 approved]

Guilherme Duarte Ramos Matos¹, David L. Mobley ^1,2

PUBLISHED 31 May 2018

Author details Author details

¹ Department of Chemistry, University of California, Irvine, Irvine, California, USA
² Departments of Pharmaceutical Sciences and Chemistry, University of California, Irvine, Irvine, California, USA

Guilherme Duarte Ramos Matos
Roles: Conceptualization, Data Curation, Investigation, Methodology, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

David L. Mobley
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Cheminformatics gateway.

This article is included in the Mathematical, Physical, and Computational Sciences collection.

Abstract

Background: Solubility is a physical property of high importance to the pharmaceutical industry, the prediction of which for potential drugs has so far been a hard task. We attempted to predict the solubility of acetylsalicylic acid (ASA) by estimating the absolute chemical potentials of its most stable polymorph and of solutions with different concentrations of the drug molecule.
Methods: Chemical potentials were estimated from all-atom molecular dynamics simulations.
We used the Einstein molecule method (EMM) to predict the absolute chemical potential of the solid and solvation free energy calculations to predict the excess chemical potentials of the liquid-phase systems.
Results: Reliable estimations of the chemical potentials for the solid and for a single ASA molecule using the EMM required an extremely large number of intermediate states for the free energy calculations, meaning that the calculations were extremely demanding computationally. Despite the computational cost, however, the computed value did not agree well with the experimental value, potentially due to limitations with the underlying energy model. Perhaps better values could be obtained with a better energy model; however, it seems likely computational cost may remain a limiting factor for use of this particular approach to solubility estimation.
Conclusions: Solubility prediction of drug-like solids remains computationally challenging, and it appears that both the underlying energy model and the computational approach applied may need improvement before the approach is suitable for routine use.

Keywords

solubility, molecular crystals, free energy calculations, chemical potentials, solvation

Corresponding author: David L. Mobley

Competing interests: D.L.M. is a member of the Scientific Advisory Board for OpenEye Scientific Software.

Grant information: D.L.M. and G.D.R.M. appreciate the financial support from the National Science Foundation (CHE 1352608), and computing support from the UCI GreenPlanet cluster, supported in part by NSF Grant CHE-0840513. G.D.R.M. appreciates support from the Brazilian agency CAPES - Science without Borders program (BEX 3932-13-3).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2018 Duarte Ramos Matos G and Mobley DL. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Duarte Ramos Matos G and Mobley DL. Challenges in the use of atomistic simulations to predict solubilities of drug-like molecules [version 1; peer review: 2 approved]. F1000Research 2018, 7:686 (https://doi.org/10.12688/f1000research.14960.1) First published: 31 May 2018, 7:686 (https://doi.org/10.12688/f1000research.14960.1) Latest published: 04 Jan 2019, 7:686 (https://doi.org/10.12688/f1000research.14960.2)

Introduction

Solubility is a critical property for pharmaceutical drug discovery; problems with solubility can frustrate drug discovery efforts and prevent treatments from working. The bioavailability of a drug depends on the solubility difference between different crystal structures (polymorphs), dose, drug permeability and formulation¹, so solubility plays a key role. Solubility problems can be unexpected and can pose crucial obstacles that even threaten the administration of care. For example, a well-documented case occurred in the late 1990s, when ritonavir, an HIV-protease inhibitor marketed as Norvir, failed dissolution requirements². Since ritonavir is not bioavailable in its solid form, it was administrated in capsules containing solutions designed not to be saturated with respect to the originally known molecular crystal (form I)². The newly identified polymorph, form II, was unusually stable and unusually hard to crystallize; the preparation protocol of Norvir was inadequate to make capsules from the new polymorph, which severely threatened the supply of the drug in the market and endangered the lives of many HIV-poaitive patients². Considerable effort has already been devoted to the methods to predict crystal polymorphs^3–9, but much less attention has been given to methods to predict solubilities, with or without likely polymorphs as input.

Due to the importance of aqueous solubilities in different industrial processes and environmental applications, a scientific challenge, consisting of the prediction of 32 solubilities given a database of 100 reliable measurements^10,11, was created with the goal of comparing the outcomes of different solubility prediction techniques. Participants employed methods such as artificial neural networks¹², quantitative structure-property relationship (QSPR)¹³, and deep learning¹⁴ to predict the aqueous solubilities of drug-like molecules. All of the employed methods were empirical and trained on existing measurements. The limitation of these methods, however, is the dependence of a training set of data that limits their applicability to compounds similar to those in the training of the set and impairs its transferability.

Some newer methods attempt to predict solubilities based on a physical description of the interactions in solution and in the solid state, yielding results that are in principle rigorous given an accurate energy model and an adequate method. In these approaches, molecular systems are described using force fields, i.e, potential energy functions that contain parameters describing bonds, atoms, electrostatic and non-electrostatic interactions. Molecular dynamics or Monte Carlo simulations are commonly used to sample different configurations of the system described by an energy model called a force field. The simulations then allow the estimation of physical properties, such as internal energy, free energy, and enthalpy, under different conditions. The quality of the results of such methods depends on how well the force field describes the system under study and how good the sampling method is. Thus, some researchers have recently estimated aqueous solubilities using simulations of thermodynamic cycles encompassing the crystal, the ideal gas, and an infinitely dilute solution of a given molecule^15,16. When the structure of the solid is unknown, some studies have substituted simulations of solid melts in place of a structure of the solid^17–20.

While these physical methods for predicting solubilities have received some attention in the literature, most are still in their infancy, with only a handful of studies applying them, and it is not yet clear how broadly applicable they will be^17–20, and others have only been suggested or demonstrated in proof-of-principle tests^16,21–23. Our view is that the time is ripe for physical methods to predict solubility, especially given the routine nature of solvation free energy calculations at present^24–29, which comprise essentially half of the solubility problem (see the Theory section). Polymorph and crystal structure prediction successes also mean that we may often have a suitable crystal structure of the compound as an input^{3–5,8,9,30–35}, so what remains is to predict the solubility given a crystal structure and simulations of the relevant phases.

Here, we focus on adapting and testing an existing approach for solubility prediction in the hope that it will prove to be a generally applicable method for solubility prediction that can be applied routinely. This method uses all-atom molecular dynamics simulations to estimate absolute chemical potentials and predict aqueous solubilities of molecular solids, given the crystal structure (or an estimate thereof) as input.

Theory

The solubility of a molecular solid is related to the chemical potentials of each phase

Solubility is defined as the maximum concentration of solute that can be dissolved in a selected bulk solvent. Chemical potentials (µ) of the solid-state solute and the solution are by definition equal at the solubility point, when the solution is in equilibrium with the solid.

μ_{s o l u t e}^{s o l i d} = μ_{s o l u t e}^{s o l u t i o n} (1)

Solid particles precipitate in concentrations higher than the solubility point because the solid phase becomes more stable in these conditions. In principle, we can predict at which concentration a molecule precipitates in solution if we calculate the chemical potentials of the components:

μ_{i} = {(\frac{\partial A}{\partial N_{i}})}_{V, T, N_{j, j \neq i}} = {(\frac{\partial G}{\partial N_{i}})}_{P, T, N_{j, j \neq i}} (2)

where µ_i is the chemical potential of component i; A is the Helmholtz free energy; G is the Gibbs free energy; N_{j, j≠i} is the number of molecules of each component in the mixture; V is the volume of the system; T its temperature; and P its pressure. Calculations from systems under a constant V and T yield A; G is obtained from simulations under constant P and T conditions. In order to estimate the chemical potential of one component in solution and in its molecular solid, however, we need to know the absolute free energy of the system in these states. We calculated absolute free energies using alchemical free energy calculations.

Alchemical free energy calculations can be used to calculate absolute free energies

The absolute free energy of a system can be determined if we know its partition function (Q), a function that connects microscopic properties of the system with macroscopic thermodynamic quantities. Unfortunately, it is very hard to calculate the absolute free energy of real systems because we don’t know their partition functions. Free energy calculations allow us to bypass this problem, but require at least two states: a reference state whose free energy can be analytically or numerically found, and a final state of interest^36,37. We chose to calculate the free energy difference using alchemical free energy calculations, a method in which we simulate a series of non-physical intermediates between the end states³⁸.

Each intermediate state in the alchemical path is described by a Hamiltonian ℋ (q, p; λ), i.e, the energy of the state as a function of atomic positions (q), momenta (p) and a coupling parameter (λ):

ℋ (q, p; λ) = f (λ) ℋ_{i n i t i a l} (q, p; λ) + g (λ) ℋ_{f i n a l} (q, p; λ) (3)

where ℋ_initial and ℋ_final respectively are the Hamiltonians of the initial and the final state; and f (λ) and g(λ) are functions used to mix the Hamiltonians, and are usually set such that ℋ = ℋ_initial at λ = 0 and ℋ = ℋ_final at λ = 1.

A variety of different estimators can be used to analyze alchemical free energy calculations, and have different strengths and weaknesses, as well as different data requirements. Here, we employ several different estimators we introduce briefly in the following.

One way to calculate the free energy difference (∆A) between the end states is Thermodynamic Integration (TI)³⁹:

Δ A = {\int_{λ = 0}^{λ = 1} 〈 \frac{\partial ℋ}{\partial λ} 〉}_{λ} d λ (4)

in which a set of discrete λ values correspond to states along the alchemical path. 〈〉 means that we are have to calculate the ensemble average of the derivative between the brackets. TI performs as well as more efficient methods if the integrand is smooth, but breaks down if this condition is not satisfied^40–42.

An alternate free energy estimation method computes ∆A directly via:

Δ A = - \frac{1}{β} ln {〈 e^{- β [ℋ_{f i n a l} - ℋ_{i n i t i a l}]} 〉}_{i n i t i a l} (5)

where the ensemble average is calculated over the configurations of the initial state, and β is the reciprocal of k_BT, the product between the Boltzmann constant and the absolute temperature. We call this approach exponential averaging⁴³ (EXP).

Most free energy calculations involve many intermediates associated with the coupling parameter (λ), allowing simulation of intermediate states in between the two end states of interest. The free energy change between the end points of a path defined by N intermediates is:

Δ A = \sum_{n = 1}^{N - 1} Δ A_{n \to n + 1} (6)

where ∆A_n→n+1 is the free energy difference between (n+1)-th and the n-th intermediate states. Equation 5 can be used to calculate the free energy difference between each adjacent pair of states and yields the exact result at the limit of very large samples, but it is inefficient for most applications³⁸.

The Bennett acceptance ratio⁴⁴ (BAR) provides an estimator that is superior for most purposes. It calculates the free energy difference between the n-th and the (n + 1)-th states from the following relationship:

{〈 \frac{1}{1 + \frac{N_{n}}{N_{n + 1}} e^{β (Δ ℋ_{n \to n + 1} - Δ A)}} 〉}_{n} = {〈 \frac{1}{1 + \frac{N_{n + 1}}{N_{n}} e^{β (Δ ℋ_{n + 1 \to n} + Δ A)}} 〉}_{n + 1} (7)

where N_n and N_n+1 are the number of statistically independent samples in states n and n + 1, respectively, and ∆ℋ_n→n+1 = −∆ℋ_n+1→n are the Hamiltonian differences between n and n + 1. BAR is more efficient than EXP^45,46 and minimizes the free energy uncertainty⁴⁴. Multistate Bennett acceptance ratio⁴¹ (MBAR) is an extension of BAR that takes in consideration the degree of configuration space overlap between a given state and all other states in the transformation, whereas BAR only uses the information of neighboring states. MBAR and BAR perform similarly when the spacing between the intermediate states is moderate, but MBAR is the most well-performing free energy estimator⁴².

The absolute free energy of a solid is calculated using an ideal system as reference

In this work, we seek to predict the solubilities of molecular solids. Part of this problem requires predicting the free energy or chemical potential of the solid. One way this has been attempted in the past is via the Einstein crystal method (ECM), which calculates the absolute free energy of a solid using an Einstein crystal as a reference state. In this method, the crystal lattice is made of atoms restrained to their positions by a harmonic potential; additionally, the center of mass of the system is held fixed⁴⁷.

In the ECM, and in this work, the absolute free energy of the molecular solid is found by designing a path where force field terms are progressively turned on, and the harmonic potential position restraints are turned off. The fixed center of mass is important to avoid a quasi-divergence issue when calculating the free energy term of releasing the system from the harmonic position restraints, but the contribution of the fixed center of mass needs to be included in the cycle to obtain the correct absolute free energy for the system (Figure 1(a))^47–49.

Figure 1.

(a) Thermodynamic cycle representing the Einstein Crystal Method. (b) Thermodynamic cycle representing the Einstein molecule method (EMM). Note that the EMM requires only two free energy calculations despite being a bigger thermodynamic cycle. The canceling terms in (b) correspond to the free energies of fixing and releasing one atom in the crystal lattice⁴⁸.

In ECM, the free energy is calculated by:

A^{s o l i d} = A_{F C M}^{E C} + Δ A_{E C \to I E C} + Δ A_{I E C \to S F C M} + Δ A_{r e l e a s e C M} (8)

where $A_{F C M}^{E C}$ is the free energy of the Einstein crystal (EC) with a fixed center of mass (FCM); ∆A_EC→IEC is the free energy difference between the Einstein crystal (EC) and the interacting Einstein crystal (IEC), i.e., the free energy difference in a transformation where the force field is progressively turned on throughout the calculation path. ∆A_IEC→SFCM is the free energy difference between the IEC and the solid with a fixed center of mass (SFCM), i.e, turning off the harmonic restraints; and ∆A_{release CM} is the free energy of release of the center of mass (CM).

ECM can be difficult to implement because of the need for a fixed center of mass, so our work here is based on an alternative approach that is easier to implement. When particles move in ECM, the lattice needs to be moved because the center of mass is fixed^47,48,50. Our method of choice, the Einstein Molecule Method (EMM, see Figure 1(b)), fixes a single atom in the lattice instead of the center of mass and is more easily implemented than ECM because of the relative difficulty of introducing center of mass restraints into existing simulation packages^{22,48,50–52}. EMM has been used to predict phase diagrams of TIP4P and SPC/E water models⁴⁸, free energies of ice polymorphs, solid methanol and toy systems^49,52, and the solubilities of potassium and sodium chlorides^22,51.

In EMM, the free energy of a solid is:

A^solid = A^EM+∆A_EM→IEM+∆A_IEM→solid (9)

where A^EM is the free energy of the ideal Einstein molecule; ∆A_id→IEM is the free energy difference between the ideal Einstein molecule and the interacting Einstein molecule (i.e, turning on the force field); and ∆A_IEM→solid is the free energy difference between the interacting Einstein molecule and the solid (i.e, turning off the harmonic restraints). The advantage of EMM over ECM is the absence of the need to calculate a free energy term associated with releasing the fixed reference point⁴⁸.

Here, as per Equation 9, we compute the free energy of the solid by combining the absolute free energy of the ideal Einstein molecule with two terms that we calculate via alchemical free energy calculations—∆A_EM→IEM and ∆A_IEM→solid; these involve alchemically changing the interactions in the system. Numerical integration of Equation 10 allows the calculation of the ideal term, A^EM⁵²:

$A^{E M} = - \frac{1}{β} ln Q_{E M} = \frac{1}{β} ln \frac{N Λ^{3}}{V} - \frac{1}{β} ln \int e^{- β U_{E M, 1} (Ω_{1}) d Ω_{1}} - \frac{(N - 1)}{β} ln \int \frac{1}{Λ^{3}} e^{- β U_{E M, 2} (r_{2}, Ω_{2}) d r_{2} d Ω_{2}} (10)$

where A^EM and Q_EM are the free energy of the Einstein molecule and its partition function; U_EM,1(Ω₁) is the potential energy of the fixed particle 1; U_EM,2(r₂Ω₂) is the potential energy of a non-fixed particle at a distance r₂ of particle 1; Ω₁ and Ω₂ are all the possible orientations the molecules can have in the lattice; Λ, V, N, and β respectively are the de Broglie wavelength, the system’s volume, its number of particles, and the reciprocal of k_BT, the product of the Boltzmann constant and the absolute temperature.

The chemical potential of a component of a solution can be calculated using free energy calculations

Another critical component of computing the solubility of a compound is estimating the chemical potential of a solute in solution, since the solubility point is the concentration at which the chemical potentials of compound in the two phases are equal.

The chemical potential of a component i in solution, µ_i, has an ideal and and excess component:

$μ_{i} = - \frac{1}{β} ln q_{i} + \frac{1}{β} ln \frac{Λ_{i}^{3} N_{i}}{V} - \frac{1}{β} ln {〈 e^{- β [U (N_{i} + 1) - U (N_{i})]} 〉}_{i n i t i a l} (11)$

where q_i is the internal partition function of a single molecule of the solute, U(N_i) is the potential energy of the system with N_i particles, Λ is the de Broglie thermal wavelength, and V is the system’s volume⁵³. 〈〉_initial means that the term was obtained from an ensemble average over the configurations of the initial state (see Equation 5). The first two terms of the equation above correspond to the ideal component of µ_i; the last one, $μ_{i}^{e x}$ , corresponds to the excess component of µ_i, and is associated with all non-ideal interactions of the extra component i with the solution (i.e. physical interactions that differ from those given by the ideal gas law). We obtained excess chemical potentials from solvation free energy calculations; the solute molecule is inserted in the solution by progressively turning on its interactions with the surrounding environment^24,28,54.

The challenge associated with the calculation of µ_i is the calculation of the standard chemical potential of i, $μ_{i}^{0}$ , the first term of Equation 11. q_i, the internal partition function, includes the rotation, vibrational, electronic and nuclear partition functions of a single molecule⁵³ and is unknown. Here, we found a way of calculating $μ_{i}^{0}$ without the knowledge of q_i by alchemically transforming a single solute molecule into a single Einstein molecule, whose absolute free energy we know how to calculate^48–50.

Distinctives of this work

We are aware of three main approaches to compute the solubility of solids in solution using physical approaches: ECM-based methods^21,23, EMM-based methods^22,51,55, and the approach of Michael Schnieders and collaborators which computes sublimation and solvation free energies and uses these in an alternate thermodynamic cycle to obtain solubility estimates^15,56.

Many of the applications of these approaches have been to the solubility of ionic solids, with both ECM-²¹ and EMM-based approaches^22,51,55 having some success. However, molecular solids introduce substantial additional complexities for both of these approaches.

The ECM has seen an initial test on solubility estimation. Li et al.²³ used the ECM to estimate the solubility of napthalene, but made several approximations such as assuming that the internal partition function component of the solute cancels between environments (perhaps justified given napthalene’s low solubility).

We are not aware of any work applying the EMM to solubility estimation of molecular solids; to our knowledge our work is the first to make such an attempt, though EMM has been used before to estimate the free energy of simple molecular solids^49,52 but not the solubility. This explains our need to find our own approach to estimate $μ_{i}^{0}$ for a single solute molecule.

The Schneiders approach is an orthogonal one that we do not examine here.

Methods

Systems under study

Here, we chose three systems to study: An argon crystal for some small initial tests, α-methanol to help establish our protocol, and acetylsalicylic acid (ASA) as our main object of study. ASA is a known anti-inflammatory whose most stable polymorph, form I⁵⁷, has an aqueous solubility of approximately 0.038% mole fraction at 298 K⁵⁸. We also used α-methanol at 150 K and a toy facecentered cubic (fcc) argon crystal⁵⁹ to help us find an optimal protocol to calculate the absolute free energy of a molecular solid. α-methanol was chosen because it had been used before in a study that applied the EMM to calculate the absolute free energy of the solid⁵².

All simulations were run in GROMACS 4.6.7^60–63. With one exception, all simulations used the General Amber force field (GAFF) version 1.7 with AM1-BCC charges^64,65; the exception was α-methanol, because we ran these simulations using the input files – coordinates and force field parameters – provided by Aragonès et al., who used an united atom version of the OPLS force field⁵².

We simulated all solids and liquids using 5 ns Langevin dynamics simulations. ASA, α-methanol, and argon were simulated respectively at 298.15 K, 150.0 K, and 4.0 K. Our simulations had the same length as the simulations run by Aragonès et al. All solid state simulations were run in NVT conditions. Liquid state simulations were run in NPT conditions; pressure was kept constant at 101.335 kPa using the Parrinello-Rahman barostat⁶⁶. We used the TIP3P water model⁶⁷ for all our liquid state simulations. More simulation details and example input files with full details can be found in the Supporting Information.

Calculation of the absolute free energy of molecular crystals

The absolute free energies of the solids were calculated from trajectories of simulation boxes with 64 ASA molecules, 100 OPLS methanol molecules, and 864 argon atoms with periodic boundary conditions. ASA’s unit cell was obtained from Mercury CSD 3.8⁶⁸ and the fcc argon crystal was obtained from the literature⁵⁹. Simulation box sizes were chosen to be approximately between 2 nm and 3 nm to ensure that box sizes were large enough that atoms and their periodic copies were not within cutoff distance of one another. α-methanol’s crystal was obtained from the Supporting information of Aragonès et al.⁵² We used Amber14’s ambertools^69–72 and ParmEd⁷³ to generate the ASA’s and argon’s solid state input files. All atoms but one were subjected to harmonic constraints in the x, y, and z coordinates. A single atom was kept fixed in space to act as the reference point for the calculations, as explained in the Introduction.

Monte Carlo integration yielded A_EM, the free energy of the Einstein molecule, as it was previously done for α-methanol in the literature⁵². ∆A_id→IEM and ∆A_IEM→solid were estimated using TI³⁹ and the multistate Bennett acceptance ratio (MBAR)⁷⁴. We used force constants of 4000 k_BT/Å² to restrain atoms to their lattice positions in ASA and argon simulations because it allowed us to use a reasonable time step of 1.0 fs in all simulations. α-methanol simulations used the same force constant that had been previously used by Aragonès et al.⁵².

We used alchemical free energy calculations to obtain the difference in free energy between the reference Einstein molecule and the solid. This step was divided in two parts: (a) the force field parameters are alchemically turned on, and (b) the harmonic constraints are turned off.

Here, we deviate from earlier work which calculated the absolute free energy of a solid using EMM by introducing additional intermediate states to improve accuracy, along with using a superior free energy estimator.

For the calculation of ∆A_id→IEM, we found it was crucial to introduce intermediate states; we also switched to using the MBAR estimator. The original EMM calculation of the absolute free energy of a solid^22,48–52 estimated ∆A_id→IEM using exponential averaging (EXP) with just two states: the Einstein molecule (EM) and the interacting Einstein molecule (IEM)^{21,22,48–52,55}. As EXP is known to have convergence issues and biases^38,40,41,45, we switched to the superior MBAR free energy estimator⁷⁴. Additionally, when we did so, we found that overlap of states (as measured by the overlap matrix⁷⁵) was insufficient so we created a series of intermediate states connecting both ends of the transformation.

For ∆A_IEM→solid., the original work used TI³⁹. Here, we replaced TI with MBAR as our analysis method of choice. Generally, the literature shows that TI performs as well as more efficient methods like BAR and MBAR when the integrand is smooth^38,40,41, but it is sensitive to the choice and number of intermediate states⁷⁶. MBAR is the most consistently well-performing free energy estimator⁴² and exploits the overlap between states more thoroughly than its predecessor, the Bennett Acceptance Ratio (BAR) estimator⁷⁴. Here, we chose to compare performance of MBAR and TI for calculation of ∆A_IEM→solid for ASA and α-methanol; we also applied EXP as a comparison in the latter case only.

Chemical potential calculations

The chemical potential of a pure solid is its molar free energy:

$μ = \frac{A}{N} (12)$

where N is the number of molecules in the solid, and A its Helmholtz free energy.

The chemical potential of a substance i in water is defined as the derivative of the free energy of the system with respect to the composition:

$μ_{i} = {(\frac{\partial G}{\partial N_{i}})}_{P, T, N_{H_{2} O}} (13)$

where G is the Gibbs free energy, and N_i is the number of molecules of i in solution; P, T, and N_H₂O are the pressure, absolute temperature, and number of water molecules in solution, and are kept constant in the calculation.

One important aspect to discuss is the reason why we chose to calculate the Helmholtz free energy for the solid and Gibbs free energies for each solution. Solid state simulations with position restraints required running under constant temperature and constant volume conditions due to software limitations, therefore we were able to calculate A for the solids. At constant pressure, both kinds of free energy are related by:

∆G = ∆A+ P∆V (14)

Since solids are much less susceptible to volume changes than liquids, it is reasonable to consider that P∆V is negligible and ∆G ≈ ∆A. For instance, the difference in volume between the experimental ASA crystal structure and the simulation box after a constant pressure equilibration stage is 0.14 nm³. The P∆V term – i.e., the free energy difference discounting possible structure relaxation effects – would be much smaller than the simulation error.

As we explain in more detail in the Results section, successful absolute free energy calculations for molecular solids require a pathway involving a large number of alchemical intermediate states. The calculation of the absolute free energies of α-methanol at 150 K and ASA required 600 states. Since GROMACS reads each λ until its fourth decimal place and the states need to be spaced more closely together as as the harmonic restraints are turned off (see Supporting Information), we decided to split each free energy calculation into sets of 100 states.

Liquid state simulation boxes were generated using the SolvationToolkit⁷⁷, a Python package that uses packmol⁷⁸, OpenMolTools (v0.6.7)⁷⁹ and OpenEye Python Toolkits^80–82. Excess chemical potentials were obtained with the same solvation free energy protocol used in previous studies²⁸: Starting from a fully interacting system, we progressively decouple the interactions of a single solute molecule with the remaining of the system, which allows us to calculate the free energy difference between a solute molecule in vacuum and in solution (i.e., the solvation free energy).

We also used alchemical free energy calculations using a single Einstein molecule as a reference state to estimate the standard chemical potential of a substance, $μ_{i}^{0}$ :

μ_{i}^{0} = μ_{i}^{i d e a l} - (μ_{i}^{F F o f f} + μ_{i}^{r e s t r a i n i n g}) (15)

where $μ_{i}^{F F o f f}$ and $μ_{i}^{r e s t r a i n i n g}$ respectively are the chemical potential associated with turning off the force field and chemical potential of restraining the atoms of the molecule to their lattice positions. $μ_{i}^{i d e a l}$ is calculated using the Monte Carlo integration procedure that we used to calculate A^EM to a single molecule.

Results

Chemical potential of molecular solids

The first step to predict aqueous solubilities with the aid of absolute free energy calculations was the assessment of the methodologies we chose to use. Since our method is the same one used by Aragonès et al.⁵² and we wanted to be sure that we could reproduce previous results, we ran simulations for α-methanol at 150 K and estimated the free energies of solids using MBAR. Turning off the harmonic restraints was the challenging step. Our MBAR calculation of ∆A_IEM→solid for α-methanol using 18 intermediate states yielded −18(3) k_BT, while our TI result was −18.421(5) k_BT and the literature result was −17.33(3) k_BT using 17 states⁵². The MBAR error was unusually high (3 k_BT), which is usually a signal of overlap problems or other serious concerns.

MBAR is a free energy estimation method that minimizes the free energy variance and considers the overlap between a given state and all the others in the transformation path⁴¹, which means that high uncertainties (±3k_BT) suggest the presence of problems in the transformation’s path. TI’s uncertainty estimates are much lower, but we believe that this is an artifact. Error analysis for TI simply does not work the same way and does not give insight into whether exploration of phase space is adequate, unlike MBAR. Specifically, uncertainty estimates from TI usually factor in only the uncertainty in the integrand at each sampled lambda value and could potentially also factor in the smoothness of the integrand (i.e. numerical integration error) but do nothing to factor in whether the integrand will in fact vary smoothly in between lambda points; usually no data is available on this. BAR and MBAR, in contrast, factor in information about how well the intermediate states overlap in phase space and reflect high uncertainties when phase space overlap is poor. In our experience, TI would usually suffer from similar problems if additional intermediate states were added, but uncertainties in TI typically do not reflect this, as is the case here. Thus, the high uncertainty of the MBAR value indicates a sampling/convergence problem which warrants further exploration.

To explore the high uncertainty of our MBAR free energy estimates, we examined the degree of overlap the intermediate states had with each other. Phase space overlap analysis^83–85 quantifies the probability that any given configuration of an intermediate state can be found in other states. A good rule of thumb for designing a set of free energy calculations spanning between two states is to ensure that the states along the path have significant overlap with their neighbors as shown in Figure 2. More overlap improves the quality of the MBAR free energy estimation: Figure 2b represents a set of restraining simulations where the free energy uncertainty can potentially be accurately estimated using BAR and MBAR; Figure 2a shows a case where it cannot. In our case we find that the α-methanol simulation using 18 intermediate states does not have adequate overlap (Figure 3)– specifically, the states 4 ≤ λ_i ≤ 17 do not have overlapping configurations with other states, which explains the 3 k_BT uncertainty in our MBAR estimate.

Figure 2. Phase space overlap between the states in a thermodynamic path for removing restraints with λ.

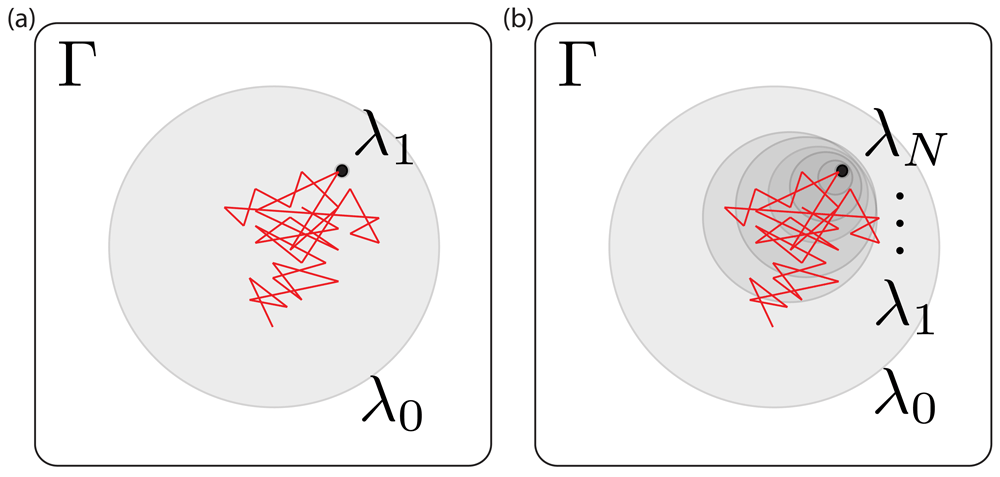
Γ represents the phase space that contains all the configurations for all the states in the path. λ₀ and λ₁ (left) or λ_N (right) represent the end states along the path, each shaded region represents a state in phase space and the red lines represent the configurations visited by the simulation run in the λ₀ state. The restrained state is a subset of the unrestrained one. (a) and (b) represent simulations with different numbers of intermediate states along the path between a fully restrained state (λ₁ (a) or λ_N (b)) and an unrestrained state (λ₀). In (a), the simulation (red) only visits very few configurations consistent with the restrained state – i.e, there is poor phase space overlap – indicating a need for more intermediate states, otherwise any free energy estimates will be subject to very high uncertainties; in (b) there is still almost no overlap between the simulation and states consistent with λ_N, but there is overlap with the next shaded region, λ₁, indicating the potential for overlap and accurate free energy estimates. Thus simulations run in each shaded region are more likely to have a bigger phase space overlap with λ_N than simulations run in λ₀.

Figure 3. Phase space overlap between the states in the path between IEM and the α-methanol solid.

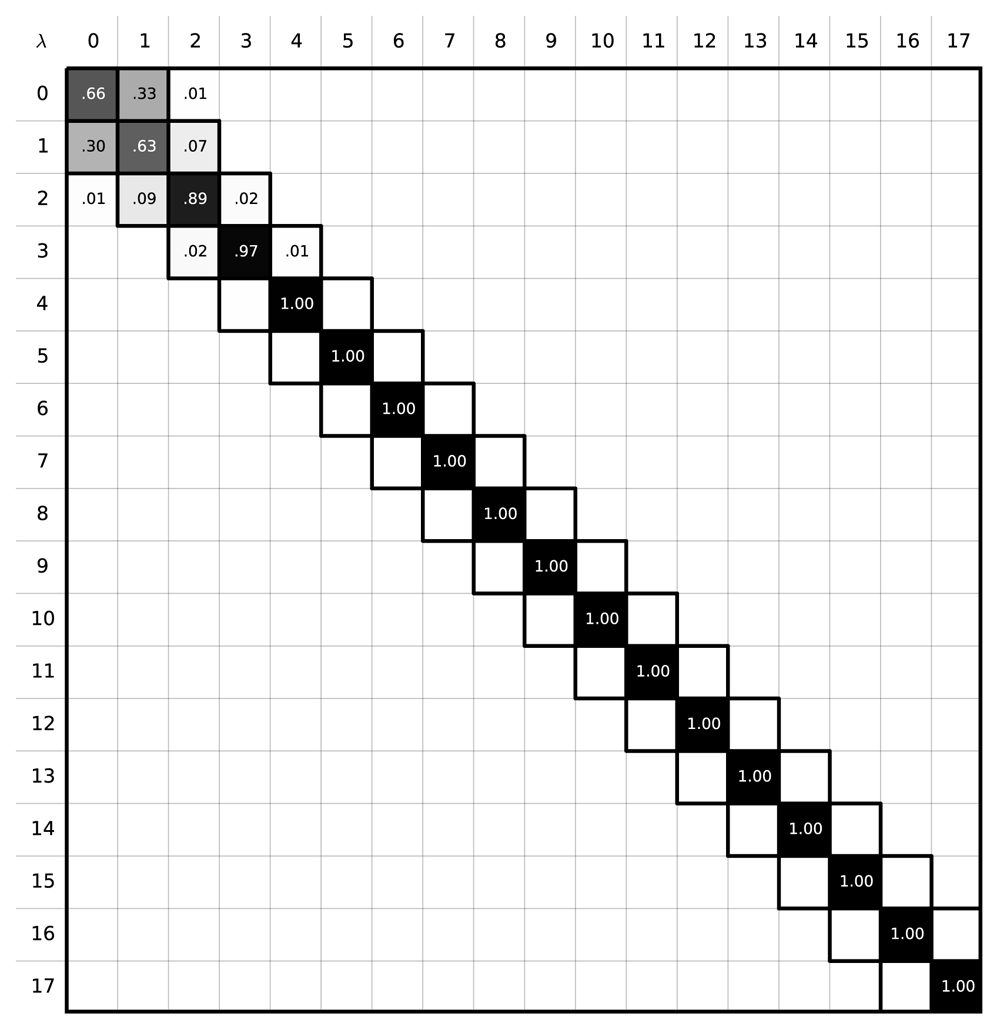
The sum of all the elements in a row should yield 1.0, a probability of 100%. A good free energy estimate is obtained when the states along the alchemical path contain configurations that can be found in other intermediate states. In these situations, the phase space overlap is non-zero, which results in non-zero off-diagonal elements. Here, however, the phase space overlap plot shows that there is no overlap between the states λ_i, 4 ≤ i ≤ 17 indicating poor free energy estimates will result.

Since prior work had appeared to do this estimation successfully⁵², we were uncertain why we were encountering such overlap problems, so we studied an even simpler system. We calculated ∆A_IEM→solid of fcc argon at 4 K with 18 states as in our α-methanol free energy estimation. MBAR yielded an error estimate of infinity, whereas TI estimated ∆A_IEM→solid to be −1666.5(8) k_BT, which, as we show below, is incorrect. This path resulted phase space overlap diagram without overlap between the states after state number 2 (Figure 4). Apparently as the harmonic potential that holds atoms in their lattice positions tends to zero, atoms become rather mobile, dramatically decreasing phase space overlap and leading to poor free energy estimates.

Figure 4. Phase space overlap between the states in the path between IEM and the fcc argon solid.

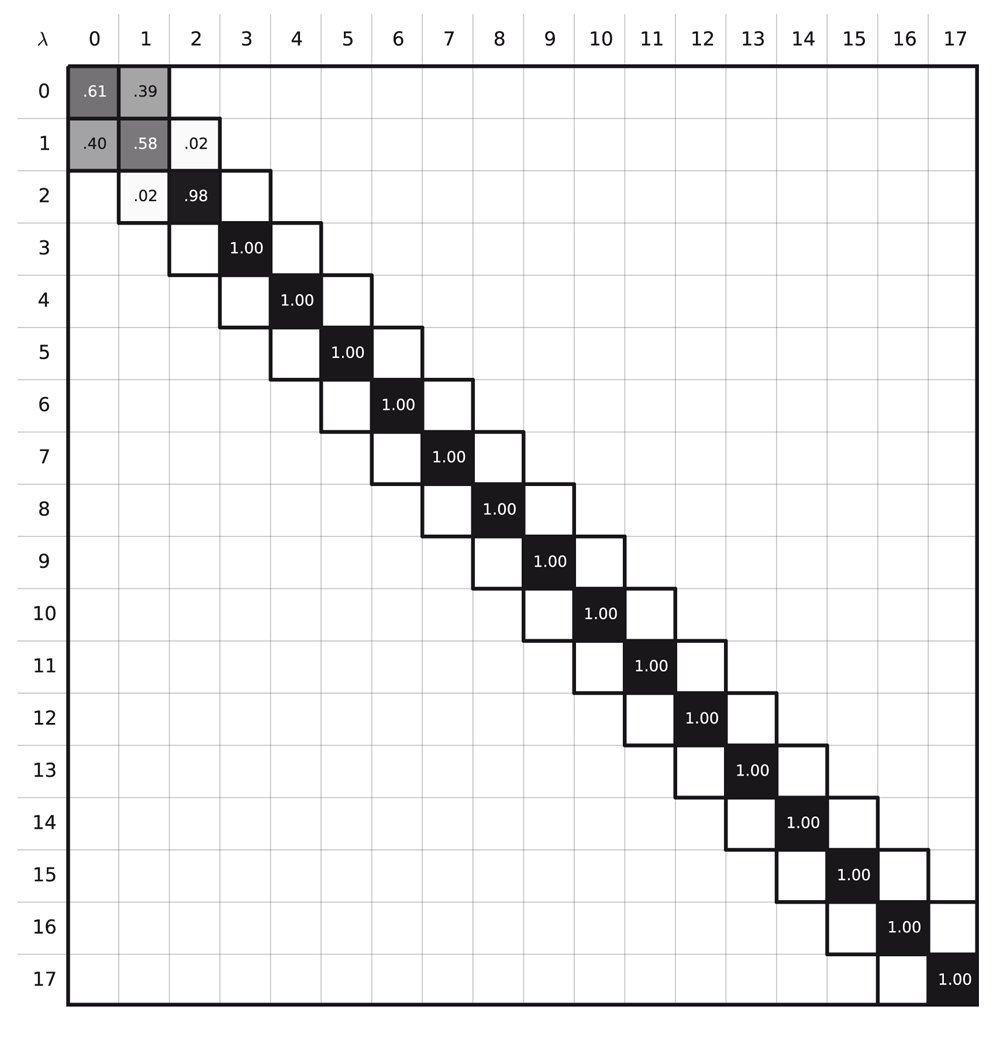
A good free energy estimate is obtained when the states along the alchemical path contain configurations that can be found in other intermediate states. Here, however, the phase space overlap diagram shows that there is no overlap between the states λ_i, 3 ≤ i ≤ 17, which explains the poor quality of the free energy result.

To improve phase space overlap, we introduced more intermediate states along the path for removing the restraints (see Figure 2). We chose to break down the simulation in smaller parts, adding a significant amount of states near the point where the harmonic restraints are approximately zero. The MBAR estimate of ∆A_IEM→solid for fcc argon is −1016.0(2) k_BT using 300 states. TI’s corresponding value was −1017(1) k_BT, differing by far from the (incorrect) value of −1666.5(8) k_BT obtained above with fewer states. Phase space overlap diagrams showed significant improvement in the configuration overlap between the states (Supporting Information). Thus, increasing the number of states was an effective strategy, and we used it in all subsequent calculations.

Even though our α-methanol results were similar to results published previously by other authors⁵², we need to emphasize that reliable free energies resulted from simulations with a large number of intermediate states, as can be seen in Table 1. Despite its conceptual simplicity, calculating the components of the absolute free energy of a solid to a point where there is significant phase space overlap between the intermediate states is computationally demanding. A 900-atom OPLS α-methanol system required 40 states to calculate ∆A_id→IEM, and 600 states for ∆A_IEM→solid.

Table 1. Absolute free energy components for α-methanol at 150 K, in k_BT.

	Literature⁵²	Our replica
A_EM	29.05	29.24
∆A_id→IEM	−41.27(1)	−38.04(7) (EXP) −41.306 56(4) (MBAR, 20 states) −41.275 719(7) (MBAR, 40 states)
∆A_IEM→solid	−17.33(3)	−18.421(5) (TI, 18 states) −18(3) (MBAR, 18 states) −17.1712(6) (TI 600 states) −17.1692(4) (MBAR, 600 states)

We chose these intermediate states in advance, and these ultimately led to free energy errors smaller than 0.1 k_BT; the estimated TI and MBAR values differed by no more than 0.3 k_BT. Our results for ASA using an optimal number of states can be seen in Table 2. The MBAR chemical potential of ASA at 298.15 K equals to −220.67(3) k_BT.

Table 2. Absolute free energy components for polymorph I of acetylsalicylic acid (ASA) at 298.15 K, in k_BT.

	Acetylsalicylic Acid
A_EM	48.047
∆A_id→IEM	−167.316(1) (TI, 118 states) −167.07(3) (MBAR, 118 states)
∆A_IEM→solid	−101.656(2) (TI, 600 states) −101.644(2) (MBAR, 600 states)

The computational cost of calculating A^ASA was high; Each state required a separate simulation (of a 1344-atom ASA system), with 718 states in total. Simulations typically required 11 hours on a single CPU, so the calculation of a single absolute free energy of a molecular solid required approximately 7898 CPU-hours.

Chemical potential of solutions and the solubility of GAFF ASA in TIP3P water

Equation 11 states that the absolute chemical potential of a solution is determined by three quantities: $μ_{i}^{0}$ , the standard chemical potential; $μ_{i}^{e x}$ , the excess chemical potential of the component at a concentration of χ; and a volume-dependent ideal gas component of $k_{B} T \cdot$ ln ( $Λ_{i}^{3} \cdot$ N_ASA/〈V〉_solution). Calculation of $μ_{A S A}^{0}$ only required information regarding the internal structure of the molecule⁵³, thus we estimated $μ_{A S A}^{0}$ by alchemically transforming a single solute molecule into a single Einstein molecule (Table 3), whose absolute free energy we know how to calculate. We used the same number of states that we chose for the solid state simulations and we found that $μ_{A S A}^{0}$ is equal to –150.7(2) k_BT, as discussed in the last subsection of the Methods section.

Table 3. Standard chemical potential of acetylsalicylic acid (ASA) at 298.15 K, in k_BT.

	Acetylsalicylic Acid
$μ_{A S A}^{i d e a l}$	9.3
$μ_{A S A}^{F F o f f}$	65.7409(9) (MBAR 118 states)
$μ_{A S A}^{r e s t r a i n i n g}$	94.3(2) (MBAR 600 states)

Concentrations, volumes and excess chemical potentials can be seen in Table 4. We obtained the excess chemical potentials from solvation free energy calculations^24,28,54. Volumes were obtained from the state in the alchemical path where the solute was fully coupled to the rest of the system.

Table 4. Simulation data for solutions of acetylsalicylic acid in water in different concentrations.

Molar fraction (%)	Volume (nm³)	# solute molecules	# solvent molecules	μ^ex (k_BT)
2.000 e-03	3035.99(5)	2	99998	−16.80(5)
6.666 e-03	911.17(2)	2	30002	−15.88(4)
7.999 e-03	759.33(1)	2	25000	−15.51(5)
9.998 e-03	911.45(3)	3	30003	−15.65(4)
9.999 e-03	607.59(2)	2	20000	−15.47(5)
1.3330 e-02	911.72(2)	4	30004	−15.77(4)
1.3332 e-02	455.84(2)	2	15000	−15.61(4)
1.666 e-02	912.00(3)	5	30005	−15.96(5)
1.9992 e-02	912.27(2)	6	30006	−15.78(4)
1.9996 e-02	304.01(1)	2	10000	−15.62(5)
3.998 e-02	152.25(1)	2	5000	−15.41(6)
1.996 e-01	30.835(7)	2	1000	−16.37(5)
2.991 e-01	31.069(3)	3	1000	−16.40(6)
3.984 e-01	31.309(7)	4	1000	−16.62(6)
4.975 e-01	31.547(3)	5	1000	−17.1(1)

The experimental aqueous solubility of ASA is approximately 0.038% in water at 298 K⁵⁸, but our model predicts that ASA is effectively insoluble in water (Figure 5). While all-atom simulations can yield solubility estimates given adequate simulation time and a correct method, the computed solubility will be that dictated by the underlying energy model or force field, and will not necessarily match experiment. Here, we use GAFF, a general-purpose force field with known limitations^28,71,86,87; apparently, here, the right answer for the force field is not correct. Perhaps this is because of limitations in describing the solid state, as the force field is parameterized for liquid state simulations. Indeed, classical fixed charge force fields have shown severe limitations for polymorph prediction for these reasons^5,31,33–35. Also, point partial atomic charges regularly used in molecular dynamics do not describe electrostatic interactions in a solid particularly well⁸⁸. In the case of the ASA crystal, it is possible that its hydrogen bonds and π-stacking interactions add layers of complexity that are not properly described by GAFF.

Figure 5. Chemical potentials of ASA, solid and solution in different concentrations, with respect to mole fraction.

Discussion

Despite its theoretical rigor, solubility prediction from absolute free energy calculations is a difficult task: it is computationally expensive and, at least in the present approach, requires many different steps and a great deal of care. Here, we attempted to develop and test a general approach to compute the solubility of molecular solids by adapting the EMM to tackle this problem, as discussed above.

To tune our methodology, we initially decided to reproduce the absolute free energy of solid α-methanol, one of methanol’s polymorphs, at 150 K using EMM before doing the same calculations for our compound of choice, ASA. We verified that the free energy differences between the Einstein molecule and the interactive Einstein molecule (∆A_EM→IEM) and between the latter state and the solid (∆A_IEM→solid) were more reliably estimated with the MBAR. The absolute free energy of the crystal (as computed for united-atom OPLS α-methanol) agreed with results found in the literature, which suggested that we were on the right path. We did, however, require a very large number of intermediate alchemical states to obtain accurate free energy estimates, making these simulations fairly computationally demanding

We then chose to calculate the solubility of ASA, owing to its pharmacological importance and its relative complexity compared to previous molecular solids, whose absolute free energies have been computed via EMM previously⁵². As for α-methanol, this calculation required a large number of intermediate alchemical states and considerable computational cost – approximately 8000 CPU hours for a single absolute free energy calculation for the molecular solid, even with the crystal structure as input. Perhaps the number of intermediate states could be further optimized, but clearly a large number of intermediate simulations was required and thus considerable computational cost. Despite all of this, we still could not reproduce the experimental aqueous solubility of ASA; experimentally it is modestly soluble, whereas our work would suggest it is essentially completely insoluble in water, likely due to force field limitations.

The solubility of naphthalene was recently estimated using a similar methodology, the Extended Einstein Crystal Method²³, but with additional approximations. Specifically, since naphthalene molecules interact very weakly with each other in the crystal lattice and with water molecules in solution, the differences between the internal partition function of a naphthalene molecule in the solid and in the solution were assumed to be negligible. This allowed the authors to drop some complexities in treatment of the solution-phase part of the calculation. However, that approach is only suitable for compounds that are only very weakly interacting in solution and in the crystal. ASA, in contrast, is a molecule that interacts strongly with other ASA molecules in its crystal lattice and with water molecules in solution via hydrogen bonds. For instance, an important crystalline feature that is not necessarily present in solution is the dimer structure, with two ASA molecules bound together via hydrogen bonds between the carboxylic acid groups. Differences between the internal partition functions of the molecule in the solid $(q_{A S A}^{s o l i d})$ and in solution $(q_{A S A}^{s o l u t i o n})$ would probably not be negligible in this scenario, thus a more general approach is needed for treatment of such cases. Our work here provides one attempt in that direction.

Overall, the present approach seems to have significant limitations – most notably that the computational expense is considerable, and the resulting estimated solubility is quite inaccurate. Perhaps both of these may be surmountable; GPU-based free energy calculations can be dramatically faster, potentially reducing an 8000 CPU-hour calculation to 80 GPU hours, which would amount to overnight on 8 GPUs, and perhaps this could be optimized via changes to simulation time and number of intermediate states. And with better force fields, perhaps accuracy could be improved; the AMOEBA-based approach of Schnieders shows considerable promise¹⁵. Alternatively, other approaches may be of interest. Solubility has been predicted by simulations using pseudocritical paths (i.e., paths were molecular crystals are transformed in tractable Einstein crystal-like states between the ending states of the transformation^89–92) and a single experimental reference point⁹¹), and with the aid of a thermodynamic cycle formed by the molecular crystal, the molecule in vacuum, and the solvated molecule¹⁵.

We believe the time has come for routine physical methods for estimation of solubility, even if improved force fields prove necessary before results have significant accuracy for application to biomolecular design problems.

Data availability

All data underlying the results are available as part of the article and no additional source data are required.

Competing interests

D.L.M. is a member of the Scientific Advisory Board for OpenEye Scientific Software.

Grant information

D.L.M. and G.D.R.M. appreciate the financial support from the National Science Foundation (CHE 1352608), and computing support from the UCI GreenPlanet cluster, supported in part by NSF Grant CHE-0840513. G.D.R.M. appreciates support from the Brazilian agency CAPES - Science without Borders program (BEX 3932-13-3).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Acknowledgements

The authors would like to thank Dr. Gaetano Calabrò (OpenEye Software), Prof. Michael Shirts (University of Colorado, Boulder), Dr. Eric Dybeck (Pfizer), and Prof. Michael Schnieders (University of Iowa) for fruitful discussions on the project.

Supplementary material

Supporting Information. These files include GROMACS 4.6.7 input parameters for the simulation and all associated MDP files. Also included is a file containing the elements of the phase space overlap matrix of a ∆A_EM→IEM, estimated from an alchemical path of 118 states.

Click here to access the data.

Faculty Opinions recommended

References

1. Pudipeddi M, Serajuddin AT: Trends in solubility of polymorphs. J Pharm Sci. 2005; 94(5): 929–939. PubMed Abstract | Publisher Full Text
2. Bauer J, Spanton S, Henry R, et al.: Ritonavir: an extraordinary example of conformational polymorphism. Pharm Res. 2001; 18(6): 859–866. PubMed Abstract | Publisher Full Text
3. Motherwell WD, Ammon HL, Dunitz JD, et al.: Crystal structure prediction of small organic molecules: A second blind test. Acta Crystallogr B. 2002; 58(Pt 4): 647–661. PubMed Abstract | Publisher Full Text
4. Aaltonen J, Allesø M, Mirza S, et al.: Solid form screening--a review. Eur J Pharm Biopharm. 2009; 71(1): 23–37. PubMed Abstract | Publisher Full Text
5. Bardwell DA, Adjiman CS, Arnautova YA, et al.: Towards crystal structure prediction of complex organic compounds--a report on the fifth blind test. Acta Crystallogr B. 2011; 67(Pt 6): 535–551. PubMed Abstract | Publisher Full Text | Free Full Text
6. Braun DE, McMahon JA, Koztecki LH, et al.: Contrasting Polymorphism of Related Small Molecule Drugs Correlated and Guided by the Computed Crystal Energy Landscape. Cryst Growth Des. 2014; 14(4): 2056–2072. Publisher Full Text
7. Cruz-Cabeza AJ, Bernstein J: Conformational Polymorphism. Chem Rev. 2014; 114(4): 2170–2191. PubMed Abstract | Publisher Full Text
8. Neumann MA, van de Streek J, Fabbiani FP, et al.: Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening. Nat Commun. 2015; 6: 7793. PubMed Abstract | Publisher Full Text | Free Full Text
9. Beran GJ: Modeling Polymorphic Molecular Crystals with Electronic Structure Theory. Chem Rev. 2016; 116(9): 5567–5613. PubMed Abstract | Publisher Full Text
10. Llinàs A, Glen RC, Goodman JM: Solubility Challenge: Can You Predict Solubilities of 32 Molecules Using a Database of 100 Reliable Measurements? J Chem Inf Model. 2008; 48(7): 1289–1303. PubMed Abstract | Publisher Full Text
11. Hopfinger AJ, Esposito EX, Llinàs A, et al.: Findings of the Challenge To Predict Aqueous Solubility. J Chem Inf Model. 2009; 49(1): 1–5. PubMed Abstract | Publisher Full Text
12. Salahinejad M, Le TC, Winkler DA: Aqueous Solubility Prediction: Do Crystal Lattice Interactions Help? Mol Pharm. 2013; 10(7): 2757–2766. PubMed Abstract | Publisher Full Text
13. Palmer DS, Mitchell JB: Is Experimental Data Quality the Limiting Factor in Predicting the Aqueous Solubility of Druglike Molecules? Mol Pharm. 2014; 11(8): 2962–2972. PubMed Abstract | Publisher Full Text
14. Lusci A, Pollastri G, Baldi P: Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules. J Chem Inf Model. 2013; 53(7): 1563–1575. PubMed Abstract | Publisher Full Text | Free Full Text
15. Schnieders MJ, Baltrusaitis J, Shi Y, et al.: The Structure, Thermodynamics and Solubility of Organic Crystals from Simulation with a Polarizable Force Field. J Chem Theory Comput. 2012; 8(5): 1721–1736. PubMed Abstract | Publisher Full Text | Free Full Text
16. Palmer DS, Llinàs A, Morao I, et al.: Predicting Intrinsic Aqueous Solubility by a Thermodynamic Cycle. Mol Pharm. 2008; 5(2): 266–279. PubMed Abstract | Publisher Full Text
17. Westergren J, Lindfors L, Höglund T, et al.: In silico prediction of drug solubility: 1. Free energy of hydration. J Phys Chem B. 2007; 111(7): 1872–1882. PubMed Abstract | Publisher Full Text
18. Lüder K, Lindfors L, Westergren J, et al.: In silico prediction of drug solubility: 2. Free energy of solvation in pure melts. J Phys Chem B. 2007; 111(7): 1883–1892. PubMed Abstract | Publisher Full Text
19. Lüder K, Lindfors L, Westergren J, et al.: In silico prediction of drug solubility. 3. Free energy of solvation in pure amorphous matter. J Phys Chem B. 2007; 111(25): 7303–7311. PubMed Abstract | Publisher Full Text
20. Lüder K, Lindfors L, Westergren J, et al.: In silico prediction of drug solubility: 4. Will simple potentials suffice? J Comput Chem. 2009; 30(12): 1859–1871. PubMed Abstract | Publisher Full Text
21. Ferrario M, Ciccotti G, Spohr E, et al.: Solubility of KF in water by molecular dynamics using the Kirkwood integration method. J Chem Phys. 2002; 117(10): 4947–4953. Publisher Full Text
22. Sanz E, Vega C: Solubility of KF and NaCl in water by molecular simulation. J Chem Phys. 2007; 126(1): 014507. PubMed Abstract | Publisher Full Text
23. Li L, Totton T, Frenkel D: Computational methodology for solubility prediction: Application to the sparingly soluble solutes. J Chem Phys. 2017; 146(21): 214110. PubMed Abstract | Publisher Full Text
24. Klimovich PV, Mobley DL: Predicting hydration free energies using all-atom molecular dynamics simulations and multiple starting conformations. J Comput Aided Mol Des. 2010; 24(4): 307–316. PubMed Abstract | Publisher Full Text
25. Shivakumar D, Williams J, Wu Y, et al.: Prediction of Absolute Solvation Free Energies using Molecular Dynamics Free Energy Perturbation and the OPLS Force Field. J Chem Theory Comput. 2010; 6(5): 1509–1519. PubMed Abstract | Publisher Full Text
26. Shivakumar D, Harder E, Damm W, et al.: Improving the Prediction of Absolute Solvation Free Energies Using the Next Generation OPLS Force Field. J Chem Theory Comput. 2012; 8(8): 2553–2558. PubMed Abstract | Publisher Full Text
27. Skyner RE, McDonagh JL, Groom CR, et al.: A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys Chem Chem Phys. 2015; 17(9): 6174–6191. PubMed Abstract | Publisher Full Text
28. Matos GDR, Kyu DY, Loeffler HH, et al.: Approaches for calculating solvation free energies and enthalpies demonstrated with an update of the FreeSolv database. J Chem Eng Data. 2017; 62(5): 1559–1569. PubMed Abstract | Publisher Full Text | Free Full Text
29. Boulanger E, Huang L, Rupakheti C, et al.: Optimized Lennard-Jones Parameters for Druglike Small Molecules. J Chem Theory Comput. 2018. PubMed Abstract | Publisher Full Text
30. Price SL: The computational prediction of pharmaceutical crystal structures and polymorphism. Adv Drug Deliv Rev. 2004; 56(3): 301–319. PubMed Abstract | Publisher Full Text
31. Day GM, Motherwell WD, Ammon HL, et al.: A third blind test of crystal structure prediction. Acta Crystallogr B. 2005; 61(Pt 5): 511–527. PubMed Abstract | Publisher Full Text
32. Woodley SM, Catlow R: Crystal structure prediction from first principles. Nat Mater. 2008; 7(12): 937–46. PubMed Abstract | Publisher Full Text
33. Day GM, Cooper TG, Cruz-Cabeza AJ, et al.: Significant progress in predicting the crystal structures of small organic molecules--a report on the fourth blind test. Acta Crystallogr B. 2009; 65(Pt 2): 107–125. PubMed Abstract | Publisher Full Text
34. Price SS: Computed crystal energy landscapes for understanding and predicting organic crystal structures and polymorphism. Acc Chem Res. 2009; 42(1): 117–126. PubMed Abstract | Publisher Full Text
35. Reilly AM, Cooper RI, Adjiman CS, et al.: Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr B Struct Sci Cryst Eng Mater. 2016; 72(Pt 4): 439–459. PubMed Abstract | Publisher Full Text | Free Full Text
36. Chipot C, Pohorille A: Free Energy Calculations Theory and Applications in Chemistry and Biology. Springer, 2007. Publisher Full Text
37. Chipot C: Frontiers in free-energy calculations of biological systems. WIREs Comput Mol Sci. 2014; 4(1): 71–89. Publisher Full Text
38. Shirts MR, Mobley DL, Chodera JD: Alchemical Free Energy Calculations: Ready for Prime Time? In DC. Spellmeyer and R. Wheeler, editors, Annu Rep Comput Chem. Elsevier. 2007; 3: 41–59. Publisher Full Text
39. Kirkwood JG: Statistical Mechanics of Fluid Mixtures. J Chem Phys. 1935; 3(5): 300–313. Publisher Full Text
40. Ytreberg FM, Swendsen RH, Zuckerman DM: Comparison of free energy methods for molecular systems. J Chem Phys. 2006; 125(18): 184114. PubMed Abstract | Publisher Full Text
41. Shirts MR, Pande VS: Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J Chem Phys. 2005; 122(14): 144107. PubMed Abstract | Publisher Full Text
42. Paliwal H, Shirts MR: A Benchmark Test Set for Alchemical Free Energy Transformations and Its Use to Quantify Error in Common Free Energy Methods. J Chem Theory Comput. 2011; 7(12): 4115–4134. PubMed Abstract | Publisher Full Text
43. Zwanzig RW: High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J Chem Phys. 1954; 22(8): 1420–1426. Publisher Full Text
44. Bennett CH: Efficient estimation of free energy differences from Monte Carlo data. J Comp Phys. 1976; 22(2): 245–268. Publisher Full Text
45. Wu D, Kofke DA: Asymmetric bias in free-energy perturbation measurements using two Hamiltonian-based models. Phys Rev E Stat Nonlin Soft Matter Phys. 2004; 70(6 Pt 2): 066702. PubMed Abstract | Publisher Full Text
46. Wu D, Kofke DA: Phase-space overlap measures. I. Fail-safe bias detection in free energies calculated by molecular simulation. J Chem Phys. 2005; 123(5): 54103. PubMed Abstract | Publisher Full Text
47. Frenkel D, Ladd AJC: New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres. J Chem Phys. 1984; 81(7): 3188–3193. Publisher Full Text
48. Vega C, Sanz E, Abascal JLF, et al.: Determination of phase diagrams via computer simulation: Methodology and applications to water, electrolytes and proteins. J Phys Condens Matter. 2008; 20(15): 153101. Publisher Full Text
49. Noya EG, Conde MM, Vega C: Computing the free energy of molecular solids by the Einstein molecule approach: ices XIII and XIV, hard-dumbbells and a patchy model of proteins. J Chem Phys. 2008; 129(10): 104704. PubMed Abstract | Publisher Full Text
50. Vega C, Noya EG: Revisiting the Frenkel-Ladd method to compute the free energy of solids: the Einstein molecule approach. J Chem Phys. 2007; 127(15): 154113. PubMed Abstract | Publisher Full Text
51. Aragones JL, Sanz E, Vega C: Solubility of NaCl in water by molecular simulation revisited. J Chem Phys. 2012; 136(24): 244508. PubMed Abstract | Publisher Full Text
52. Aragones JL, Noya EG, Valeriani C, et al.: Free energy calculations for molecular solids using GROMACS. J Chem Phys. 2013; 139(3): 034104. PubMed Abstract | Publisher Full Text
53. Ben-Naim A: Molecular Theory of Solutions. Oxford University Press, Oxford, 2006. Reference Source
54. Mobley DL, Guthrie JP: FreeSolv: a database of experimental and calculated hydration free energies, with input files. J Comput Aided Mol Des. 2014; 28(7): 711–720. PubMed Abstract | Publisher Full Text | Free Full Text
55. Benavides AL, Aragones JL, Vega C: Consensus on the solubility of NaCl in water from computer simulations using the chemical potential route. J Chem Phys. 2016; 144(12): 124504. PubMed Abstract | Publisher Full Text
56. Park J, Nessler I, McClain B, et al.: Absolute Organic Crystal Thermodynamics: Growth of the Asymmetric Unit into a Crystal via Alchemy. J Chem Theory Comput. 2014; 10(7): 2781–2791. PubMed Abstract | Publisher Full Text
57. Kim Y, Machida K, Taga T, et al.: Structure redetermination and packing analysis of aspirin crystal. Chem Pharm Bull (Tokyo). 1985; 33(7): 2641–2647. PubMed Abstract | Publisher Full Text
58. Yalkowsky SH, He Y, Jain P: Handbook of Aqueous Solubility Data. CRC Press, second edition, 2010. Reference Source
59. Henshaw DG: Atomic Distribution in Liquid and Solid Neon and Solid Argon by Neutron Diffraction. Phys Rev. 1958; 111(6): 1470–1475. Publisher Full Text
60. Berendsen HJC, van der Spoel D, van Drunen R: GROMACS: A message-passing parallel molecular dynamics implementation. Comput Phys Comm. 1995; 91(1): 43–56. Publisher Full Text
61. Van Der Spoel D, Lindahl E, Hess B, et al.: GROMACS: fast, flexible, and free. J Comput Chem. 2005; 26(16): 1701–1718. PubMed Abstract | Publisher Full Text
62. Hess B, Kutzner C, van der Spoel D, et al.: GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J Chem Theory Comput. 2008; 4(3): 435–447. PubMed Abstract | Publisher Full Text
63. Pronk S, Páll S, Schulz R, et al.: GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013; 29(7): 845–854. PubMed Abstract | Publisher Full Text | Free Full Text
64. Jakalian A, Bush BL, Jack DB, et al.: Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J Comput Chem. 2000; 21(2): 132–146. Publisher Full Text
65. Jakalian A, Jack DB, Bayly CI: Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J Comput Chem. 2002; 23(16): 1623–1641. PubMed Abstract | Publisher Full Text
66. Parrinello M, Rahman A: Polymorphic transitions in single crystals: A new molecular dynamics method. J Appl Phys. 1981; 52(12): 7182. Publisher Full Text
67. Jorgensen WL, Chandrasekhar J, Madura JD, et al.: Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983; 79(2): 926–935. Publisher Full Text
68. Macrae CF, Edgington PR, McCabe P, et al.: Mercury: Visualization and analysis of crystal structures. J Appl Cryst. 2006; 39(3): 453–457. Publisher Full Text
69. Case DA, Cheatham TE 3rd, Darden T, et al.: The Amber biomolecular simulation programs. J Comput Chem. 2005; 26(16): 1668–1688. PubMed Abstract | Publisher Full Text | Free Full Text
70. Salomon-Ferrer R, Case DA, Walker RC: An overview of the Amber biomolecular simulation package. WIREs Comput Mol Sci. 2013; 3(2): 198–210. Publisher Full Text
71. Cheatham TE 3rd, Case DA: Twenty-five years of nucleic acid simulations. Biopolymers. 2013; 99(12): 969–977. PubMed Abstract | Publisher Full Text | Free Full Text
72. Case DA, Babin V, Berryman JT, et al.: Amber 14. 2014. Reference Source
73. Swails J, Hernandez C, Mobley DL, et al.: Parmed. (accessed October 9, 2015).
74. Shirts MR, Chodera JD: Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys. 2008; 129(12): 124105. PubMed Abstract | Publisher Full Text | Free Full Text
75. Klimovich PV, Mobley DL: A Python tool to set up relative free energy calculations in GROMACS. J Comput Aided Mol Des. 2015; 29(11): 1007–1014. PubMed Abstract | Publisher Full Text | Free Full Text
76. de Ruiter A, Boresch S, Oostenbrink C: Comparison of thermodynamic integration and Bennett acceptance ratio for calculating relative protein-ligand binding free energies. J Comp Chem. 2013; 34(12): 1024–1034. PubMed Abstract | Publisher Full Text
77. Bannan CC, Calabró G, Kyu DY, et al.: Calculating Partition Coefficients of Small Molecules in Octanol/Water and Cyclohexane/Water. J Chem Theory Comp. 2016; 12(8): 4015–4024. PubMed Abstract | Publisher Full Text | Free Full Text
78. Martínez L, Andrade R, Birgin EG, et al.: PACKMOL: a package for building initial configurations for molecular dynamics simulations. J Comp Chem. 2009; 30(13): 2157–2164. PubMed Abstract | Publisher Full Text
79. Beauchamp KA, Rustenburg AS, Rizzi A, et al.: OpenMolTools.
80. Inc: OpeneEye Scientific Software. OEChem Toolkit, 2010; (accessed June 16, 2015).
81. Inc: OpeneEye Scientific Software. QUACPAC 1.7.0.2.
82. Hawkins PC, Nicholls A: Conformer generation with OMEGA: learning from the data set and the analysis of failures. J Chem Inf Model. 2012; 52(11): 2919–2936. PubMed Abstract | Publisher Full Text
83. Frenkel D, Smit B: Understanding Molecular Simulation: From Algorithms to Applications. Academic Press Inc. (London) Ltd., 1996; 1. Reference Source
84. Pohorille A, Jarzynski C, Chipot C: Good Practices in Free-Energy Calculations. J Phys Chem B. 2010; 114(32): 10235–10253. PubMed Abstract | Publisher Full Text
85. Klimovich PV, Shirts MR, Mobley DL: Guidelines for the analysis of free energy calculations. J Comput Aided Mol Des. 2015; 29(5): 397–411. PubMed Abstract | Publisher Full Text | Free Full Text
86. Mobley DL, Dumont E, Chodera JD, et al.: Comparison of charge models for fixed-charge force fields: small-molecule hydration free energies in explicit solvent. J Phys Chem B. 2007; 111(9): 2242–2254. PubMed Abstract | Publisher Full Text
87. Fennell CJ, Wymer KL, Mobley DL: A fixed-charge model for alcohol polarization in the condensed phase, and its role in small molecule hydration. J Phys Chem B. 2014; 118(24): 6438–6446. PubMed Abstract | Publisher Full Text | Free Full Text
88. Kramer C, Spinn A, Liedl KR: Charge Anisotropy: Where Atomic Multipoles Matter Most. J Chem Theory Comput. 2014; 10(10): 4488–4496. PubMed Abstract | Publisher Full Text
89. Eike DM, Brennecke JF, Maginn EJ: Toward a robust and general molecular simulation method for computing solid-liquid coexistence. J Chem Phys. 2005; 122(1): 14115. PubMed Abstract | Publisher Full Text
90. Eike DM, Maginn EJ: Atomistic simulation of solid-liquid coexistence for molecular systems: application to triazole and benzene. J Chem Phys. 2006; 124(16): 164503. PubMed Abstract | Publisher Full Text
91. Paluch AS, Jayaraman S, Shah JK, et al.: A method for computing the solubility limit of solids: application to sodium chloride in water and alcohols. J Chem Phys. 2010; 133(12): 124504. PubMed Abstract | Publisher Full Text
92. Dybeck EC, Schieber NP, Shirts MR: Effects of a More Accurate Polarizable Hamiltonian on Polymorph Free Energies Computed Efficiently by Reweighting Point-Charge Potentials. J Chem Theory Comput. 2016; 12(8): 3491–3505. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 31 May 2018

Author details Author details

Guilherme Duarte Ramos Matos
Roles: Conceptualization, Data Curation, Investigation, Methodology, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

David L. Mobley
Roles: Conceptualization, Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Writing – Review & Editing

Competing interests

D.L.M. is a member of the Scientific Advisory Board for OpenEye Scientific Software.

Grant information

Article Versions (2)

version 2

Revised

Published: 04 Jan 2019, 7:686

https://doi.org/10.12688/f1000research.14960.2

version 1

Published: 31 May 2018, 7:686

https://doi.org/10.12688/f1000research.14960.1

© 2018 Duarte Ramos Matos G and Mobley DL. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Duarte Ramos Matos G and Mobley DL. Challenges in the use of atomistic simulations to predict solubilities of drug-like molecules [version 1; peer review: 2 approved]. F1000Research 2018, 7:686 (https://doi.org/10.12688/f1000research.14960.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 31 May 2018

Views

Reviewer Report 25 Jul 2018

Eric C. Dybeck, Pfizer, Groton, CT, USA

Approved

https://doi.org/10.5256/f1000research.16287.r36225

Summary and Overall Impressions
This article seeks to explore the application (and challenges) of using atomistic simulations to compute the solubility of drug-like small molecules. The ability to predict the solubility of emerging drug candidates is indeed an important challenge for the pharmaceutical industry, as many drugs which come out of discovery are BCS class II or IV with low aqueous solubility. The method proposed in this work could in principle allow medicinal chemists and pharmaceutical scientists to evaluate drug solubility early in the development pipeline and accelerate product release. This method is sufficiently novel and well executed to deserve publication in this scientific journal. The authors have also done a fantastic job including the details and input files necessary for one well-versed in the art to reproduce their results. Minor revisions are suggested below to further improve the clarity and quality of the article.

Suggested Revisions

In the original papers by Aragones, Noya, and Vega, the molecules were constrained to be completely rigid. In this work, the investigators appear use this method for both constrained and fully flexible molecular systems. The authors should consider highlighting this expanded capability, and perhaps discuss the tradeoffs in accuracy and simulation speed between flexible vs rigid molecular treatment for absolute solubility prediction.
The authors use both the term ‘restraints’ and ‘constraints’ to describe the harmonic potential being applied and removed from atoms in the system. It may be more clear to consistently refer to these alchemical harmonic potentials as ‘restraints’ and reserve the term ‘constraint’ for the subroutine used to keep molecules fully rigid.
An important feature in the Einstein molecule method utilized herein is the use of a frozen reference atom rather than the traditional full-system center-of-mass removal. In principle, the free energy to add restraints to a system with a frozen atom will be independent of the choice of reference. In practice, some choices of reference atom may lead to faster simulation convergence than others due to differences in the fluctuation magnitude of the atoms around their natural lattice positions. It would be useful to discuss best practices in how one chose the frozen reference atom, as well as to discuss the effect of different reference choices on the convergence of the various alchemical steps in this workflow.
The authors mention using a previously developed Monte Carlo code to compute the absolute free energy of the reference Einstein Molecule state. It would be useful to comment on the uncertainty inherent in this component of the overall free energy calculation. For example, how much variance would ten independent calls to the Monte Carlo program have for these compounds?
On page 7 of the paper, the authors briefly mention that “GROMACS only reads each lambda value up to the 4^th decimal place”. In my own alchemical simulations with GROMACS, I have routinely used lambda values out to 8 decimal places. If this is a version-specific limitation, the authors should state this explicitly. Otherwise, this comment should be removed.
The investigators chose to use linear spacing for the lambda values in all alchemical processes including the addition of harmonic restraints to the physical system. They also note that adding harmonic restraints represented the most time-intensive part of the overall workflow and required splitting into 6 different steps of increasing restraint strength. Furthermore, they find that the overlap between neighboring lambda states during the restraint addition is quite low (Figure 2-4) and produces large uncertainties in their final free energy estimates. In my own investigations of adding harmonic restraints to solids from 2016 (cited in this work) I observed that either cubically- or quartically- spaced lambda values significantly improve the overlap along the thermodynamic path relative to linear spacing and reduce the total amount of simulation cost. This should be included as a potential remedy for the high simulation cost lamented in the discussion section of the paper.
The investigators chose to use a large value of >1,000,000 kJ/nm/mol for their final restraint state to add or remove inter-particle interactions. It is necessary to have strong restraints in order to remove stiff degrees of freedom such as bonds and angles. However, it is possible that the interaction removal could be achieved with a weaker value of the restraint constant, and this would in turn reduce the number of simulations to add or remove harmonic restraints. This should also be discussed in the context of ways to reduce the amount of simulation expense observed for these calculations.
Finally, the authors should consider including the additional papers of Sellers et al. 2016¹ and Schilling and Schmid 2009² who also explore the use of atomistic simulation to compute absolute solid free energies. These articles also discuss how to apply restraints in a manner that preserves the indistinguishability of certain particles. It would be worth discussing ways to account for particle indistinguishablility in the method presented in this paper.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

1. Sellers MS, Lísal M, Brennan JK: Free-energy calculations using classical molecular simulation: application to the determination of the melting point and chemical potential of a flexible RDX model.Phys Chem Chem Phys. 2016; 18 (11): 7841-50 PubMed Abstract | Publisher Full Text
2. Schilling T, Schmid F: Computing absolute free energies of disordered structures by molecular simulation.J Chem Phys. 2009; 131 (23): 231102 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Reader Comment 04 Jan 2019

David Mobley

04 Jan 2019

Reader Comment

We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your ... Continue reading We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your point 1:

We appreciate the your point that our use of this for “flexible” molecules (even if not particularly flexible) is potentially an extension of earlier work and have amended our manuscript accordingly. We also added a couple of sentences highlighting that this works on molecules which are somewhat flexible, though pointing out that the molecules here are not especially floppy and the method may not work as well on especially floppy molecules.

It's worth noting that our molecules are not as flexible as the word might imply. Acetylsalicylic acid is made of an aromatic ring bonded to a carboxyl group and an acetyl group in the ortho position. In the crystal structure the ring and the carboxyl group are rather rigid in the same plane -- there are hydrogen bonds between two ASA molecules forming a dimer -- and the only flexible part of the molecule is the acetyl group. EMM would probably not perform well if the crystal contained very floppy carbon chains -- butyl, pentyl, hexyl, and so on. On this case, since the “core” of the molecule is reasonably rigid and the acetyl group on the side rather fixed in a position due to the spacial arrangement.

To your point 3, as we discussed by e-mail, in this study, we chose the frozen reference in arbitrary manner. In principle the choice of reference atom does not matter. For acetylsalicylic acid we selected one of the carbon atoms in the aromatic ring. It is not uncommon in free energy calculations of various types, including binding free energy calculations, to have to make arbitrary choices in which atoms to restrain or other considerations, and several studies have demonstrated that such choices in practice are unimportant, so applying a similar approach here was not a cause for concern. We have not examined this issue carefully. The revision now addresses this.

To your point 4, the integrator is not very robust. It requires a lot of parameter-tweaking, as it was outlined in Aragonès et al. For methanol, the uncertainty is +- 0.09. For ASA, the uncertainty is +- 3 kT (an orientation change parameters need to be optimized for each case). We added a couple of sentences discussing this to the paper. Presumably this could be a point for future optimization.

We addressed all your other points by making changes/additions to the text, including a rather extensive new discussion for potential places for optimization.
We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your point 1:

We appreciate the your point that our use of this for “flexible” molecules (even if not particularly flexible) is potentially an extension of earlier work and have amended our manuscript accordingly. We also added a couple of sentences highlighting that this works on molecules which are somewhat flexible, though pointing out that the molecules here are not especially floppy and the method may not work as well on especially floppy molecules.

It's worth noting that our molecules are not as flexible as the word might imply. Acetylsalicylic acid is made of an aromatic ring bonded to a carboxyl group and an acetyl group in the ortho position. In the crystal structure the ring and the carboxyl group are rather rigid in the same plane -- there are hydrogen bonds between two ASA molecules forming a dimer -- and the only flexible part of the molecule is the acetyl group. EMM would probably not perform well if the crystal contained very floppy carbon chains -- butyl, pentyl, hexyl, and so on. On this case, since the “core” of the molecule is reasonably rigid and the acetyl group on the side rather fixed in a position due to the spacial arrangement.

To your point 3, as we discussed by e-mail, in this study, we chose the frozen reference in arbitrary manner. In principle the choice of reference atom does not matter. For acetylsalicylic acid we selected one of the carbon atoms in the aromatic ring. It is not uncommon in free energy calculations of various types, including binding free energy calculations, to have to make arbitrary choices in which atoms to restrain or other considerations, and several studies have demonstrated that such choices in practice are unimportant, so applying a similar approach here was not a cause for concern. We have not examined this issue carefully. The revision now addresses this.

To your point 4, the integrator is not very robust. It requires a lot of parameter-tweaking, as it was outlined in Aragonès et al. For methanol, the uncertainty is +- 0.09. For ASA, the uncertainty is +- 3 kT (an orientation change parameters need to be optimized for each case). We added a couple of sentences discussing this to the paper. Presumably this could be a point for future optimization.

We addressed all your other points by making changes/additions to the text, including a rather extensive new discussion for potential places for optimization.
Competing Interests: None. The review was excellent. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Reader Comment 04 Jan 2019

David Mobley

04 Jan 2019

Reader Comment

We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your ... Continue reading We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your point 1:

We appreciate the your point that our use of this for “flexible” molecules (even if not particularly flexible) is potentially an extension of earlier work and have amended our manuscript accordingly. We also added a couple of sentences highlighting that this works on molecules which are somewhat flexible, though pointing out that the molecules here are not especially floppy and the method may not work as well on especially floppy molecules.

It's worth noting that our molecules are not as flexible as the word might imply. Acetylsalicylic acid is made of an aromatic ring bonded to a carboxyl group and an acetyl group in the ortho position. In the crystal structure the ring and the carboxyl group are rather rigid in the same plane -- there are hydrogen bonds between two ASA molecules forming a dimer -- and the only flexible part of the molecule is the acetyl group. EMM would probably not perform well if the crystal contained very floppy carbon chains -- butyl, pentyl, hexyl, and so on. On this case, since the “core” of the molecule is reasonably rigid and the acetyl group on the side rather fixed in a position due to the spacial arrangement.

To your point 3, as we discussed by e-mail, in this study, we chose the frozen reference in arbitrary manner. In principle the choice of reference atom does not matter. For acetylsalicylic acid we selected one of the carbon atoms in the aromatic ring. It is not uncommon in free energy calculations of various types, including binding free energy calculations, to have to make arbitrary choices in which atoms to restrain or other considerations, and several studies have demonstrated that such choices in practice are unimportant, so applying a similar approach here was not a cause for concern. We have not examined this issue carefully. The revision now addresses this.

To your point 4, the integrator is not very robust. It requires a lot of parameter-tweaking, as it was outlined in Aragonès et al. For methanol, the uncertainty is +- 0.09. For ASA, the uncertainty is +- 3 kT (an orientation change parameters need to be optimized for each case). We added a couple of sentences discussing this to the paper. Presumably this could be a point for future optimization.

We addressed all your other points by making changes/additions to the text, including a rather extensive new discussion for potential places for optimization.
We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your point 1:

We appreciate the your point that our use of this for “flexible” molecules (even if not particularly flexible) is potentially an extension of earlier work and have amended our manuscript accordingly. We also added a couple of sentences highlighting that this works on molecules which are somewhat flexible, though pointing out that the molecules here are not especially floppy and the method may not work as well on especially floppy molecules.

It's worth noting that our molecules are not as flexible as the word might imply. Acetylsalicylic acid is made of an aromatic ring bonded to a carboxyl group and an acetyl group in the ortho position. In the crystal structure the ring and the carboxyl group are rather rigid in the same plane -- there are hydrogen bonds between two ASA molecules forming a dimer -- and the only flexible part of the molecule is the acetyl group. EMM would probably not perform well if the crystal contained very floppy carbon chains -- butyl, pentyl, hexyl, and so on. On this case, since the “core” of the molecule is reasonably rigid and the acetyl group on the side rather fixed in a position due to the spacial arrangement.

To your point 3, as we discussed by e-mail, in this study, we chose the frozen reference in arbitrary manner. In principle the choice of reference atom does not matter. For acetylsalicylic acid we selected one of the carbon atoms in the aromatic ring. It is not uncommon in free energy calculations of various types, including binding free energy calculations, to have to make arbitrary choices in which atoms to restrain or other considerations, and several studies have demonstrated that such choices in practice are unimportant, so applying a similar approach here was not a cause for concern. We have not examined this issue carefully. The revision now addresses this.

To your point 4, the integrator is not very robust. It requires a lot of parameter-tweaking, as it was outlined in Aragonès et al. For methanol, the uncertainty is +- 0.09. For ASA, the uncertainty is +- 3 kT (an orientation change parameters need to be optimized for each case). We added a couple of sentences discussing this to the paper. Presumably this could be a point for future optimization.

We addressed all your other points by making changes/additions to the text, including a rather extensive new discussion for potential places for optimization.
Competing Interests: None. The review was excellent. Close
Report a concern

Views

Reviewer Report 25 Jun 2018

Lillian T. Chong, Department of Chemistry, University of Pittsburgh, Pittsburgh, PA, USA

Anthony T. Bogetti, Department of Chemistry, University of Pittsburgh, Pittsburgh, PA, USA

Approved

https://doi.org/10.5256/f1000research.16287.r34597

The authors report extensive computations of absolute chemical potentials to predict the solubility of the drug, acetylsalicylic acid (aspirin), using molecular dynamics simulations. The manuscript is clearly written, providing the relevant background for understanding their results, a non-trivial task for this subject matter. A non-expert in the field of statistical mechanics should have little trouble reading this paper due to such careful and effective writing. In addition, figures such as Figure 1 are well constructed and greatly aid in the understanding of the relevant theory. While the results are not ideal, the challenges and limitations that have been revealed are informative and important for moving forward in the field of drug discovery. This manuscript would be of broad interest to life scientists. I recommend indexing of this manuscript in F1000Research.

I have only a few comments for minor revisions:

Introduction section: This section could be re-framed to accentuate the positive, informative aspects of this manuscript’s results. For instance, it would be worth mentioning the fact that the new thermodynamic cycle employed in this study was able to enhance solubility calculations of the methanol system, an important feature of this manuscript that should be highlighted early on. In addition, the example of Norvir in the first paragraph could be shortened considerably, and similar shortening of the Introduction could be more effective in presenting the broader impacts of this study.
Theory section: This section would benefit from a clear definition of an Einstein crystal for life scientists at the very beginning. Also important would be to include early in the Theory section explanations of the ECM and EMM cycles and logically structuring the rest of the section from there, including more fundamental equations as needed. Also, it is not clear in equation (5) what is meant by averaging over the configurations of the initial state. Please clarify.
Distinctives of this Work section: It would be beneficial to remind the reader of the unique aspects of the EMM method over ECM since the implementation of this method is the novel in the manuscript.
Methods section, third paragraph: It was not clear to this reader which temperatures were used for the liquid simulations. Please clearly mention the temperatures. If the simulations were run at 4 K, then the authors should comment on the accuracy of the TIP3P water model at this very low temperature.
Discussion section, second to last paragraph: The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Reader Comment 28 Jun 2018

David Mobley

28 Jun 2018

Reader Comment

Thanks, Lillian! This is extremely helpful; we'll work to address these issues.
(This is our first time experimenting with this platform and so far it's a huge success; I like ... Continue reading Thanks, Lillian! This is extremely helpful; we'll work to address these issues.
(This is our first time experimenting with this platform and so far it's a huge success; I like having the feedback attached publicly to the actual article. Now I just have to figure out how revising works...)
Thanks, Lillian! This is extremely helpful; we'll work to address these issues.
(This is our first time experimenting with this platform and so far it's a huge success; I like having the feedback attached publicly to the actual article. Now I just have to figure out how revising works...)
Competing Interests: No competing interests were disclosed. Close
Report a concern
Reader Comment 28 Jun 2018

David Mobley

28 Jun 2018

Reader Comment

I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two ... Continue reading I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

I agree that other force fields might be worth trying before switching to polarizable approaches. However, ff15ipq and ff15fb are protein/nucleic acid force fields and don't cover general small molecules. We ARE working on better general small molecule force fields, though, and hopefully some day we can try those.
I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

I agree that other force fields might be worth trying before switching to polarizable approaches. However, ff15ipq and ff15fb are protein/nucleic acid force fields and don't cover general small molecules. We ARE working on better general small molecule force fields, though, and hopefully some day we can try those.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Reader Comment 04 Jan 2019

David Mobley

04 Jan 2019

Reader Comment

We just submitted a revised version with changes along these lines. Thanks again for your feedback.
Competing Interests: No competing interests were disclosed.
We just submitted a revised version with changes along these lines. Thanks again for your feedback.
We just submitted a revised version with changes along these lines. Thanks again for your feedback.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Reader Comment 28 Jun 2018

David Mobley

28 Jun 2018

Reader Comment

Thanks, Lillian! This is extremely helpful; we'll work to address these issues.
(This is our first time experimenting with this platform and so far it's a huge success; I like ... Continue reading Thanks, Lillian! This is extremely helpful; we'll work to address these issues.
(This is our first time experimenting with this platform and so far it's a huge success; I like having the feedback attached publicly to the actual article. Now I just have to figure out how revising works...)
Thanks, Lillian! This is extremely helpful; we'll work to address these issues.
(This is our first time experimenting with this platform and so far it's a huge success; I like having the feedback attached publicly to the actual article. Now I just have to figure out how revising works...)
Competing Interests: No competing interests were disclosed. Close
Report a concern
Reader Comment 28 Jun 2018

David Mobley

28 Jun 2018

Reader Comment

I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two ... Continue reading I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

I agree that other force fields might be worth trying before switching to polarizable approaches. However, ff15ipq and ff15fb are protein/nucleic acid force fields and don't cover general small molecules. We ARE working on better general small molecule force fields, though, and hopefully some day we can try those.
I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

I agree that other force fields might be worth trying before switching to polarizable approaches. However, ff15ipq and ff15fb are protein/nucleic acid force fields and don't cover general small molecules. We ARE working on better general small molecule force fields, though, and hopefully some day we can try those.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Reader Comment 04 Jan 2019

David Mobley

04 Jan 2019

Reader Comment

We just submitted a revised version with changes along these lines. Thanks again for your feedback.
Competing Interests: No competing interests were disclosed.
We just submitted a revised version with changes along these lines. Thanks again for your feedback.
We just submitted a revised version with changes along these lines. Thanks again for your feedback.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 31 May 2018

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 04 Jan 19
Version 1 31 May 18	read	read

Lillian T. Chong, University of Pittsburgh, Pittsburgh, USA

Anthony T. Bogetti, University of Pittsburgh, Pittsburgh, USA
Eric C. Dybeck, Pfizer, Groton, USA

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

22 Views

25 Jul 2018 | for Version 1

Eric C. Dybeck, Pfizer, Groton, CT, USA

22 Views Cite this report Responses(1)

Approved

In the original papers by Aragones, Noya, and Vega, the molecules were constrained to be completely rigid. In this work, the investigators appear use this method for both constrained and fully flexible molecular systems. The authors should consider highlighting this expanded capability, and perhaps discuss the tradeoffs in accuracy and simulation speed between flexible vs rigid molecular treatment for absolute solubility prediction.
The authors use both the term ‘restraints’ and ‘constraints’ to describe the harmonic potential being applied and removed from atoms in the system. It may be more clear to consistently refer to these alchemical harmonic potentials as ‘restraints’ and reserve the term ‘constraint’ for the subroutine used to keep molecules fully rigid.
An important feature in the Einstein molecule method utilized herein is the use of a frozen reference atom rather than the traditional full-system center-of-mass removal. In principle, the free energy to add restraints to a system with a frozen atom will be independent of the choice of reference. In practice, some choices of reference atom may lead to faster simulation convergence than others due to differences in the fluctuation magnitude of the atoms around their natural lattice positions. It would be useful to discuss best practices in how one chose the frozen reference atom, as well as to discuss the effect of different reference choices on the convergence of the various alchemical steps in this workflow.
The authors mention using a previously developed Monte Carlo code to compute the absolute free energy of the reference Einstein Molecule state. It would be useful to comment on the uncertainty inherent in this component of the overall free energy calculation. For example, how much variance would ten independent calls to the Monte Carlo program have for these compounds?
On page 7 of the paper, the authors briefly mention that “GROMACS only reads each lambda value up to the 4^th decimal place”. In my own alchemical simulations with GROMACS, I have routinely used lambda values out to 8 decimal places. If this is a version-specific limitation, the authors should state this explicitly. Otherwise, this comment should be removed.
The investigators chose to use linear spacing for the lambda values in all alchemical processes including the addition of harmonic restraints to the physical system. They also note that adding harmonic restraints represented the most time-intensive part of the overall workflow and required splitting into 6 different steps of increasing restraint strength. Furthermore, they find that the overlap between neighboring lambda states during the restraint addition is quite low (Figure 2-4) and produces large uncertainties in their final free energy estimates. In my own investigations of adding harmonic restraints to solids from 2016 (cited in this work) I observed that either cubically- or quartically- spaced lambda values significantly improve the overlap along the thermodynamic path relative to linear spacing and reduce the total amount of simulation cost. This should be included as a potential remedy for the high simulation cost lamented in the discussion section of the paper.
The investigators chose to use a large value of >1,000,000 kJ/nm/mol for their final restraint state to add or remove inter-particle interactions. It is necessary to have strong restraints in order to remove stiff degrees of freedom such as bonds and angles. However, it is possible that the interaction removal could be achieved with a weaker value of the restraint constant, and this would in turn reduce the number of simulations to add or remove harmonic restraints. This should also be discussed in the context of ways to reduce the amount of simulation expense observed for these calculations.
Finally, the authors should consider including the additional papers of Sellers et al. 2016¹ and Schilling and Schmid 2009² who also explore the use of atomistic simulation to compute absolute solid free energies. These articles also discuss how to apply restraints in a manner that preserves the indistinguishability of certain particles. It would be worth discussing ways to account for particle indistinguishablility in the method presented in this paper.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

References

Competing Interests

No competing interests were disclosed.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Reader Comment

04 Jan 2019

David Mobley

We've just submitted a revised version to deal with these comments, which we very much appreciate. I'll just respond to a couple of the comments here "for the record".

To your point 1:

We appreciate the your point that our use of this for “flexible” molecules (even if not particularly flexible) is potentially an extension of earlier work and have amended our manuscript accordingly. We also added a couple of sentences highlighting that this works on molecules which are somewhat flexible, though pointing out that the molecules here are not especially floppy and the method may not work as well on especially floppy molecules.

It's worth noting that our molecules are not as flexible as the word might imply. Acetylsalicylic acid is made of an aromatic ring bonded to a carboxyl group and an acetyl group in the ortho position. In the crystal structure the ring and the carboxyl group are rather rigid in the same plane -- there are hydrogen bonds between two ASA molecules forming a dimer -- and the only flexible part of the molecule is the acetyl group. EMM would probably not perform well if the crystal contained very floppy carbon chains -- butyl, pentyl, hexyl, and so on. On this case, since the “core” of the molecule is reasonably rigid and the acetyl group on the side rather fixed in a position due to the spacial arrangement.

To your point 3, as we discussed by e-mail, in this study, we chose the frozen reference in arbitrary manner. In principle the choice of reference atom does not matter. For acetylsalicylic acid we selected one of the carbon atoms in the aromatic ring. It is not uncommon in free energy calculations of various types, including binding free energy calculations, to have to make arbitrary choices in which atoms to restrain or other considerations, and several studies have demonstrated that such choices in practice are unimportant, so applying a similar approach here was not a cause for concern. We have not examined this issue carefully. The revision now addresses this.

To your point 4, the integrator is not very robust. It requires a lot of parameter-tweaking, as it was outlined in Aragonès et al. For methanol, the uncertainty is +- 0.09. For ASA, the uncertainty is +- 3 kT (an orientation change parameters need to be optimized for each case). We added a couple of sentences discussing this to the paper. Presumably this could be a point for future optimization.

We addressed all your other points by making changes/additions to the text, including a rather extensive new discussion for potential places for optimization.

View more View less

Competing Interests

None. The review was excellent.

Back to all reports

Reviewer Report

35 Views

25 Jun 2018 | for Version 1

Lillian T. Chong, Department of Chemistry, University of Pittsburgh, Pittsburgh, PA, USA

Anthony T. Bogetti, Department of Chemistry, University of Pittsburgh, Pittsburgh, PA, USA

35 Views Cite this report Responses(3)

Approved

Introduction section: This section could be re-framed to accentuate the positive, informative aspects of this manuscript’s results. For instance, it would be worth mentioning the fact that the new thermodynamic cycle employed in this study was able to enhance solubility calculations of the methanol system, an important feature of this manuscript that should be highlighted early on. In addition, the example of Norvir in the first paragraph could be shortened considerably, and similar shortening of the Introduction could be more effective in presenting the broader impacts of this study.
Theory section: This section would benefit from a clear definition of an Einstein crystal for life scientists at the very beginning. Also important would be to include early in the Theory section explanations of the ECM and EMM cycles and logically structuring the rest of the section from there, including more fundamental equations as needed. Also, it is not clear in equation (5) what is meant by averaging over the configurations of the initial state. Please clarify.
Distinctives of this Work section: It would be beneficial to remind the reader of the unique aspects of the EMM method over ECM since the implementation of this method is the novel in the manuscript.
Methods section, third paragraph: It was not clear to this reader which temperatures were used for the liquid simulations. Please clearly mention the temperatures. If the simulations were run at 4 K, then the authors should comment on the accuracy of the TIP3P water model at this very low temperature.
Discussion section, second to last paragraph: The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (3)

Reader Comment

28 Jun 2018

David Mobley

I also wanted to respond to this point:
> The authors mention that “with better force fields, perhaps accuracy could be improved.” Regarding “better force fields”, it would be worth mentioning two recent fixed-charge force fields, AMBER ff15ipq and AMBER ff15fb, that have been developed using sweeping optimizations of hundreds of parameters simultaneously using automated tools and could be worth considering before using more expensive polarizable force fields such as AMOEBA.

I agree that other force fields might be worth trying before switching to polarizable approaches. However, ff15ipq and ff15fb are protein/nucleic acid force fields and don't cover general small molecules. We ARE working on better general small molecule force fields, though, and hopefully some day we can try those.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Pudipeddi M, Serajuddin AT: Trends in solubility of polymorphs. J Pharm Sci. 2005; 94(5): 929–939. PubMed Abstract | Publisher Full Text

[2] 2. Bauer J, Spanton S, Henry R, et al.: Ritonavir: an extraordinary example of conformational polymorphism. Pharm Res. 2001; 18(6): 859–866. PubMed Abstract | Publisher Full Text

[3] 3. Motherwell WD, Ammon HL, Dunitz JD, et al.: Crystal structure prediction of small organic molecules: A second blind test. Acta Crystallogr B. 2002; 58(Pt 4): 647–661. PubMed Abstract | Publisher Full Text

[4] 4. Aaltonen J, Allesø M, Mirza S, et al.: Solid form screening--a review. Eur J Pharm Biopharm. 2009; 71(1): 23–37. PubMed Abstract | Publisher Full Text

[5] 5. Bardwell DA, Adjiman CS, Arnautova YA, et al.: Towards crystal structure prediction of complex organic compounds--a report on the fifth blind test. Acta Crystallogr B. 2011; 67(Pt 6): 535–551. PubMed Abstract | Publisher Full Text | Free Full Text

[6] 6. Braun DE, McMahon JA, Koztecki LH, et al.: Contrasting Polymorphism of Related Small Molecule Drugs Correlated and Guided by the Computed Crystal Energy Landscape. Cryst Growth Des. 2014; 14(4): 2056–2072. Publisher Full Text

[7] 7. Cruz-Cabeza AJ, Bernstein J: Conformational Polymorphism. Chem Rev. 2014; 114(4): 2170–2191. PubMed Abstract | Publisher Full Text

[8] 8. Neumann MA, van de Streek J, Fabbiani FP, et al.: Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening. Nat Commun. 2015; 6: 7793. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Beran GJ: Modeling Polymorphic Molecular Crystals with Electronic Structure Theory. Chem Rev. 2016; 116(9): 5567–5613. PubMed Abstract | Publisher Full Text

[10] 10. Llinàs A, Glen RC, Goodman JM: Solubility Challenge: Can You Predict Solubilities of 32 Molecules Using a Database of 100 Reliable Measurements? J Chem Inf Model. 2008; 48(7): 1289–1303. PubMed Abstract | Publisher Full Text

[11] 11. Hopfinger AJ, Esposito EX, Llinàs A, et al.: Findings of the Challenge To Predict Aqueous Solubility. J Chem Inf Model. 2009; 49(1): 1–5. PubMed Abstract | Publisher Full Text

[12] 12. Salahinejad M, Le TC, Winkler DA: Aqueous Solubility Prediction: Do Crystal Lattice Interactions Help? Mol Pharm. 2013; 10(7): 2757–2766. PubMed Abstract | Publisher Full Text

[13] 13. Palmer DS, Mitchell JB: Is Experimental Data Quality the Limiting Factor in Predicting the Aqueous Solubility of Druglike Molecules? Mol Pharm. 2014; 11(8): 2962–2972. PubMed Abstract | Publisher Full Text

[14] 14. Lusci A, Pollastri G, Baldi P: Deep architectures and deep learning in chemoinformatics: the prediction of aqueous solubility for drug-like molecules. J Chem Inf Model. 2013; 53(7): 1563–1575. PubMed Abstract | Publisher Full Text | Free Full Text

[15] 15. Schnieders MJ, Baltrusaitis J, Shi Y, et al.: The Structure, Thermodynamics and Solubility of Organic Crystals from Simulation with a Polarizable Force Field. J Chem Theory Comput. 2012; 8(5): 1721–1736. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Palmer DS, Llinàs A, Morao I, et al.: Predicting Intrinsic Aqueous Solubility by a Thermodynamic Cycle. Mol Pharm. 2008; 5(2): 266–279. PubMed Abstract | Publisher Full Text

[17] 17. Westergren J, Lindfors L, Höglund T, et al.: In silico prediction of drug solubility: 1. Free energy of hydration. J Phys Chem B. 2007; 111(7): 1872–1882. PubMed Abstract | Publisher Full Text

[18] 18. Lüder K, Lindfors L, Westergren J, et al.: In silico prediction of drug solubility: 2. Free energy of solvation in pure melts. J Phys Chem B. 2007; 111(7): 1883–1892. PubMed Abstract | Publisher Full Text

[19] 19. Lüder K, Lindfors L, Westergren J, et al.: In silico prediction of drug solubility. 3. Free energy of solvation in pure amorphous matter. J Phys Chem B. 2007; 111(25): 7303–7311. PubMed Abstract | Publisher Full Text

[20] 20. Lüder K, Lindfors L, Westergren J, et al.: In silico prediction of drug solubility: 4. Will simple potentials suffice? J Comput Chem. 2009; 30(12): 1859–1871. PubMed Abstract | Publisher Full Text

[21] 21. Ferrario M, Ciccotti G, Spohr E, et al.: Solubility of KF in water by molecular dynamics using the Kirkwood integration method. J Chem Phys. 2002; 117(10): 4947–4953. Publisher Full Text

[22] 22. Sanz E, Vega C: Solubility of KF and NaCl in water by molecular simulation. J Chem Phys. 2007; 126(1): 014507. PubMed Abstract | Publisher Full Text

[23] 23. Li L, Totton T, Frenkel D: Computational methodology for solubility prediction: Application to the sparingly soluble solutes. J Chem Phys. 2017; 146(21): 214110. PubMed Abstract | Publisher Full Text

[24] 24. Klimovich PV, Mobley DL: Predicting hydration free energies using all-atom molecular dynamics simulations and multiple starting conformations. J Comput Aided Mol Des. 2010; 24(4): 307–316. PubMed Abstract | Publisher Full Text

[25] 25. Shivakumar D, Williams J, Wu Y, et al.: Prediction of Absolute Solvation Free Energies using Molecular Dynamics Free Energy Perturbation and the OPLS Force Field. J Chem Theory Comput. 2010; 6(5): 1509–1519. PubMed Abstract | Publisher Full Text

[26] 26. Shivakumar D, Harder E, Damm W, et al.: Improving the Prediction of Absolute Solvation Free Energies Using the Next Generation OPLS Force Field. J Chem Theory Comput. 2012; 8(8): 2553–2558. PubMed Abstract | Publisher Full Text

[27] 27. Skyner RE, McDonagh JL, Groom CR, et al.: A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys Chem Chem Phys. 2015; 17(9): 6174–6191. PubMed Abstract | Publisher Full Text

[28] 28. Matos GDR, Kyu DY, Loeffler HH, et al.: Approaches for calculating solvation free energies and enthalpies demonstrated with an update of the FreeSolv database. J Chem Eng Data. 2017; 62(5): 1559–1569. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Boulanger E, Huang L, Rupakheti C, et al.: Optimized Lennard-Jones Parameters for Druglike Small Molecules. J Chem Theory Comput. 2018. PubMed Abstract | Publisher Full Text

[30] 30. Price SL: The computational prediction of pharmaceutical crystal structures and polymorphism. Adv Drug Deliv Rev. 2004; 56(3): 301–319. PubMed Abstract | Publisher Full Text

[31] 31. Day GM, Motherwell WD, Ammon HL, et al.: A third blind test of crystal structure prediction. Acta Crystallogr B. 2005; 61(Pt 5): 511–527. PubMed Abstract | Publisher Full Text

[32] 32. Woodley SM, Catlow R: Crystal structure prediction from first principles. Nat Mater. 2008; 7(12): 937–46. PubMed Abstract | Publisher Full Text

[33] 33. Day GM, Cooper TG, Cruz-Cabeza AJ, et al.: Significant progress in predicting the crystal structures of small organic molecules--a report on the fourth blind test. Acta Crystallogr B. 2009; 65(Pt 2): 107–125. PubMed Abstract | Publisher Full Text

[34] 34. Price SS: Computed crystal energy landscapes for understanding and predicting organic crystal structures and polymorphism. Acc Chem Res. 2009; 42(1): 117–126. PubMed Abstract | Publisher Full Text

[35] 35. Reilly AM, Cooper RI, Adjiman CS, et al.: Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr B Struct Sci Cryst Eng Mater. 2016; 72(Pt 4): 439–459. PubMed Abstract | Publisher Full Text | Free Full Text

[36] 36. Chipot C, Pohorille A: Free Energy Calculations Theory and Applications in Chemistry and Biology. Springer, 2007. Publisher Full Text

[37] 37. Chipot C: Frontiers in free-energy calculations of biological systems. WIREs Comput Mol Sci. 2014; 4(1): 71–89. Publisher Full Text

[38] 38. Shirts MR, Mobley DL, Chodera JD: Alchemical Free Energy Calculations: Ready for Prime Time? In DC. Spellmeyer and R. Wheeler, editors, Annu Rep Comput Chem. Elsevier. 2007; 3: 41–59. Publisher Full Text

[39] 39. Kirkwood JG: Statistical Mechanics of Fluid Mixtures. J Chem Phys. 1935; 3(5): 300–313. Publisher Full Text

[40] 40. Ytreberg FM, Swendsen RH, Zuckerman DM: Comparison of free energy methods for molecular systems. J Chem Phys. 2006; 125(18): 184114. PubMed Abstract | Publisher Full Text

[41] 41. Shirts MR, Pande VS: Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J Chem Phys. 2005; 122(14): 144107. PubMed Abstract | Publisher Full Text

[42] 42. Paliwal H, Shirts MR: A Benchmark Test Set for Alchemical Free Energy Transformations and Its Use to Quantify Error in Common Free Energy Methods. J Chem Theory Comput. 2011; 7(12): 4115–4134. PubMed Abstract | Publisher Full Text

[43] 43. Zwanzig RW: High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J Chem Phys. 1954; 22(8): 1420–1426. Publisher Full Text

[44] 44. Bennett CH: Efficient estimation of free energy differences from Monte Carlo data. J Comp Phys. 1976; 22(2): 245–268. Publisher Full Text

[45] 45. Wu D, Kofke DA: Asymmetric bias in free-energy perturbation measurements using two Hamiltonian-based models. Phys Rev E Stat Nonlin Soft Matter Phys. 2004; 70(6 Pt 2): 066702. PubMed Abstract | Publisher Full Text

[46] 46. Wu D, Kofke DA: Phase-space overlap measures. I. Fail-safe bias detection in free energies calculated by molecular simulation. J Chem Phys. 2005; 123(5): 54103. PubMed Abstract | Publisher Full Text

[47] 47. Frenkel D, Ladd AJC: New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres. J Chem Phys. 1984; 81(7): 3188–3193. Publisher Full Text

[48] 48. Vega C, Sanz E, Abascal JLF, et al.: Determination of phase diagrams via computer simulation: Methodology and applications to water, electrolytes and proteins. J Phys Condens Matter. 2008; 20(15): 153101. Publisher Full Text

[49] 49. Noya EG, Conde MM, Vega C: Computing the free energy of molecular solids by the Einstein molecule approach: ices XIII and XIV, hard-dumbbells and a patchy model of proteins. J Chem Phys. 2008; 129(10): 104704. PubMed Abstract | Publisher Full Text

[50] 50. Vega C, Noya EG: Revisiting the Frenkel-Ladd method to compute the free energy of solids: the Einstein molecule approach. J Chem Phys. 2007; 127(15): 154113. PubMed Abstract | Publisher Full Text

[51] 51. Aragones JL, Sanz E, Vega C: Solubility of NaCl in water by molecular simulation revisited. J Chem Phys. 2012; 136(24): 244508. PubMed Abstract | Publisher Full Text

[52] 52. Aragones JL, Noya EG, Valeriani C, et al.: Free energy calculations for molecular solids using GROMACS. J Chem Phys. 2013; 139(3): 034104. PubMed Abstract | Publisher Full Text

[53] 53. Ben-Naim A: Molecular Theory of Solutions. Oxford University Press, Oxford, 2006. Reference Source

[54] 54. Mobley DL, Guthrie JP: FreeSolv: a database of experimental and calculated hydration free energies, with input files. J Comput Aided Mol Des. 2014; 28(7): 711–720. PubMed Abstract | Publisher Full Text | Free Full Text

[55] 55. Benavides AL, Aragones JL, Vega C: Consensus on the solubility of NaCl in water from computer simulations using the chemical potential route. J Chem Phys. 2016; 144(12): 124504. PubMed Abstract | Publisher Full Text

[56] 56. Park J, Nessler I, McClain B, et al.: Absolute Organic Crystal Thermodynamics: Growth of the Asymmetric Unit into a Crystal via Alchemy. J Chem Theory Comput. 2014; 10(7): 2781–2791. PubMed Abstract | Publisher Full Text

[57] 57. Kim Y, Machida K, Taga T, et al.: Structure redetermination and packing analysis of aspirin crystal. Chem Pharm Bull (Tokyo). 1985; 33(7): 2641–2647. PubMed Abstract | Publisher Full Text

[58] 58. Yalkowsky SH, He Y, Jain P: Handbook of Aqueous Solubility Data. CRC Press, second edition, 2010. Reference Source

[59] 59. Henshaw DG: Atomic Distribution in Liquid and Solid Neon and Solid Argon by Neutron Diffraction. Phys Rev. 1958; 111(6): 1470–1475. Publisher Full Text

[60] 60. Berendsen HJC, van der Spoel D, van Drunen R: GROMACS: A message-passing parallel molecular dynamics implementation. Comput Phys Comm. 1995; 91(1): 43–56. Publisher Full Text

[61] 61. Van Der Spoel D, Lindahl E, Hess B, et al.: GROMACS: fast, flexible, and free. J Comput Chem. 2005; 26(16): 1701–1718. PubMed Abstract | Publisher Full Text

[62] 62. Hess B, Kutzner C, van der Spoel D, et al.: GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J Chem Theory Comput. 2008; 4(3): 435–447. PubMed Abstract | Publisher Full Text

[63] 63. Pronk S, Páll S, Schulz R, et al.: GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013; 29(7): 845–854. PubMed Abstract | Publisher Full Text | Free Full Text

[64] 64. Jakalian A, Bush BL, Jack DB, et al.: Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J Comput Chem. 2000; 21(2): 132–146. Publisher Full Text

[65] 65. Jakalian A, Jack DB, Bayly CI: Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J Comput Chem. 2002; 23(16): 1623–1641. PubMed Abstract | Publisher Full Text

[66] 66. Parrinello M, Rahman A: Polymorphic transitions in single crystals: A new molecular dynamics method. J Appl Phys. 1981; 52(12): 7182. Publisher Full Text

[67] 67. Jorgensen WL, Chandrasekhar J, Madura JD, et al.: Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983; 79(2): 926–935. Publisher Full Text

[68] 68. Macrae CF, Edgington PR, McCabe P, et al.: Mercury: Visualization and analysis of crystal structures. J Appl Cryst. 2006; 39(3): 453–457. Publisher Full Text

[69] 69. Case DA, Cheatham TE 3rd, Darden T, et al.: The Amber biomolecular simulation programs. J Comput Chem. 2005; 26(16): 1668–1688. PubMed Abstract | Publisher Full Text | Free Full Text

[70] 70. Salomon-Ferrer R, Case DA, Walker RC: An overview of the Amber biomolecular simulation package. WIREs Comput Mol Sci. 2013; 3(2): 198–210. Publisher Full Text

[71] 71. Cheatham TE 3rd, Case DA: Twenty-five years of nucleic acid simulations. Biopolymers. 2013; 99(12): 969–977. PubMed Abstract | Publisher Full Text | Free Full Text

[72] 72. Case DA, Babin V, Berryman JT, et al.: Amber 14. 2014. Reference Source

[73] 73. Swails J, Hernandez C, Mobley DL, et al.: Parmed. (accessed October 9, 2015).

[74] 74. Shirts MR, Chodera JD: Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys. 2008; 129(12): 124105. PubMed Abstract | Publisher Full Text | Free Full Text

[75] 75. Klimovich PV, Mobley DL: A Python tool to set up relative free energy calculations in GROMACS. J Comput Aided Mol Des. 2015; 29(11): 1007–1014. PubMed Abstract | Publisher Full Text | Free Full Text

[76] 76. de Ruiter A, Boresch S, Oostenbrink C: Comparison of thermodynamic integration and Bennett acceptance ratio for calculating relative protein-ligand binding free energies. J Comp Chem. 2013; 34(12): 1024–1034. PubMed Abstract | Publisher Full Text

[77] 77. Bannan CC, Calabró G, Kyu DY, et al.: Calculating Partition Coefficients of Small Molecules in Octanol/Water and Cyclohexane/Water. J Chem Theory Comp. 2016; 12(8): 4015–4024. PubMed Abstract | Publisher Full Text | Free Full Text

[78] 78. Martínez L, Andrade R, Birgin EG, et al.: PACKMOL: a package for building initial configurations for molecular dynamics simulations. J Comp Chem. 2009; 30(13): 2157–2164. PubMed Abstract | Publisher Full Text

[79] 79. Beauchamp KA, Rustenburg AS, Rizzi A, et al.: OpenMolTools.

[80] 80. Inc: OpeneEye Scientific Software. OEChem Toolkit, 2010; (accessed June 16, 2015).

[81] 81. Inc: OpeneEye Scientific Software. QUACPAC 1.7.0.2.

[82] 82. Hawkins PC, Nicholls A: Conformer generation with OMEGA: learning from the data set and the analysis of failures. J Chem Inf Model. 2012; 52(11): 2919–2936. PubMed Abstract | Publisher Full Text

[83] 83. Frenkel D, Smit B: Understanding Molecular Simulation: From Algorithms to Applications. Academic Press Inc. (London) Ltd., 1996; 1. Reference Source

[84] 84. Pohorille A, Jarzynski C, Chipot C: Good Practices in Free-Energy Calculations. J Phys Chem B. 2010; 114(32): 10235–10253. PubMed Abstract | Publisher Full Text

[85] 85. Klimovich PV, Shirts MR, Mobley DL: Guidelines for the analysis of free energy calculations. J Comput Aided Mol Des. 2015; 29(5): 397–411. PubMed Abstract | Publisher Full Text | Free Full Text

[86] 86. Mobley DL, Dumont E, Chodera JD, et al.: Comparison of charge models for fixed-charge force fields: small-molecule hydration free energies in explicit solvent. J Phys Chem B. 2007; 111(9): 2242–2254. PubMed Abstract | Publisher Full Text

[87] 87. Fennell CJ, Wymer KL, Mobley DL: A fixed-charge model for alcohol polarization in the condensed phase, and its role in small molecule hydration. J Phys Chem B. 2014; 118(24): 6438–6446. PubMed Abstract | Publisher Full Text | Free Full Text

[88] 88. Kramer C, Spinn A, Liedl KR: Charge Anisotropy: Where Atomic Multipoles Matter Most. J Chem Theory Comput. 2014; 10(10): 4488–4496. PubMed Abstract | Publisher Full Text

[89] 89. Eike DM, Brennecke JF, Maginn EJ: Toward a robust and general molecular simulation method for computing solid-liquid coexistence. J Chem Phys. 2005; 122(1): 14115. PubMed Abstract | Publisher Full Text

[90] 90. Eike DM, Maginn EJ: Atomistic simulation of solid-liquid coexistence for molecular systems: application to triazole and benzene. J Chem Phys. 2006; 124(16): 164503. PubMed Abstract | Publisher Full Text

[91] 91. Paluch AS, Jayaraman S, Shah JK, et al.: A method for computing the solubility limit of solids: application to sodium chloride in water and alcohols. J Chem Phys. 2010; 133(12): 124504. PubMed Abstract | Publisher Full Text

[92] 92. Dybeck EC, Schieber NP, Shirts MR: Effects of a More Accurate Polarizable Hamiltonian on Polymorph Free Energies Computed Efficiently by Reweighting Point-Charge Potentials. J Chem Theory Comput. 2016; 12(8): 3491–3505. PubMed Abstract | Publisher Full Text

Challenges in the use of atomistic simulations to predict solubilities of drug-like molecules

Abstract

Keywords

Introduction

Theory

The solubility of a molecular solid is related to the chemical potentials of each phase

Alchemical free energy calculations can be used to calculate absolute free energies

The absolute free energy of a solid is calculated using an ideal system as reference

Figure 1.

The chemical potential of a component of a solution can be calculated using free energy calculations

Distinctives of this work

Methods

Systems under study

Calculation of the absolute free energy of molecular crystals

Chemical potential calculations

Results

Chemical potential of molecular solids

Figure 2. Phase space overlap between the states in a thermodynamic path for removing restraints with λ.

Figure 3. Phase space overlap between the states in the path between IEM and the α-methanol solid.

Figure 4. Phase space overlap between the states in the path between IEM and the fcc argon solid.

Table 1. Absolute free energy components for α-methanol at 150 K, in kBT.

Table 2. Absolute free energy components for polymorph I of acetylsalicylic acid (ASA) at 298.15 K, in kBT.

Chemical potential of solutions and the solubility of GAFF ASA in TIP3P water

Table 3. Standard chemical potential of acetylsalicylic acid (ASA) at 298.15 K, in kBT.

Table 4. Simulation data for solutions of acetylsalicylic acid in water in different concentrations.

Figure 5. Chemical potentials of ASA, solid and solution in different concentrations, with respect to mole fraction.

Discussion

Data availability

Competing interests

Grant information

Acknowledgements

Supplementary material

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Table 1. Absolute free energy components for α-methanol at 150 K, in k_BT.

Table 2. Absolute free energy components for polymorph I of acetylsalicylic acid (ASA) at 298.15 K, in k_BT.

Table 3. Standard chemical potential of acetylsalicylic acid (ASA) at 298.15 K, in k_BT.