ccbmlib

Martin Vogt; Jürgen Bajorath

doi:10.12688/f1000research.22292.1

Home Browse ccbmlib – a Python package for modeling Tanimoto similarity value...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

ccbmlib – a Python package for modeling Tanimoto similarity value distributions

[version 1; peer review: 2 approved]

Martin Vogt¹, Jürgen Bajorath ¹

PUBLISHED 10 Feb 2020

Author details Author details

¹ Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, NRW, 53115, Germany

Martin Vogt
Roles: Conceptualization, Data Curation, Formal Analysis, Methodology, Software, Writing – Original Draft Preparation

Jürgen Bajorath
Roles: Conceptualization, Methodology, Supervision, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Cheminformatics gateway.

This article is included in the Python collection.

This article is included in the Mathematical, Physical, and Computational Sciences collection.

Abstract

The ccbmlib Python package is a collection of modules for modeling similarity value distributions based on Tanimoto coefficients for fingerprints available in RDKit. It can be used to assess the statistical significance of Tanimoto coefficients and evaluate how molecular similarity is reflected when different fingerprint representations are used. Significance measures derived from p-values allow a quantitative comparison of similarity scores obtained from different fingerprint representations that might have very different value ranges. Furthermore, the package models conditional distributions of similarity coefficients for a given reference compound. The conditional significance score estimates where a test compound would be ranked in a similarity search. The models are based on the statistical analysis of feature distributions and feature correlations of fingerprints of a reference database. The resulting models have been evaluated for 11 RDKit fingerprints, taking a collection of ChEMBL compounds as a reference data set. For most fingerprints, highly accurate models were obtained, with differences of 1% or less for Tanimoto coefficients indicating high similarity.

Keywords

Bernoulli model, fingerprints, p-value, similarity value distributions, Tanimoto coefficient.

Corresponding author: Jürgen Bajorath

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2020 Vogt M and Bajorath J. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Vogt M and Bajorath J. ccbmlib – a Python package for modeling Tanimoto similarity value distributions [version 1; peer review: 2 approved]. F1000Research 2020, 9(Chem Inf Sci):100 (https://doi.org/10.12688/f1000research.22292.1) First published: 10 Feb 2020, 9(Chem Inf Sci):100 (https://doi.org/10.12688/f1000research.22292.1) Latest published: 05 Mar 2020, 9(Chem Inf Sci):100 (https://doi.org/10.12688/f1000research.22292.2)

Introduction

The quantitative assessment of molecular similarity is a central concept in chemoinformatics^1–4. It forms the basis of similarity searching and ligand-based virtual screening to identify novel molecules in large databases with biological properties similar to given reference compounds^5–7. Assessment of molecular similarity plays a central role in chemical space analysis and the study of activity landscapes where chemical space projections onto low-dimensional representations are based on quantified similarities^8,9.

The use of fingerprints and the Tanimoto coefficient¹⁰ (Tc), also known as the Jaccard index¹¹, represents one of the most popular methods for quantifying molecular similarity^1–4. Fingerprints encode structural features of a molecule in a binary vector format and the Tc quantifies the overlap of features of two molecules as the ratio of the number of common features to the total number of features in each fingerprint. The Tc has the value range 0 to 1 and can be interpreted as the percentage of features shared by two molecules. However, whether a given percentage of overlap should be considered a significant similarity of two molecules depends on the fingerprint design and the global frequency of encoded features. Fingerprint designs might be categorized as dense or sparse. Dense fingerprints have a relatively small dimensionality of at most a few thousand features, but a significant fraction of these might be present in any given molecule. On the other hand, sparse fingerprints can have a theoretically infinite set of features (typical integer encodings allow up to 4 billion features). However, only tens or hundreds of these features might be found in a single molecule. Consequently, sparse fingerprint representations generally lead to smaller Tc values than dense fingerprints.

While it is not meaningful to compare Tc values of different fingerprint designs directly, statistical approaches can be applied to assess the significance of Tc values with respect to a reference data set. By using the distribution of Tc values obtained from comparing random compounds as a reference, Tc value significance can be determined by calculating the probability of obtaining a given Tc or higher value by chance. In statistical terms, the reference distribution corresponds to a null hypothesis and the significance measure is known as p-value or p-score. This score has the range 0 to 1 and indicates the probability that a given Tc would be obtained by chance. Thus, smaller p-values indicate higher significance. Here, we will use the measure 1 – (p-value) to assess significance. Although it is in principle possible to obtain Tc distributions by random sampling, this process is time consuming. Instead, the ccbmlib package presented here provides methods for the generation of Tc distribution models that are based on the statistical analysis of feature frequencies and feature correlations between fingerprints for a reference data set. Some mathematical models of Tc-value distributions^12–14 have been introduced in the past. The ccbmlib implementation makes use of the conditional correlated Bernoulli model (CCBM) that has been shown to accurately model Tc distributions for a variety of fingerprint designs^13,14. An unconditional distribution model accounts for Tc distributions of fingerprints of randomly selected compounds. However, it is of particular interest to model distributions where one compound fingerprint is used as a reference, which forms the basis of similarity searching. P-values obtained from such conditional distribution models efficiently estimate how high a test compound would be ranked in a similarity search with respect to a given reference compound. Hence, conditional models can be used to predict similarity search performance^13,14.

The implementation presented here is based on RDKit¹⁵ and provides methods for statistically analyzing fingerprint feature distributions and building models for fingerprints implemented in RDKit. Methods are provided for calculating significance from Tc values, which enable a meaningful comparison of Tc values calculated using fingerprints of different design. The CCBM requires knowledge of the frequency of individual features as well as their pairwise covariances. This statistical analysis needs to be carried out once for each reference data set and fingerprint design. This step can be time consuming for large data sets. The ccbmlib implementation stores resulting statistics permanently to avoid redundant calculations. For our reference implementation and evaluation, compounds from ChEMBL (release 25)¹⁶ were selected as a representative sample of bioactive chemical space.

Methods

Fingerprint representations

RDKit provides implementations for a variety of fingerprints. Available fingerprints are reported in Table 1. The atom pair fingerprint encodes typed pairs of atoms and their bond distance and is based on the description given by Carhart and Smith¹⁷, representing a sparse fingerprint. The Avalon fingerprint¹⁸ is a hashed fingerprint enumerating paths and feature classes. MACCS (Molecular ACCess System) keys record the presence or absence of a dictionary of 166 substructural features¹⁹. Morgan fingerprints are an RDKit implementation of extended connectivity fingerprints (ECFPs)²⁰ and enumerate atom environments up to a selected radius. We calculated Morgan fingerprints for radius 1 and 2 corresponding to ECFP with diameter 2 and 4, respectively. The topological torsion fingerprints encode sequences of four bonded atoms in a sparse fingerprint²¹. The RDKit fingerprint is a hashed substructure/path fingerprint similar to the Daylight fingerprints²². Atom pairs, Morgan fingerprints, and the topological torsion fingerprint result in sparse vector representations whose dimensions are only limited by the underlying numerical representation. Hashing is often used to yield a dense fingerprint representation of constant length. We evaluated our models using the sparse and hashed versions with a default size of 2048 bits.

Table 1. Fingerprints available in RDKit.

Fingerprint	Dimension	Description	μ(FC)	σ(FC)
Atom pairs	sparse	typed atom pairs	199.8	155.9
Atom pairs – hashed	2048		186.3	126.4
Avalon	512	path-based	206.3	78.9
MACCS keys	166	substructures	52.1	13.5
Morgan radius 1	sparse	atom environments	30.5	8.4
Morgan radius 1 – hashed	2048		30.1	8.2
Morgan radius 2	sparse		51.0	15.3
Morgan radius 2 – hashed	2048		50.3	14.9
Topological torsions	sparse	4-atom-paths	34.7	13.8
Topological torsions – hashed	2048		34.2	13.4
RDKit	2048	path-based	877.5	324.0

μ(FC) and σ(FC) are the average number and standard deviation of the number of features per fingerprint for ChEMBL compounds, respectively.

For the following mathematical description of the models, we will use lowercase bold letters to indicate bit vector representations and uppercase italic symbols to denote the corresponding feature set representations:

\begin{matrix} a = (a_{1}, a_{2}, \dots, a_{d}) where a_{i} \in {0, 1}, 1 \leq i \leq d \\ A = {i | a_{i} = 1, 1 \leq i \leq d} \end{matrix} (1)

Here, d ∈ ℕ is the dimension of the fingerprint.

Fingerprint similarity

Similarity of fingerprints is most often assessed on the basis of the set of features common to two fingerprints. The Tanimoto coefficient^10,11 is defined as the ratio of the number of features common to two fingerprints A and B to the total number of features present in either A or B:

T c (A, B) = \frac{| A \cap B |}{| A \cup B |} = \frac{I (A, B)}{U (A, B)} (2)

where I(A, B) = |A ∩ B| and U(A, B) = |A ∪ B| are the cardinalities of the intersection and union of A and B, respectively.

Modeling similarity value distributions

The distribution of Tc values depends on the fingerprints of a reference compound data set. The resulting p-values must be interpreted with respect to the reference data set.

As indicated in Equation 1, fingerprints can be represented as sets of features and similarity metrics like the Tc depend on the cardinalities of the intersection and union of sets. Each of the d features X_i of a fingerprint can be modeled as a Bernoulli variable that occurs with a certain probability p_i. Given a reference data set of N compounds and their fingerprints A = {a_k|1 ≤ k ≤ N} where a_k = (a_j1, a_j2, … a_jd) the probabilities can be estimated from the relative frequencies:

p_{i} = E (X_{i}) = \frac{1}{N} Σ_{k = 1}^{N} a_{k i}, 1 \leq i \leq d (3)

The cardinality of a fingerprint itself, of the intersection, and of the union can then be modeled as a sum of non-identically distributed Bernoulli variables. In the case of independent variables, the sum follows a Poisson binomial distribution with mean

μ = Σ_{i = 1}^{d} p_{i} (4)

and variance

σ^{2} = Σ_{i = 1}^{d} p_{i} (1 – p_{i}) (5)

and can be approximated by a normal distribution. Because the cardinalities of the intersection and union of two sets are not independent, the Tc is then modeled as the ratio of two correlated normal distributions for which approximations exist^23,24.

Fingerprint features are often correlated. Ignoring these correlations leads to a significant underestimation of the variance (Equation 5)^13,14. While the equation for the mean μ remains valid for correlated random variables, the formula for the variance σ² requires taking the pairwise covariances c_ij = cov(X_i,X_j) between the different features into account. These can also be estimated from the reference set:

c_{i j} = E ((X_{i} - p_{i}) (X_{j} - p_{j})) = E (X_{i} X_{j}) - p_{i} p_{j} = \frac{1}{N} Σ_{k = 1}^{N} a_{k i} a_{k j} - p_{i} p_{j} (6)

Accordingly, the value c_ii = p_i (1 – p_i) denotes the variance of X_i.

Based on these estimates, the average cardinality of a fingerprint itself, of the intersection, and of the union of two unknown fingerprints can be determined:

E (| X |) = Σ_{i = 1}^{d} p_{i} (7)

μ_{I} = E (I (X, Y)) = Σ_{i = 1}^{d} p_{i}^{2} (8)

μ_{U} = E (U (X, Y)) = E (| X | + | Y | - I (X, Y)) = 2 Σ_{i = 1}^{d} p_{i} - Σ_{i = 1}^{d} p_{i}^{2} (9)

For the respective variances, one obtains:

Var (| X |) = Σ_{i = 1}^{d} Σ_{j = 1}^{d} c_{i j} (10)

σ_{I}^{2} = Var (I (X, Y)) = Σ_{i = 1}^{d} Σ_{j = 1}^{d} (c_{i j}^{2} + 2 c_{i j} p_{i} p_{j}) (11)

σ_{U}^{2} = Var (U (X, Y)) = Σ_{i = 1}^{d} Σ_{j = 1}^{d} 2 c_{i j} (1 - 2 p_{j}) + σ_{I}^{2} (12)

The covariance between the cardinality of union and intersection is given by:

{cov}_{I U} = Cov (I (X, Y), U (X, Y)) = Σ_{i = 1}^{d} Σ_{j = 1}^{d} 2 c_{i j} p_{j} - σ_{I}^{2} (13)

Normal distributions are defined by their mean and standard deviation and can thus be calculated from the estimates of the averages and variances. However, given the fact that the underlying features are not independent, the suitability of using normal distributions as approximations cannot be guaranteed from a theoretical point of view. Nevertheless, as has been previously shown^13,14, and as can be seen from our current evaluation (vide infra), practical applications of the model yield good performance for a variety of different fingerprint designs. Under the assumption of normality, the following models are obtained:

I (X, Y) \approx N (μ_{I}, σ_{I}^{2}) (14)

U (X, Y) \approx N (μ_{U}, σ_{U}^{2}) (15)

where N(μ,σ²) is the normal distribution with mean μ and standard deviation σ. The Tc distribution is then modeled as a ratio of these two correlated distributions. An analytical form of the probability distribution function exists²³; however, for determining p-values and the significance, the following approximation of the cumulative distribution function (CDF) is used²⁴:

F (t) \approx Φ (\frac{μ_{U} t - μ_{I}}{σ_{I} σ_{U} a (t)}) where a (t) = \sqrt{\frac{t^{2}}{σ_{I}^{2}} - \frac{2 ρ t}{σ_{I} σ_{U}} - \frac{1}{σ_{U}^{2}}} (16)

Here, ρ = cov_IU / (σ_Iσ_U) is the correlation between intersection and union and Φ is the CDF of the standard normal distribution:

Φ (u) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{u} \exp (- \frac{x^{2}}{2}) d x (17)

The p-value can then be determined as:

p = 1 - F (t) = Pr (Tc > t) (18)

For model evaluation, we use F(t) = Pr (Tc ≤ t) directly as an indication of significance.

Modeling conditional value distributions

For similarity searching, reference compounds are used and Tc values of database compounds are calculated relative to the references. As has been shown¹³, distributions of Tc values can vary greatly depending on the reference fingerprint. In this case, the significance of Tc values should to be considered for a given reference compound. Mathematically, this corresponds to determining the conditional distributions when one fingerprint is given. As in the unconditional case, the distributions are based on sums of correlated Bernoulli variables that are modeled as normal distributions based on the conditional means and variances:

μ_{I}^{A} = E (I (A, X) | A) = Σ_{i \in A} p_{i} (19)

μ_{U}^{A} = E (U (A, X) | A) = E (| A | + Σ_{i \notin A} X_{i}) = | A | + Σ_{i \notin A} p_{i} (20)

{(σ_{I}^{A})}^{2} = Var (I (A, X) | A) = Σ_{i, j \in A} c_{i j} (21)

{(σ_{U}^{A})}^{2} = Var (U (A, X) | A) = Σ_{i, j \notin A} c_{i j} (22)

{cov}_{IU}^{A} = cov (I (A, X), U (A, X) | A) = Σ_{i \in A} Σ_{j \notin A} c_{i j} (23)

The conditional model is obtained by applying these parameters in Equation 16.

A derivation of the formulas presented here for the CCBM can be found in the original publications^13,14.

Sparse fingerprints

Sparse fingerprints like ECFPs or the Morgan fingerprint might result in hundreds of thousands of different features present in large data sets. Most of these will occur with very small probabilities p_i and only have a small influence on the estimated means and variances. It is computationally unproblematic to handle these individual probability estimates; however, determining pairwise covariances of all possible features becomes infeasible for more than a few thousand features. To address this issue, the complete covariance matrix is only determined for the most frequent features of a sparse fingerprint (by default, the 2048 most frequent features are selected). Covariances involving rare fingerprints are not estimated. Given that feature probabilities of combinatorial fingerprints usually show pseudo-exponential drop-offs for rare features, contributions towards covariance estimates have negligible influence on the final estimates and are ignored in the current implementation.

Data sets

As reference data set, ChEMBL compounds were selected. SMILES representations of 1,870,461 compounds were downloaded and standardized using a previously published protocol included in the ccbmlib package²⁵. Additionally, stereochemical information was removed since most fingerprints implemented in RDKit do not account for stereochemistry, resulting in 1,691,786 unique compounds. Fingerprint statistics are reported in Table 1.

Implementation and operation

The software has been implemented as a module for Python 3.7. It requires the installation of RDKit and has been tested with version 2019.03.4 of RDKit. Any system (Linux, Windows, MacOS) capable of running Python 3.7 and RDKit is sufficient for running our software. A 64-bit operating system with at least 8GB RAM is recommended. After obtaining the code it can be installed using Python’s setup utility. The ccbmlib package contains three modules: preprocessing, statistics, and models.

Module preprocessing consists of routines for standardizing molecules and preparing compound data sets. Standardization of molecules is a generally recommended preprocessing step, especially when compound data sets are assembled from different sources.

Module statistics contains classes for feature statistics and distribution models. Its main classes are PairwiseStats and CorrelatedNormalDistributions for the fingerprint statistics and distribution models, respectively. Distribution models are obtained from PairwiseStats objects using the get_tc_distribution method, which are used to generate unconditional and conditional models.

The module models provides the main interface for the package. It offers wrapper functions for calculating RDKit fingerprints and contains the central method get_feature_statistics for generating or retrieving fingerprint statistics for a reference data set. Once calculated, statistics are saved and can be retrieved for later use. Exemplary applications of the module are provided in the readme file of the ccbmlib distribution.

Results and discussion

Fingerprint statistics were calculated on the basis of the 1,691,786 unique ChEMBL compounds and distribution models were derived. To evaluate the quality of the general model, 1,000,000 Tc values were calculated from pairs of random compounds drawn from the ChEMBL data set and empirical CDFs were determined. Figure 1 compares the empirical CDFs to the modeled unconditional CDFs for the fingerprints in Table 1. Overall, the modeled CDFs match the different value ranges and shapes of the empirical CDFs very well. However, to assess the usefulness of the model as a quantitative and comparative tool, the quality of the model should be assessed with a focus on Tc values indicating high significance. The insets of the figures show an enlarged section with Tc values having a significance of 0.9 or higher. The models for the atom pair fingerprints are not able to accurately model the distribution in this region. However, most other Tc distributions can be modeled very well. For the MACCS, Morgan, and topological torsion fingerprint distributions, high-quality models are obtained with small differences between the theoretical and empirical model. The hashed variants of the Morgan and topological torsion fingerprints have distributions highly similar to their sparse counterparts. This can be expected because the average feature counts reported in Table 1 are also very similar, indicating that most of the sparse features are hashed to unique values and only few collisions occur between hashed values. The path-based Avalon and RDKit fingerprints still have usable, although less accurate models. These observations are consistent with previous observations¹³. CCBM models pharmacophore-based fingerprints only to a limited extent. This might be due to the specific nature of correlations between pharmacophore features.

Figure 1. Empirical and modeled cumulative distribution functions.

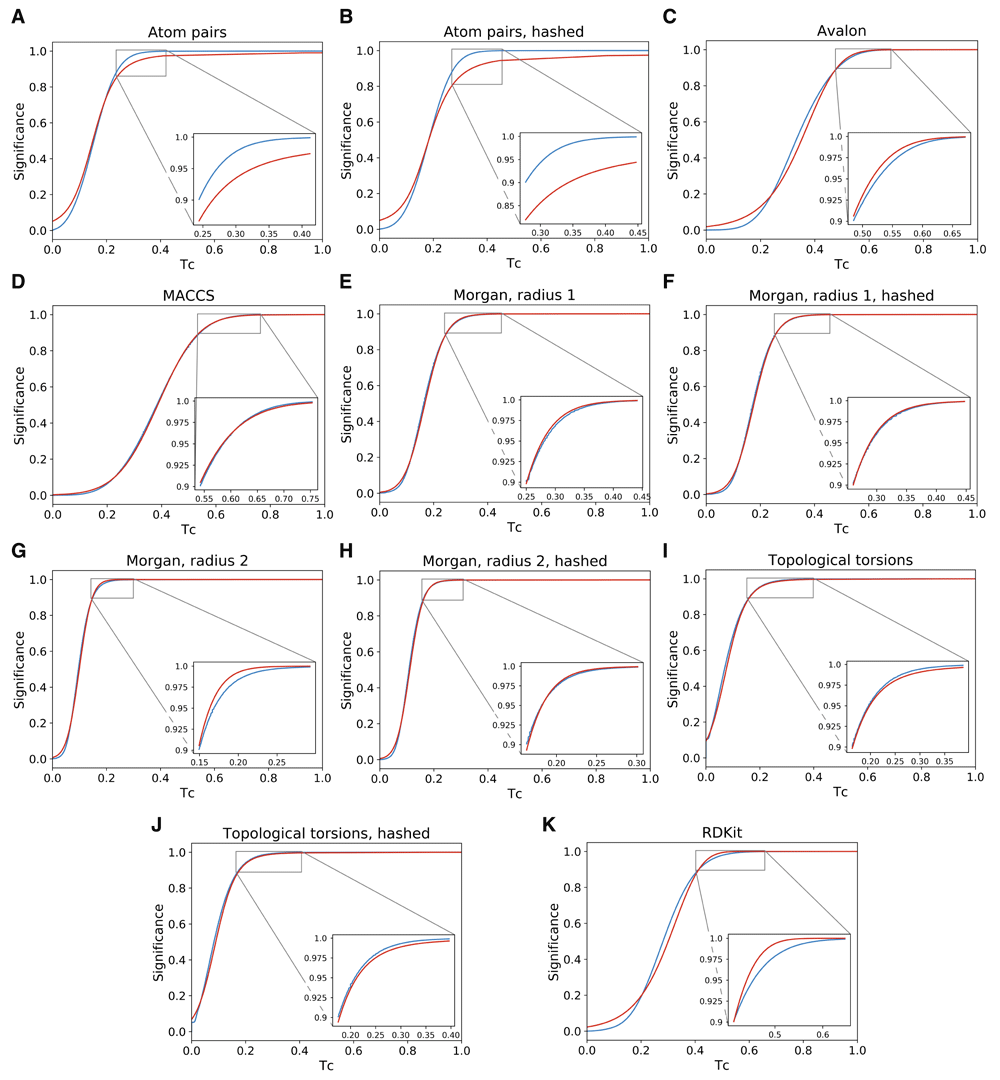
The empirical and modeled cumulative distribution functions for the fingerprints reported in Table 1 are shown in (a) – (k). Blue lines indicate empirical distributions obtained from randomly sampling 1,000,000 pairs of compounds from ChEMBL. Red lines show the corresponding modeled distributions according to Equation (16). The inserts highlight the correspondence between the curves for Tc values of high significance.

A quantitative summary of the observations is given in Table 2. It reports the Kolmogorov-Smirnov statistic (KS)²⁶, which is defined as the maximum difference between empirical (F_emp) and modeled (F_model) distributions:

KS (F_{emp}, F_{model}) = \max_{x} | F_{emp} (x) - F_{model} (x) | (24)

Table 2. Kolmogorov-Smirnov statistics.

Fingerprint	KS	KS₉₀
Atom pairs	5.47%	4.22%
Atom pairs – hashed	8.80%	8.80%
Avalon	6.91%	1.04%
MACCS	2.09%	0.43%
Morgan radius 1	3.64%	0.54%
Morgan radius 1 – hashed	3.37%	0.30%
Morgan radius 2	4.16%	1.26%
Morgan radius 2 – hashed	3.80%	0.83%
Topological torsions	9.31%	0.47%
Topological torsions – hashed	6.78%	0.75%
RDKit	8.03%	1.70%

KS reports the Kolmogorov-Smirnov statistic comparing the experimental to the modeled distributions. KS₉₀ reports the Kolmogorov-Smirnov statistic limited to Tc values with an empirical significance of at least 90%.

In addition, the maximum difference for the significance range beyond 90% is reported (KS₉₀):

{KS}_{90} (F_{emp}, F_{model}) = \max_{x} | F_{emp} (x) - F_{model} (x) | (25)

The maximum difference for most models is observed for common Tc values, i.e., where the slope of the CDF is steepest. However, as can be seen from the KS₉₀ values, the high significance range can be accurately assessed within 1% for MACCS, most Morgan, the torsion, and the Avalon fingerprints. The RDKit fingerprint still performs reasonably well with a KS₉₀ of 1.70, whereas values of 4.22 and 8.80 for the atom pair fingerprint and its hashed variant indicate poor performance of the model in this region.

In addition to the unconditional model, conditional distributions were investigated when a reference fingerprint was given. As each reference fingerprint will yield a different model, 100 compounds were randomly chosen as a reference and conditional models were derived and compared to empirical Tc distributions by comparing the reference compound to 100,000 randomly chosen compounds. The ranges of correspondences between empirical and modeled significance values are shown in Figure 2. The MACCS and Morgan fingerprints again showed the best conditional models, all of which were close to the ideal diagonal. For most reference compounds, the topological torsion fingerprint also yielded very good models; however, few outliers with large deviations were observed. This might be expected when reference fingerprints only contain very few features and approximations by normal distributions fail to yield accurate models.

Figure 2. Empirical versus modeled significance values.

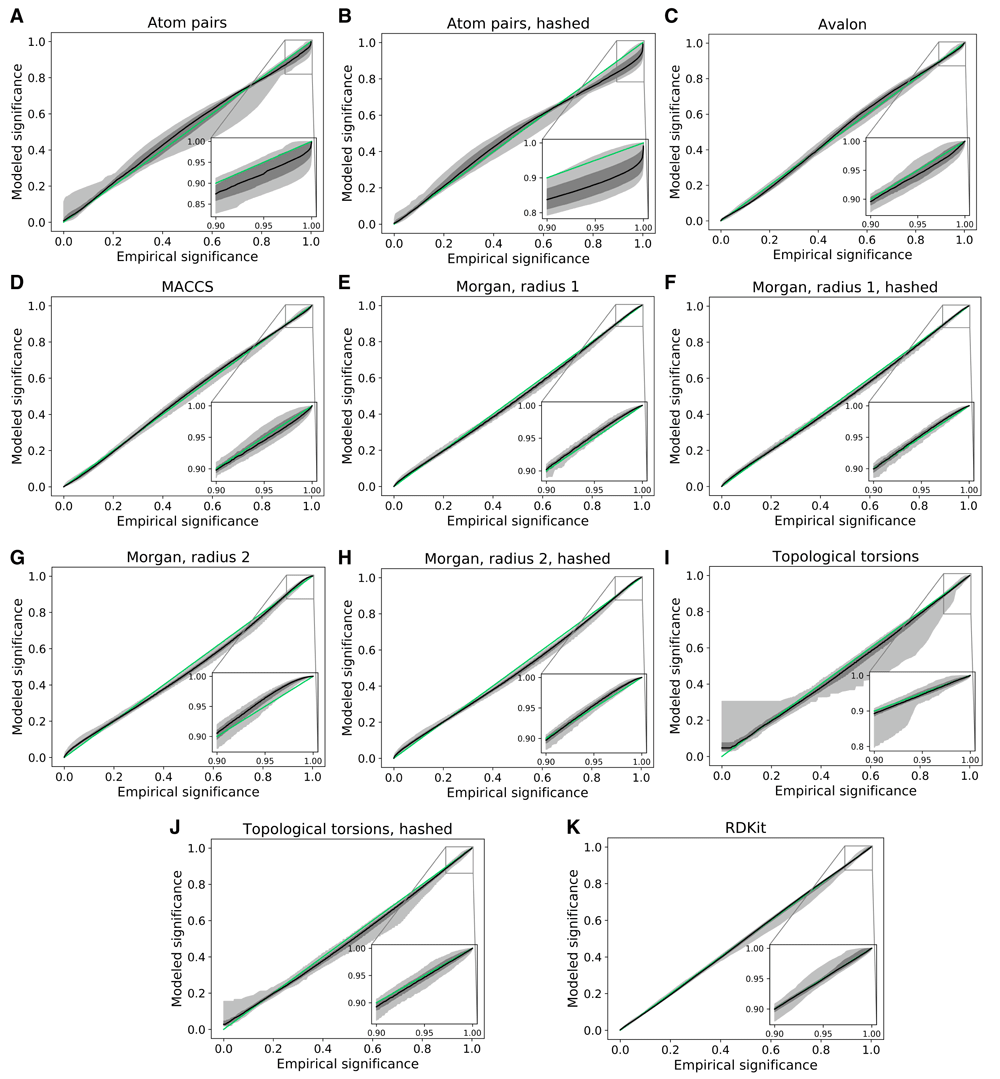
For the fingerprints in Table 1, each of the graphs (a) – (k) shows the variation of correspondences between empirical and modeled significance values of 100 conditional distributions obtained by selecting random reference compounds. Empirical distributions for each reference compound were determined from comparisons of 100,000 randomly chosen compounds. The black line indicates the median correspondence between empirical and modeled distribution. The dark gray area shows the interquartile range and the light gray area the range from the 5^th to the 95^th percentile. The green line is the diagonal corresponding to a perfectly matching model. The inserts highlight correspondences for significance values larger than 0.9.

The Python code used for data generation, data analysis, and generation of the figures is available in form of a Jupyter notebook in the github repository²⁷.

Conclusions

The tools provided make it possible to evaluate the significance of Tc values for a variety of fingerprints from RDKit. Users can generate distribution models for different fingerprints with respect to reference data sets. Accurate models are obtained for most RDKIT fingerprints including the popular MACCS and Morgan fingerprints. Based on these models, it can be assessed to what extent molecular similarity is accounted for by fingerprints of different design and to what extent similarity between compounds sharing the same activity is reflected by similarity scores calculated on the basis of different fingerprint representations. Furthermore, the conditional models can be used to predict the suitability of fingerprints for similarity searching and ligand-based virtual screening.

Data availability

Source data

The data sets used in this paper are freely available from ChEMBL: https://www.ebi.ac.uk/chembl/

Smiles structure representations were retrieved on 15 Jan 2020 from: ftp://ftp.ebi.ac.uk/pub/databases/chembl/ChEMBLdb/latest/chembl_25_chemreps.txt.gz

Software availability

RDKit

Our package depends on RDKit, which is freely available from https://www.rdkit.org

Source code is available from: https://github.com/vogt-m/ccbmlib

Archived source code at time of publication: https://doi.org/10.5281/zenodo.3634953²⁷

License: MIT

Faculty Opinions recommended

References

1. Willett P, Barnard JM, Downs GM: Chemical similarity searching. J Chem Inf Comp Sci. 1998; 38(6): 983–996. Publisher Full Text
2. Willett P: Similarity methods in chemoinformatics. Ann Rev Inf Sci Technol. 2009; 43(1): 1–117. Publisher Full Text
3. Maggiora GM, Shanmugasundaram V: Molecular similarity measures. In Chemoinformatics and computational chemical biology. Humana Press, Totowa, NJ. Methods Mol Biol. 2011; 672: 39–100. PubMed Abstract | Publisher Full Text
4. Maggiora G, Vogt M, Stumpfe D, et al.: Molecular similarity in medicinal chemistry: miniperspective. J Med Chem. 2014; 57(8): 3186–3204. PubMed Abstract | Publisher Full Text
5. Eckert H, Bajorath J: Molecular similarity analysis in virtual screening: foundations, limitations and novel approaches. Drug Discov Today. 2007; 12(5–6): 225–233. PubMed Abstract | Publisher Full Text
6. Stumpfe D, Bajorath J: Similarity searching. Wiley Interdiscip Rev Comput Mol Sci. 2011; 1(2): 260–282. Publisher Full Text
7. Willett P: Combination of similarity rankings using data fusion. J Chem Inf Model. 2013; 53(1): 1–10. PubMed Abstract | Publisher Full Text
8. Maggiora GM, Bajorath J: Chemical space networks: a powerful new paradigm for the description of chemical space. J Comput Aided Mol Des. 2014; 28(8): 795–802. PubMed Abstract | Publisher Full Text
9. Guha R: Exploring structure–activity data using the landscape paradigm. Wiley Interdiscip Rev Comput Mol Sci. 2012; 2(6): 829–841. PubMed Abstract | Publisher Full Text | Free Full Text
10. Rogers DJ, Tanimoto TT: A computer program for classifying plants. Science. 1960; 132(3434): 1115–1118. PubMed Abstract | Publisher Full Text
11. Jaccard P: The distribution of the flora in the alpine zone. New phytol. 1912; 11(2): 37–50. Publisher Full Text
12. Baldi P, Nasr R: When is chemical similarity significant? The statistical distribution of chemical similarity scores and its extreme values. J Chem Inf Model. 2010; 50(7): 1205–1222. PubMed Abstract | Publisher Full Text | Free Full Text
13. Vogt M, Bajorath J: Introduction of the conditional correlated Bernoulli model of similarity value distributions and its application to the prospective prediction of fingerprint search performance. J Chem Inf Model. 2011; 51(10): 2496–2506. PubMed Abstract | Publisher Full Text
14. Vogt M, Bajorath J: Modeling Tanimoto Similarity Value Distributions and Predicting Search Results. Mol Inform. 2017; 36(7): 1600131. PubMed Abstract | Publisher Full Text
15. RDKit: open-source cheminformatics software. (accessed Jan 27, 2020). Reference Source
16. Gaulton A, Hersey A, Nowotka M, et al.: The ChEMBL database in 2017. Nucleic Acids Res. 2017; 45(D1): D945–D954. PubMed Abstract | Publisher Full Text | Free Full Text
17. Carhart RE, Smith DH, Venkataraghavan R: Atom pairs as molecular features in structure-activity studies: definition and applications. J Chem Inf Comp Sci. 1985; 25(2): 64–73. Publisher Full Text
18. Gedeck P, Rohde B, Bartels C: QSAR--how good is it in practice? Comparison of descriptor sets on an unbiased cross section of corporate data sets. J Chem Inf Model. 2006; 46(5): 1924–1936. PubMed Abstract | Publisher Full Text
19. MACCS Structural Keys. Accelrys: San Diego, CA. 2011. Reference Source
20. Rogers D, Hahn M: Extended-connectivity fingerprints. J Chem Inf Model. 2010; 50(5): 742–54. PubMed Abstract | Publisher Full Text
21. Nilakantan R, Bauman N, Dixon JS, et al.: Topological torsion: a new molecular descriptor for SAR applications. Comparison with other descriptors. J Chem Inf Comp Sci. 1987; 27(2): 82–85. Publisher Full Text
22. Daylight Theory manual. Daylight Chemical Information Systems, Inc : Laguna Niguel, CA. (accessed Jan 27, 2020). Reference Source
23. Marsaglia G: Ratios of normal variables and ratios of sums of uniform variables. J Am Stat Assoc. 1965; 60(309): 193–204. Publisher Full Text
24. Hinkley DV: On the ratio of two correlated normal random variables. Biometrika. 1969; 56(3): 635–639. Publisher Full Text
25. de la Vega de León A, Lounkine E, Vogt M, et al.: Design of diverse and focused compound libraries. In: Tutorials in Chemoinformatics. John Wiley & Sons Ltd, Chichester, UK. 2017; 83–101. Publisher Full Text
26. Birnbaum ZW, Tingey FH: One-Sided Confidence Contours for Probability Distribution Functions. Ann Math Stat. 1951; 22(4): 592–596. Reference Source
27. Vogt M, Bajorath J: ccbmlib – a Python Package for Modeling Tanimoto Coefficient Distributions for Molecular Fingerprints (Version v1.0). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.3634953

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 10 Feb 2020

Author details Author details

¹ Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, NRW, 53115, Germany

Martin Vogt
Roles: Conceptualization, Data Curation, Formal Analysis, Methodology, Software, Writing – Original Draft Preparation

Jürgen Bajorath
Roles: Conceptualization, Methodology, Supervision, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 05 Mar 2020, 9:100

https://doi.org/10.12688/f1000research.22292.2

version 1

Published: 10 Feb 2020, 9:100

https://doi.org/10.12688/f1000research.22292.1

© 2020 Vogt M and Bajorath J. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Vogt M and Bajorath J. ccbmlib – a Python package for modeling Tanimoto similarity value distributions [version 1; peer review: 2 approved]. F1000Research 2020, 9(Chem Inf Sci):100 (https://doi.org/10.12688/f1000research.22292.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 1

VERSION 1

PUBLISHED 10 Feb 2020

Views

Reviewer Report 28 Feb 2020

David A. Cosgrove, CozChemix Limited, Macclesfield, UK

Approved

https://doi.org/10.5256/f1000research.24591.r59805

The authors report a method for analysing the occurrence of features in a set of fingerprints that have been generated from a reference collection of chemical structures. They use this analysis to generate models for assessing the statistical significance of the tanimoto coefficients for pairs of fingerprints in the set. Using the model, they can produce a plot of significance vs tanimoto coefficient (a CDF). In the paper, the accuracy of the model is assessed by comparing the curve so produced with those created by calculating the tanimoto coefficients for pairs of fingerprints from a large random sample of the set. The correspondence between the modelled and empirical distribution functions is high.

The paper is clearly laid out and relatively easy to read, if one takes the maths at face value. It is likely that it would be possible to reproduce their analysis from the information given. However, that is not strictly necessary from a practical standpoint as the authors have made the software they have developed for the analysis available as a Python module for anyone to download and use. They are to be commended for this action, which is still rare in the field of cheminformatics. It is likely to increase the impact of the paper considerably.

When I read a paper of this nature, a key question I pose myself is “how, if at all, will this help me with my work?” Here I fear the authors have been less successful. For example, there is an implementation in the RDKit toolkit of the Taylor-Buttina clustering method. This is a popular way of clustering fingerprints, and hence molecules, that is widely used for things like analysis of high-throughput screening results, organising the results from a virtual screen etc. A key input parameter to the algorithm is a threshold tanimoto coefficient – all fingerprints within a cluster are guaranteed to be within this similarity of the first fingerprint placed in the cluster. The success of this method for clustering depends very strongly on the value chosen for this threshold. Too high, and one obtains an unhelpfully large number of small clusters; too low, and the clusters will be large and contain molecules without apparent similarity. It would be very useful if there were a way of taking a successful threshold for one fingerprint type and using it to decide upon a similarly successful threshold for a different type. I feel as though this paper contains a way of doing this, but it is unclear to me quite how it would be achieved with the results presented. If the authors could add to the paper an example of how one would take a CDF for one fingerprint type and use it to translate a useful tanimoto coefficient threshold for it into an equally useful threshold for a different fingerprint type, that would, in my opinion, make the paper much more valuable.

Is the rationale for developing the new software tool clearly explained?

Partly
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Cheminformatics software development within the pharmaceutical industry.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response (F1000Research Advisory Board Member) 05 Mar 2020

Jürgen Bajorath, Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, 53115, Germany

05 Mar 2020

Author Response F1000Research Advisory Board Member

Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, ... Continue reading Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, a paragraph has been added to the manuscript explaining how modeled distributions can be used to identify corresponding Tanimoto coefficients (Tc values) for fingerprints of different design. In addition, a figure has been added displaying the relationship between MACCS Tc values and Tc values of other fingerprints. The software and Jupyter notebook have been updated accordingly.
Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, a paragraph has been added to the manuscript explaining how modeled distributions can be used to identify corresponding Tanimoto coefficients (Tc values) for fingerprints of different design. In addition, a figure has been added displaying the relationship between MACCS Tc values and Tc values of other fingerprints. The software and Jupyter notebook have been updated accordingly.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response (F1000Research Advisory Board Member) 05 Mar 2020

Jürgen Bajorath, Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, 53115, Germany

05 Mar 2020

Author Response F1000Research Advisory Board Member

Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, ... Continue reading Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, a paragraph has been added to the manuscript explaining how modeled distributions can be used to identify corresponding Tanimoto coefficients (Tc values) for fingerprints of different design. In addition, a figure has been added displaying the relationship between MACCS Tc values and Tc values of other fingerprints. The software and Jupyter notebook have been updated accordingly.
Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, a paragraph has been added to the manuscript explaining how modeled distributions can be used to identify corresponding Tanimoto coefficients (Tc values) for fingerprints of different design. In addition, a figure has been added displaying the relationship between MACCS Tc values and Tc values of other fingerprints. The software and Jupyter notebook have been updated accordingly.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 28 Feb 2020

Brian Goldman, Modeling & Informatics, Vertex Pharmaceuticals, Boston, MA, USA

Approved

https://doi.org/10.5256/f1000research.24591.r59806

The article ‘ccbmlib: a Python package for modeling Tanimoto similarity value distributions’, by Vogt and Bajorath is clearly written and concretely describes a method for determining the significance of tanimoto similarity scores. The statistical technique detailed in the paper outlines a mathematical method for converting tanimoto similarity scores from various binary molecular fingerprints into significance (p) values. Consequently, the method provides a way of normalizing similarity scores so that comparisons between results of searches utilizing different fingerprinting methods can be conducted easily. The paper also outlines a ‘conditional method’ that provides a technique for estimating the distributions of similarity scores for a given reference compound. This allows one to estimate how well a test compound would rank in a large-scale similarity search.

The explanations and mathematical equations in the paper are easy to follow. The graphs in the results section clearly support the findings of the study. I would recommend this paper to be indexed in its current form.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: machine learning for computational chemistry, statistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response (F1000Research Advisory Board Member) 05 Mar 2020

Jürgen Bajorath, Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, 53115, Germany

05 Mar 2020

Author Response F1000Research Advisory Board Member

Thank you for your instructive comments on the manuscript.
Competing Interests: No competing interests were disclosed.
Thank you for your instructive comments on the manuscript.
Thank you for your instructive comments on the manuscript.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response (F1000Research Advisory Board Member) 05 Mar 2020

Jürgen Bajorath, Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, 53115, Germany

05 Mar 2020

Author Response F1000Research Advisory Board Member

Thank you for your instructive comments on the manuscript.
Competing Interests: No competing interests were disclosed.
Thank you for your instructive comments on the manuscript.
Thank you for your instructive comments on the manuscript.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 10 Feb 2020

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 05 Mar 20
Version 1 10 Feb 20	read	read

Brian Goldman, Vertex Pharmaceuticals, Boston, USA
David A. Cosgrove, CozChemix Limited, Macclesfield, UK

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

21 Views

28 Feb 2020 | for Version 1

David A. Cosgrove, CozChemix Limited, Macclesfield, UK

21 Views Cite this report Responses(1)

Approved

Is the rationale for developing the new software tool clearly explained?

Partly
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Cheminformatics software development within the pharmaceutical industry.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response F1000Research Advisory Board Member

05 Mar 2020

Jürgen Bajorath, Department of Life Science Informatics, B-IT, University of Bonn, Endenicher Allee 19c, Bonn, 53115, Germany

Thank you for your comments and your suggestion. Indeed, a potential application of the methodology is establishing correspondences between Tc values of different fingerprints according to their statistical significance. Therefore, a paragraph has been added to the manuscript explaining how modeled distributions can be used to identify corresponding Tanimoto coefficients (Tc values) for fingerprints of different design. In addition, a figure has been added displaying the relationship between MACCS Tc values and Tc values of other fingerprints. The software and Jupyter notebook have been updated accordingly.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

20 Views

28 Feb 2020 | for Version 1

Brian Goldman, Modeling & Informatics, Vertex Pharmaceuticals, Boston, MA, USA

20 Views Cite this report Responses(1)

Approved

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

machine learning for computational chemistry, statistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Willett P, Barnard JM, Downs GM: Chemical similarity searching. J Chem Inf Comp Sci. 1998; 38(6): 983–996. Publisher Full Text

[2] 2. Willett P: Similarity methods in chemoinformatics. Ann Rev Inf Sci Technol. 2009; 43(1): 1–117. Publisher Full Text

[3] 3. Maggiora GM, Shanmugasundaram V: Molecular similarity measures. In Chemoinformatics and computational chemical biology. Humana Press, Totowa, NJ. Methods Mol Biol. 2011; 672: 39–100. PubMed Abstract | Publisher Full Text

[4] 4. Maggiora G, Vogt M, Stumpfe D, et al.: Molecular similarity in medicinal chemistry: miniperspective. J Med Chem. 2014; 57(8): 3186–3204. PubMed Abstract | Publisher Full Text

[5] 5. Eckert H, Bajorath J: Molecular similarity analysis in virtual screening: foundations, limitations and novel approaches. Drug Discov Today. 2007; 12(5–6): 225–233. PubMed Abstract | Publisher Full Text

[6] 6. Stumpfe D, Bajorath J: Similarity searching. Wiley Interdiscip Rev Comput Mol Sci. 2011; 1(2): 260–282. Publisher Full Text

[7] 7. Willett P: Combination of similarity rankings using data fusion. J Chem Inf Model. 2013; 53(1): 1–10. PubMed Abstract | Publisher Full Text

[8] 8. Maggiora GM, Bajorath J: Chemical space networks: a powerful new paradigm for the description of chemical space. J Comput Aided Mol Des. 2014; 28(8): 795–802. PubMed Abstract | Publisher Full Text

[9] 9. Guha R: Exploring structure–activity data using the landscape paradigm. Wiley Interdiscip Rev Comput Mol Sci. 2012; 2(6): 829–841. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Rogers DJ, Tanimoto TT: A computer program for classifying plants. Science. 1960; 132(3434): 1115–1118. PubMed Abstract | Publisher Full Text

[11] 11. Jaccard P: The distribution of the flora in the alpine zone. New phytol. 1912; 11(2): 37–50. Publisher Full Text

[12] 12. Baldi P, Nasr R: When is chemical similarity significant? The statistical distribution of chemical similarity scores and its extreme values. J Chem Inf Model. 2010; 50(7): 1205–1222. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Vogt M, Bajorath J: Introduction of the conditional correlated Bernoulli model of similarity value distributions and its application to the prospective prediction of fingerprint search performance. J Chem Inf Model. 2011; 51(10): 2496–2506. PubMed Abstract | Publisher Full Text

[14] 14. Vogt M, Bajorath J: Modeling Tanimoto Similarity Value Distributions and Predicting Search Results. Mol Inform. 2017; 36(7): 1600131. PubMed Abstract | Publisher Full Text

[15] 15. RDKit: open-source cheminformatics software. (accessed Jan 27, 2020). Reference Source

[16] 16. Gaulton A, Hersey A, Nowotka M, et al.: The ChEMBL database in 2017. Nucleic Acids Res. 2017; 45(D1): D945–D954. PubMed Abstract | Publisher Full Text | Free Full Text

[17] 17. Carhart RE, Smith DH, Venkataraghavan R: Atom pairs as molecular features in structure-activity studies: definition and applications. J Chem Inf Comp Sci. 1985; 25(2): 64–73. Publisher Full Text

[18] 18. Gedeck P, Rohde B, Bartels C: QSAR--how good is it in practice? Comparison of descriptor sets on an unbiased cross section of corporate data sets. J Chem Inf Model. 2006; 46(5): 1924–1936. PubMed Abstract | Publisher Full Text

[19] 19. MACCS Structural Keys. Accelrys: San Diego, CA. 2011. Reference Source

[20] 20. Rogers D, Hahn M: Extended-connectivity fingerprints. J Chem Inf Model. 2010; 50(5): 742–54. PubMed Abstract | Publisher Full Text

[21] 21. Nilakantan R, Bauman N, Dixon JS, et al.: Topological torsion: a new molecular descriptor for SAR applications. Comparison with other descriptors. J Chem Inf Comp Sci. 1987; 27(2): 82–85. Publisher Full Text

[22] 22. Daylight Theory manual. Daylight Chemical Information Systems, Inc : Laguna Niguel, CA. (accessed Jan 27, 2020). Reference Source

[23] 23. Marsaglia G: Ratios of normal variables and ratios of sums of uniform variables. J Am Stat Assoc. 1965; 60(309): 193–204. Publisher Full Text

[24] 24. Hinkley DV: On the ratio of two correlated normal random variables. Biometrika. 1969; 56(3): 635–639. Publisher Full Text

[25] 25. de la Vega de León A, Lounkine E, Vogt M, et al.: Design of diverse and focused compound libraries. In: Tutorials in Chemoinformatics. John Wiley & Sons Ltd, Chichester, UK. 2017; 83–101. Publisher Full Text

[26] 26. Birnbaum ZW, Tingey FH: One-Sided Confidence Contours for Probability Distribution Functions. Ann Math Stat. 1951; 22(4): 592–596. Reference Source

[27] 27. Vogt M, Bajorath J: ccbmlib – a Python Package for Modeling Tanimoto Coefficient Distributions for Molecular Fingerprints (Version v1.0). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.3634953

ccbmlib – a Python package for modeling Tanimoto similarity value distributions

Abstract

Keywords

Introduction

Methods

Fingerprint representations

Table 1. Fingerprints available in RDKit.

Fingerprint similarity

Modeling similarity value distributions

Modeling conditional value distributions

Sparse fingerprints

Data sets

Implementation and operation

Results and discussion

Figure 1. Empirical and modeled cumulative distribution functions.

Table 2. Kolmogorov-Smirnov statistics.

Figure 2. Empirical versus modeled significance values.

Conclusions

Data availability

Source data

Software availability

RDKit

ccbmlib

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated