Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights

Romain D. Cazé; Marcel Stimberg

doi:10.12688/f1000research.26486.3

Home Browse Neurons with dendrites can perform linearly separable computations...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Revised

Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights

[version 3; peer review: 3 approved]

Previously titled: Dendritic neurons can perform linearly separable computations with low resolution synaptic weights

Romain D. Cazé ¹, Marcel Stimberg²

PUBLISHED 18 Apr 2021

Author details Author details

¹ IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France
² Institut de la vision, CNRS, INSERM, Paris, 75012, France

Romain D. Cazé
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Project Administration, Resources, Software, Validation, Visualization, Writing – Original Draft Preparation

Marcel Stimberg
Roles: Funding Acquisition, Investigation, Methodology, Software, Validation, Visualization, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the INCF gateway.

Abstract

In theory, neurons modelled as single layer perceptrons can implement all linearly separable computations. In practice, however, these computations may require arbitrarily precise synaptic weights. This is a strong constraint since both biological neurons and their artificial counterparts have to cope with limited precision. Here, we explore how non-linear processing in dendrites helps overcome this constraint. We start by finding a class of computations which requires increasing precision with the number of inputs in a perceptron and show that it can be implemented without this constraint in a neuron with sub-linear dendritic subunits. Then, we complement this analytical study by a simulation of a biophysical neuron model with two passive dendrites and a soma, and show that it can implement this computation. This work demonstrates a new role of dendrites in neural computation: by distributing the computation across independent subunits, the same computation can be performed more efficiently with less precise tuning of the synaptic weights. This work not only offers new insight into the importance of dendrites for biological neurons, but also paves the way for new, more efficient architectures of artificial neuromorphic chips.

Keywords

Dendrites, computation, linearly separable, implementation

Corresponding author: Romain D. Cazé

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by the following grants: LabEx LIFESENSES (ANR-10-LABX-65) and IHU FOReSIGHT (ANR-18-IAHU-01).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Cazé RD and Stimberg M. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Cazé RD and Stimberg M. Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights [version 3; peer review: 3 approved]. F1000Research 2021, 9:1174 (https://doi.org/10.12688/f1000research.26486.3) First published: 28 Sep 2020, 9:1174 (https://doi.org/10.12688/f1000research.26486.1) Latest published: 18 Apr 2021, 9:1174 (https://doi.org/10.12688/f1000research.26486.3)

Revised Amendments from Version 2

We reinforced the discussion and explicit what we meant using an example: for a linearly separable computation a TLU needs at least a thousand binary synapses while a few binary synapses suffice for a STLU. We also clarified Fig.4 and Fig.5, and corrected some minor typos.

See the authors' detailed response to the review by Sacha van Albada
See the authors' detailed response to the review by Alexandra Tzilivaki and Panayiota Poirazi
See the authors' detailed response to the review by Fleur Zeldenrust

Introduction

In theoretical studies, scientists typically represent neurons as linear threshold units (LTU; summing up the weighted inputs and comparing the sum to a threshold)¹. Multiple decades ago, theoreticians exactly delimited the computational capacities of LTUs, also known as perceptrons². LTUs cannot implement computations like the exclusive or (XOR), but they can implement all possible linearly separable computations and a sufficiently large network of LTUs can approximate all possible computations³.

Research in computer science investigated the synaptic weight resolution required to implement linearly separable computations^4,5. Hastad et al. studied a computation implementable by an LTU only if its synaptic weight resolution grows exponentially with the number of inputs. We consider, similarly to these studies, the needed resources as the minimal size of integer-valued weights necessary to implement a set of linearly separable computations.

Requiring a high synaptic resolution has important consequences. In the nervous system, neurons would need to maintain a large number of synapses or synapses with a large number of stable states. For the same reason, neuromorphic chips based on LTUs have to dedicate a large amount of resources to synapses⁶. We demonstrate here that dendrites might be a way to cope with this challenge.

Dendrites are the receptive elements of neurons where most of the synapses lie. They turn neurons into a multilayer network^7,8 because of their non-linear properties^9,10. These non-linearities enable neurons to perform linearly inseparable computations like the XOR or the feature binding problem^11,12. The non-linear integration also appears to be tuned for efficient integration of in vivo presynaptic activity¹³.

In this study, we investigate whether dendrites can also decrease the synaptic resolution necessary to implement linearly separable computations. We address this question by looking at all the computations of three input variables implementable by an LTU with positive synaptic weights. We then extend the definition of one of these computations to an arbitrarily high number of inputs. Finally, we implement this computation in a biophysical neuron model with two passive dendrites using fewer synapses than an LTU.

This work proposes a new role for dendrites in the nervous system, but also paves the way for a new generation of more cost-efficient artificial neural networks and neuromorphic chips composed of neurons with dendrites.

Methods

Biophysical neuron model

We performed simulations in a spatially extended neuron model, consisting of a spherical soma (diameter 10 µm) and two cylindrical dendrites (length 400 µm and diameter 0.4 µm). The two dendrites are each divided into four compartments and connect to the soma at one extremity.

In contrast to a point-neuron model, each compartment has a distinct membrane potential.

The membrane potential dynamics of the somatic compartment follows the Hodgkin-Huxley formalism with:

C_{m} \frac{d V_{soma}}{d t} = g_{L} (V - E_{L}) + {\bar{g}}_{K} n^{4} (V - E_{K}) + {\bar{g}}_{N a} m^{3} h (V - E_{N a}) + I_{a} + I_{s} (1)

The dendritic compartments only contain passive currents:

C_{m} \frac{d V_{dend}}{d t} = g_{L} (V - E_{L}) + I_{a} + I_{s} (2)

Here, V_somaand V_dendare the respective membrane potentials, C_m = 1µFcm⁻² is the membrane capacitance, g_L, $\bar{g}$ _K, and $\bar{g}$ _Na stand for the leak, the maximum potassium and sodium conductances respectively, and E_L, E_K, and E_Na stand for the corresponding reversal potentials. The currents I_a represent the axial currents due to the membrane potential difference between connected compartments. The synaptic current I_s arises from a synapse placed at the respective compartment. It is described by

I_{s} = g_{s} (E_{s} - V) (3)

with E_s being the synaptic reversal potential and g_s the synaptic conductance. This conductance jumps up instantaneously for each incoming spike and decays exponentially with time constant τ_s = 1 ms otherwise:

\frac{d g_{s}}{d t} = - \frac{g_{s}}{τ_{s}} (4)

The dynamics of the gating variables n, m, and h are identical to 14, except for shifting the membrane potential relative to V_T = –50 mV instead of the cell’s resting potential. The equations are omitted here for brevity. The parameter values are summarized in Table 1. Note that due to the absence of sodium and potassium channels in the dendrites, the dendrites are passive and cannot generate action potentials.

Table 1. Parameter values used in the biophysical model.

Equilibrium potentials (in mV)		Conductances (in mS/cm²)
E_L	−65	g_L	10
E_Na	50	$\bar{g}$ _Na	100
E_K	−90	$\bar{g}$ _K	30
E_s	0

All simulations were performed with Brian 2¹⁵. The code is available at http://doi.org/10.5281/zenodo.4315011¹⁶. It allows for reproducing the results presented in Figure 4, Figure 5 and Figure 6. To demonstrate that the details of the neuron model do not matter for the results presented here, the provided code can also be run with a simpler leaky integrate-and-fire model.

Elementary neuron model and Boolean functions

As a reminder, we first define Boolean functions:

Definition 1. A Boolean function of n variables is a function on {0, 1}ⁿ into {0, 1}, where n is a positive integer.

Note that we use the terms function and computation interchangeably.

A special class of Boolean functions, which are of particular relevance for neurons, are linearly separable computations:

Definition 2. f is a linearly separable computation of n variables if and only if there exists at least one vector w ∈ ℝⁿ and a threshold Θ ∈ ℝ such that:

f (X) = {\begin{matrix} 1 & i f w \cdot X \geq Θ \\ 0 & o t h e r w i s e \end{matrix}

where X ∈ {0, 1}ⁿ is the vector notation for the Boolean input variables.

Binary neurons are one of the simplest possible neuron models and closely related to the functions described above: their inputs are binary variables, representing the activity of their input pathways, and their output is a single binary variable, representing whether the neuron is active or not. The standard model is a linear threshold unit (LTU), defined as follows:

Definition 3. An LTU has a set of m weights w_i ∈ 𝒲 and a threshold Θ ∈ 𝒯so that:

f (X) = {\begin{matrix} 1 & i f \sum_{i = 1}^{m} w_{i} X_{i} \geq Θ \\ 0 & o t h e r w i s e \end{matrix}

where X = (X₁, . . . , X_m) are the binary inputs to the neuron, and 𝒲 and 𝒯 are the possible values for synaptic weights and the threshold, respectively.

This definition is virtually identical to Definition 2, however, w_i and Θ are no longer arbitrary real values, but chosen from a finite set of numbers depending on the specific implementation and noise at which these value can be stabilised. It follows that a neuron may not be able to implement all linearly separable functions. For instance, a neuron with non-negative weights can only perform positive linearly separable computations:

Definition 4. A threshold function f is positive if and only if f (X) ≥ f (Z) ∀(X , Z) ∈ {0, 1}ⁿ such that X ≥ Z (meaning that ∀i: x_i ≥ z_i).

To account for saturation occurring in dendrites, we introduce the sub-linear threshold unit (SLTU):

Definition 5. An SLTU with d dendrites and n inputs has a set of d × n weights w_i_,j ∈ {0, 1} with n w_isuch that $\sum_{j = 1}^{d} w_{i, j} = w_{i}$ and a threshold Θ ∈ 𝒯, such that:

f (X) = {\begin{matrix} 1 & i f \sum_{i = 1}^{d} E (\sum_{j = 1}^{n} w_{i, j} X_{i, j}) \geq Θ \\ 0 & otherwise \end{matrix}

with

E (Y) = {\begin{matrix} 1 & i f Y \geq 1 \\ Y & o t h e r w i s e \end{matrix}

The function E accounts for dendritic saturation; because we work with binary weights its value is either 0 or 1.

Such a neuron model can implement all positive Boolean computations (see Definition 4) given a sufficient number of dendrites and synapses¹¹.

We used integer-valued and non-negative parameters both for the LTU and the SLTU without loss of generality. It allows us to exactly determine the minimal resources necessary to implement a given computation.

Results

Implementation of computations with three input variables

We begin by listing all computations of n = 3 inputs that are implementable by an LTU (i.e., positive threshold functions; Table 2). These computations can be divided in five classes, and one can obtain all computations from a class by swapping the input labels. The OR, AND/OR, and AND can be implemented with equal synaptic weights. In contrast, the remaining classes require heterogeneous synaptic weights. We call these classes the Dominant AND (D-AND) and the Dominant OR (D-OR): to implement these computations, an LTU needs to have one synaptic weight that is twice as big as the others (see Figure 1).

Table 2. The five classes of positive threshold functions for n = 3 inputs with their associated truth tables.

We have assigned a name to each class for easier reference.

Inputs	OR	AND/OR	AND	D-OR	D-AND
000	0	0	0	0	0
001	1	0	0	0	0
010	1	0	0	0	0
011	1	1	0	1	0
100	1	0	0	1	0
101	1	1	0	1	1
110	1	1	0	1	1
111	1	1	1	1	1

The D-AND computation gets its name from the fact that it requires the activation of a dominant (D) input AND the activation of another input. The D-OR is the Boolean dual of the D-AND, i.e. obtained by replacing AND operations by OR, and vice versa. In this computation, activation of the dominant input OR of the two other inputs together triggers an output. Both computations have a “dominant input” – an input that is sufficient to make the output true (D-OR), respectively necessary to make the output true (D-AND). There is nothing comparable in the other three computations, which treat all inputs identically. In the present paper, we always chose X₁as the dominant input, but we could have picked X₂ or X₃.

Figure 1. Minimal implementation of the Dominant AND computation (D-AND) and its dual by a linear threshold unit (LTU).

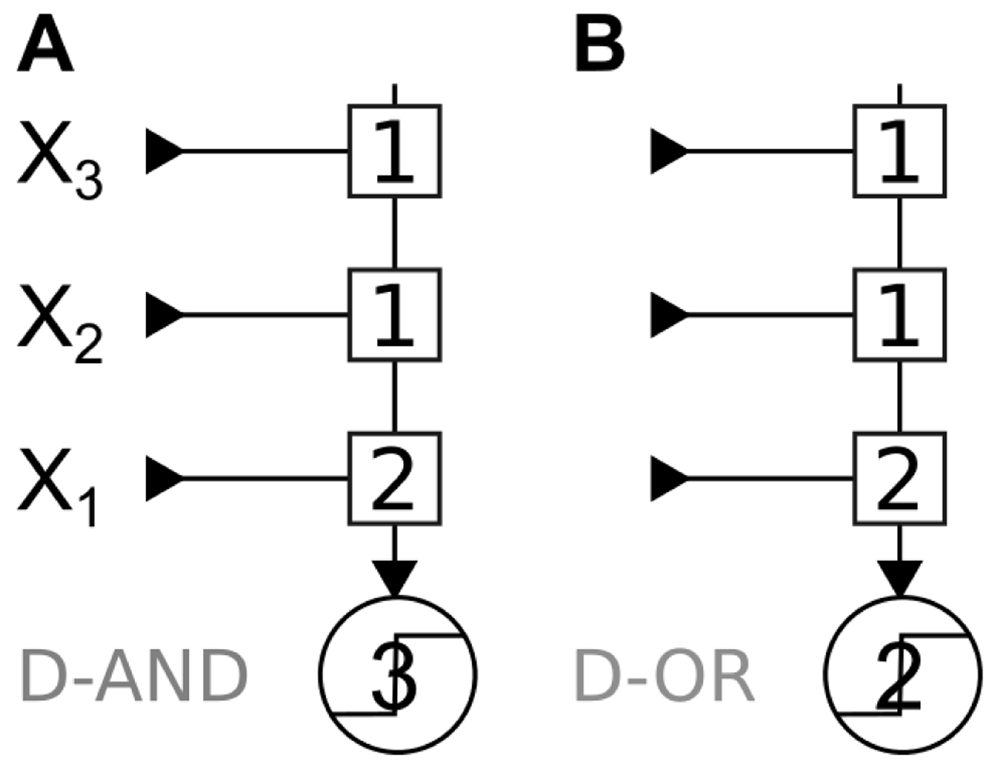
Implementations of the D-AND where X₁is the dominant input. Squares represent synapses with their synaptic weight, and circles stand for transfer functions. Here, the transfer functions are threshold functions with the given value as their threshold. A: Implementation of the D-AND, note that X₁has twice the synaptic weight compared to the others. B: Implementation of the D-OR, note that we keep the same synaptic architecture and we only change the threshold of the transfer function.

An LTU (Figure 1) implements D-AND and D-OR by making use of synaptic strength to distinguish between the dominant and non-dominant inputs. We employed synaptic weights with integer values to reflect their finite precision. Even if synaptic weights can take real values, a finite precision means a finite number of values, which again can be represented by an integer value. The weight and threshold values to implement a function are obviously not unique. For example, we could multiply all the weights by 2 and set the threshold to 6 (D-AND), or 4 (D-OR) and obtain the same results. Here, we always use the lowest possible integer values for synaptic weights, and the corresponding lowest possible threshold.

Next, we wanted to implement the D-AND and D-OR computation in threshold units with non-linear dendritic sub-units, as an abstraction of neurons with dendrites⁷.

We consider two types of non-linearities: a threshold function to model supra-linear summation; and a saturating function to model sub-linear summation (SLTU; see Methods). Both types of summation have been observed in dendrites. Dendritic spikes are a well-known example of supra-linear summation¹², while sub-linear summation can be observed in completely passive dendrites due to a reduced driving force⁹.

On the one hand, Figure 2 (top) shows that a neuron with supra-linear dendrites implements the D-OR using space whereas the sub-linear implementation uses strength. On the other hand, Figure 2 (bottom) shows that a neuron with supra-linear dendrites implements the D-AND using strength whereas the sub-linear implementation uses space.

Figure 2. Minimal implementation of the Dominant AND computation (D-AND) and its dual (D-OR) by a neuron with dendrites.

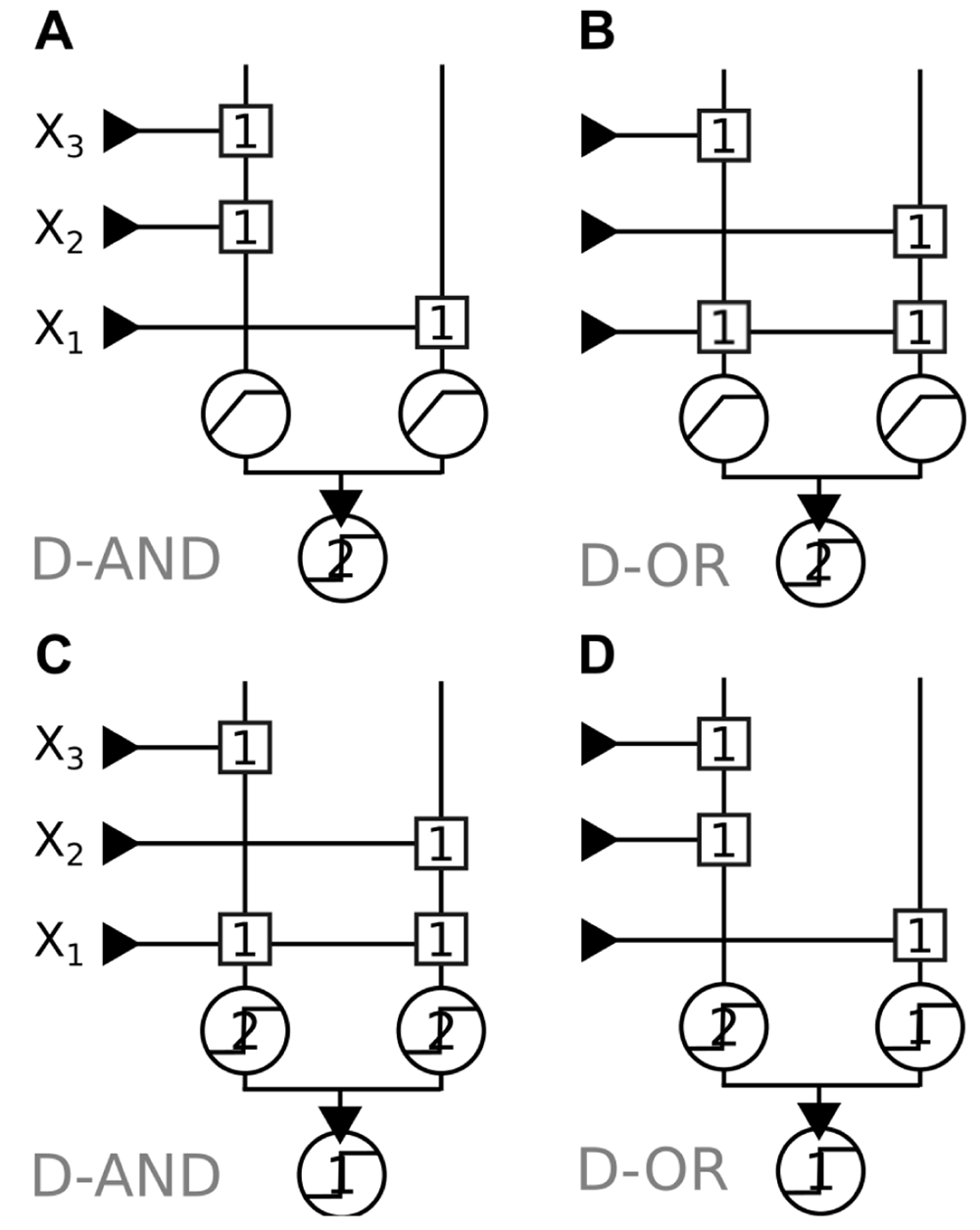
Squares represent synapses and circles represent transfer functions with their respective threshold/saturation values. Note that the final transfer functions (“somatic integration”) are always threshold units, whereas the transfer functions of the sub-units (“dendrites”) are threshold functions for supra-linear summation, and saturating functions (corresponding to the E function defined in Definition 5) for strictly sub-linear summation. A: D-AND implementation using sub-linear summation where X₁targets only one dendrite. B: D-OR implementation, in this case X₁targets two sub-linear dendrites. C: D-AND implementation using supra-linear summation, where X₁targets two dendrites. D: D-OR implementation, X₁ in this case targets only one dendrite.

In both cases, all synapses are of identical strength. However, note that in the supra-linear implementation of the D-AND in Figure 2C the X₁ input connects to both dendrites. Therefore, if we define an input’s synaptic weight as the total effect it has in the final summation stage (analogous to depolarisation measured in the soma of a neuron), we have to consider the weight of X₁as twice as high as the other inputs. This makes this implementation “as bad as” the implementation in an LTU (Figure 1A): the dominance of X₁is expressed by a stronger weight.

This starkly contrasts with the sub-linear implementation of the D-AND (Figure 2D), where all synaptic weights are identical. The placement of X₁’s synapse causes its dominance: while X₂and X₃share a dendrite, X₁’s synapse lies alone on a dendrite. This implementation uses space. We focus on sub-linear summation and the D-AND for the rest of the study.

Implementing the D-AND for an arbitrary number of input variables

In the previous section, we have limited our analysis to computations with three input variables. We will now extend the definition of the D-AND to an arbitrary number of input variables. As in the three-variables case, we will consider one input to be the dominant input (assumed to be X₁, without loss of generality). This input has to be activated together with at least one of the non-dominant inputs. Formally, we therefore define f_n(X) as follows:

f_{n} (X) = X_{1} \land (V_{i = 2}^{n} X_{i}) (5)

where X is the n-dimensional input vector with elements X₁... X_n.

We can implement this computation in an LTU (Figure 3A), as well as in an SLTU (Figure 3B)

In the LTU implementation (Figure 3A), the D-AND of n variables requires that an input has a synaptic weight at least n − 1 times bigger than the other inputs, and the threshold has to grow accordingly.

Figure 3. Extending the D-AND implementation to n inputs.

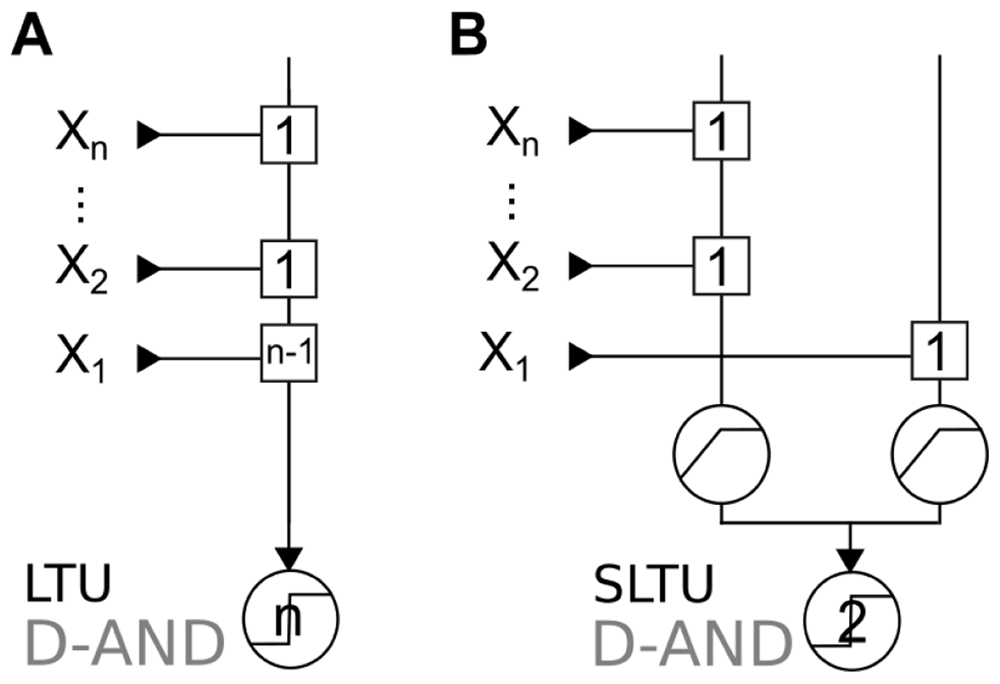
Synaptic weights are in squares, and transfer functions are in circles. A: Minimal D-AND implementation in an LTU. Note that this implementation requires a synaptic weight that is n − 1 times bigger than the smallest weight. B: Implementation in an SLTU with sub-linear summation (see Definition 5).

We can summarise these observations in a proposition.

Proposition 1. To implement the D-AND, an LTU requires that an input has a synaptic weight n − 1 times bigger than the smallest synaptic weight.

Proof. The LTU must stay silent when X₁ is not active, even if X₂, X₃, . . . , X_n are active. Therefore w₂ + w₃ + ... + w_n < Θ, thus Θ must be at least n × w_min with w_min the smallest synaptic weight.

Conversely, the output should be active as soon as X₁ is co-active with any other input X_j (for j > 1). So w₁ + w_min ≥ Θ, this means w₁ + w_min ≥ n × w_min, thus w₁ ≥ w_min(n − 1).

In contrast, Figure 3B provides a constructive proof that an SLTU can implement the D-AND with equal synaptic weights. In this implementation, the distinguishing feature of the dominant input is that it targets the second dendrite; synaptic weights and the threshold do not have to change with the number of inputs. If one only measured the response to single inputs at the “soma” (last stage of summation), the dominant input would be indistinguishable from the other inputs, despite its dramatically different importance.

We will see next how these insights transfer to a more realistic biophysical model.

Implementation of the D-AND in a biophysical model

Figure 4A presents a biophysical model of a single neuron implementing the D-AND computation with three groups of synapses. All the synapses, taken individually, produced the exact same depolarisation at the soma because we place them at the same distance (350 µm) and give them the same maximal conductance (20 nS).

Figure 4. A biophysical model sensitive to synapses’ spatial distribution.

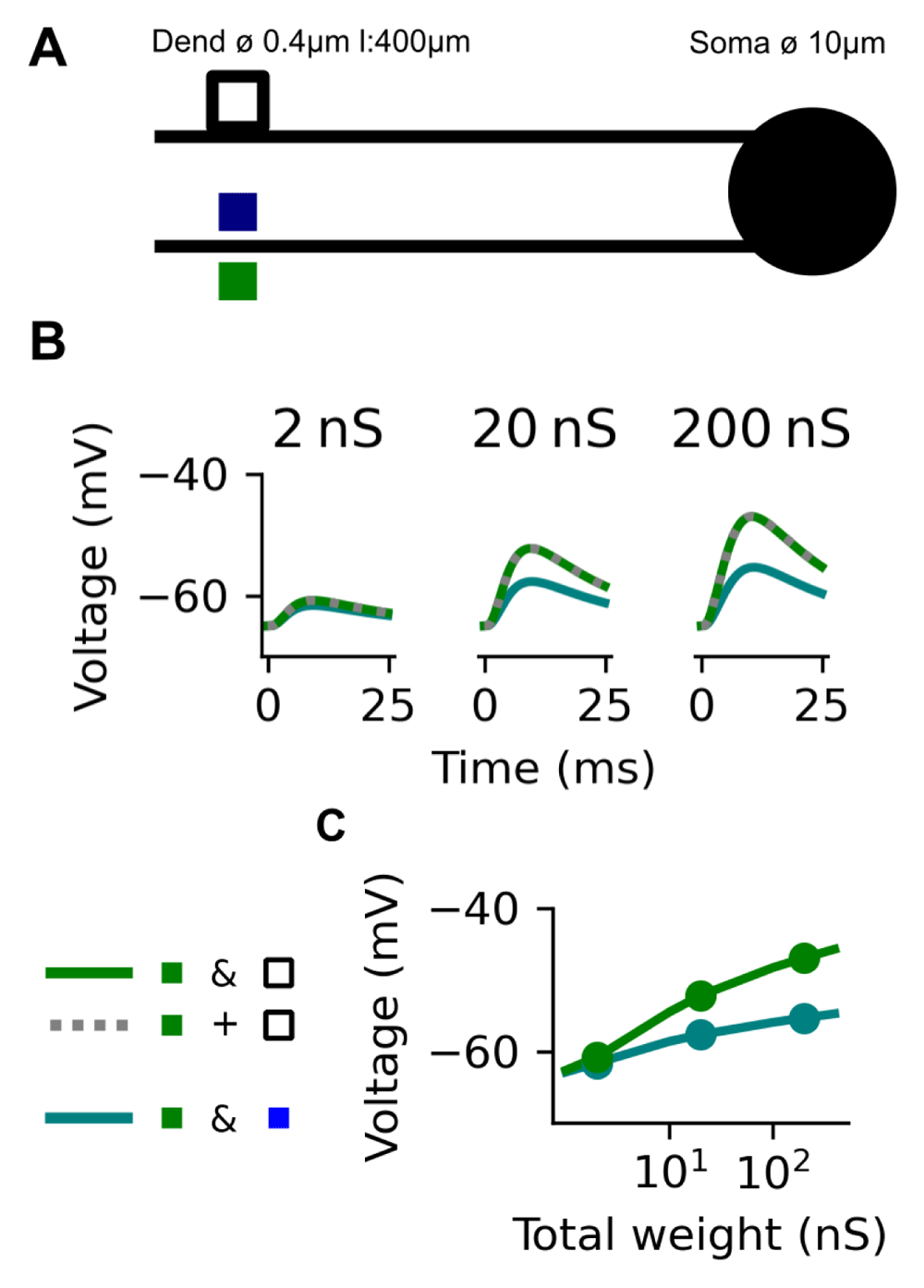
A: A biophysical model with two dendrites and a soma (lines: dendrites, circle: soma). Coloured squares depict synapses. The model has three equivalent groups of synapses (black edges/blue/green). B: Somatic membrane voltage traced in 3 scenarios: either two groups of synapses activated simultaneously (& symbol) or we linearly added the response from two synaptic groups (+ symbol) note that the green and dotted grey line overlay C: Maximal membrane voltage at the soma depending on the total synaptic weight for either clustered (aquamarine) or dispersed (green) stimulation. We omitted the grey dotted line here as it overlays with the green.

We first look at the sub-threshold behaviour by disabling the sodium channels in the soma ( $g_{N a}^{m a x}$ = 0). Figure 4B plots the somatic voltage response at distinct locations in response to either clustered (black) or dispersed (aquamarine) synaptic activation. Despite activating the same number of synapses in both cases, and despite them all having the same strength, the depolarisation is markedly different. When we disperse active synapses, EPSPs sum linearly (same as dotted gray line) whereas when we cluster active synapses summation becomes sub-linear. This difference is robust with respect to the specific values of the synaptic weights. As shown in Figure 4C, the dispersed activation always exceeds the clustered activation, for the same total synaptic weight. This difference remains even for a total weight bigger for the clustered than the dispersed case. For example, a clustered activation with a total weight of 100 nS leads to a maximum membrane potential of only −54mV in the soma, whereas a dispersed activation with a mere total weight of 10 nS leads to a maximal membrane potential of −52.5mV.

We can explain this observation by considering the synaptic driving force¹⁷. The synaptic current induced by the activation of the synapse depends on the distance between the membrane potential and the synapses’ reversal potential; when several inputs drive the membrane potential closer to the reversal potential (here 0mV), this driving force diminishes. The combined effect of multiple synaptic inputs is therefore smaller than what is expected from summing the individual effects. In other words, the dendrite performs sub-linear summation.

This means that even if we have a complete synaptic democracy¹⁸ (all synapses have the same impact on the soma when taken individually), the relative placement of the synapses strongly influences the somatic response.

Based on the sub-threshold behaviour presented above, we will now show that we can implement the D-AND in a spiking neuron model. It is crucial to look at the supra-threshold behaviour as it is how the neuron communicates with the rest of the network. Moreover, backpropagated action potentials might undermine the dendritic non-linearity disrupting the implementation¹⁹.

We can interpret Boolean inputs and outputs in different ways when we apply them to a biophysical spiking neuron model. Here, we will consider two interpretations. Firstly, we can think of an active input as corresponding to a continuous stimulation where the individual spikes arrive at random times, and of an active output as some spiking activity of the neuron (“rate interpretation”). Alternatively, we can think of active inputs as coincidentally arriving spikes within a certain time window, and accordingly of an active output as a single spike emitted in response (“spike interpretation”). We present the model implementing the rate interpretation in Figure 5. We introduced this model earlier (Figure 4), except that it now has active sodium channels in the soma ( $g_{N a}^{m a x}$ = 650mS cm^–2). Each of its inputs (colours corresponding to the colours in Figure 4) activates in 25 randomly chosen time-bins of 1 ms to simulate a 100 Hz spike train over 250 ms.

Figure 5. A biophysical model implementing the Dominant AND (rate interpretation).

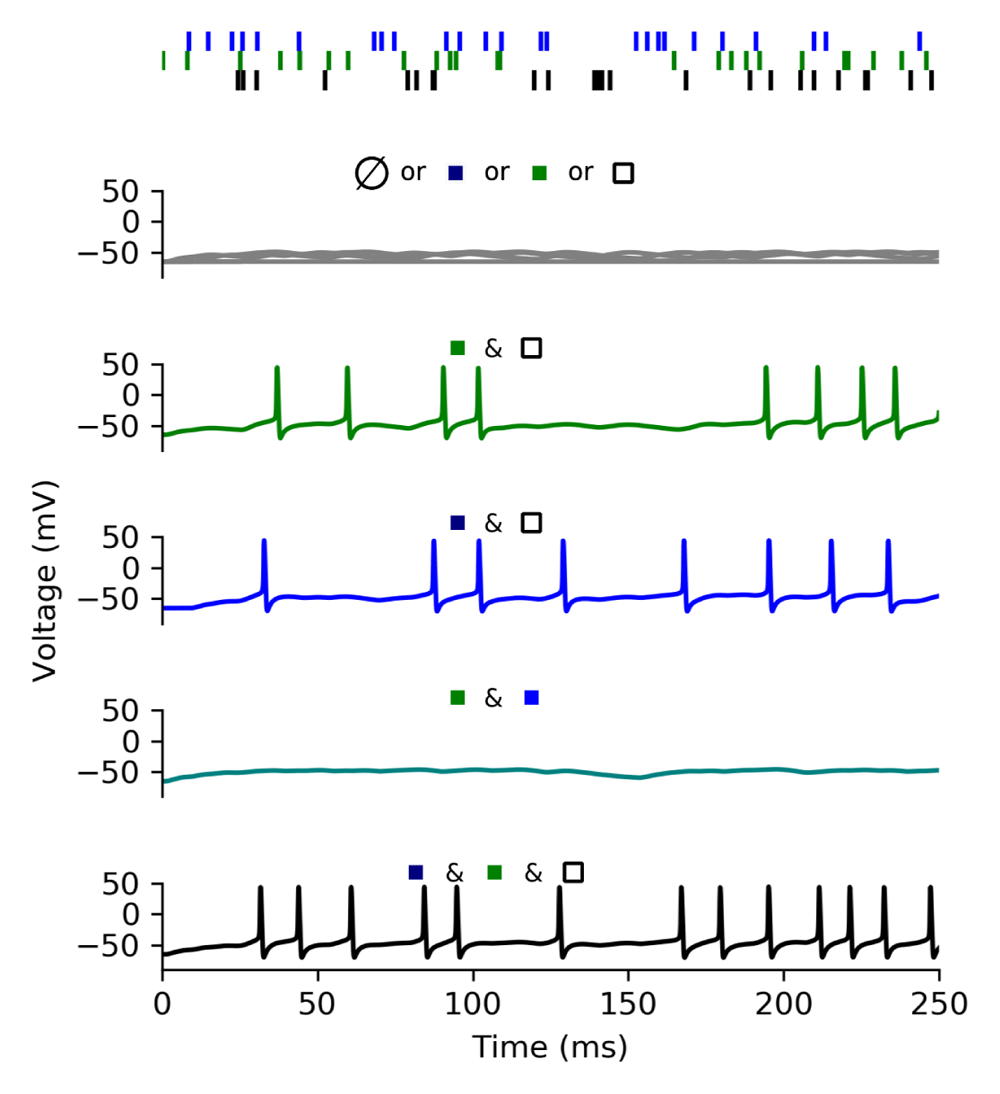
We show in this figure how the model presented in the previous figure responds in 8 different cases. X_i = 1 corresponds to a presynaptic neuron firing at 100Hz and the 8 cases correspond to the truth table. Top: activity of the three input synapses, the two first synapses impinge on the same dendrite while the black one impinges on another. Bottom: Eight somatic membrane responses depending on the active inputs. (gray: no synapse/only black/green/blue, green: black + green, blue: black + blue, aquamarine: green + blue, black: all inputs active). The difference between the aquamarine line (green and blue inputs) and the green and blue lines (black input and either green or blue input) is due to the sub-linear summation in the dendrite. With linear summation these three responses would have been identical -either all firing or not.

The Figure 5 displays, from top to bottom, the model’s responses in five different situations:

A single input activates, in this case the neuron remains silent. We obtain the same outcome whatever the chosen input.
Two groups of dispersed inputs activate (black + green or black + blue), in these two scenarios the neuron fires.
The two groups of clustered inputs (green + blue) activate, in this case the neuron remains silent as expected from our observation in Figure 4B.
All inputs activate, in this last case the neuron firing rate remains moderate because of the refractory period.

This figure thus presents the response of the neuron model to all non-trivial cases, we have only omitted the case without any input activation (and therefore without any output activity).

Finally, we show an implementation of the spike interpretation in Figure 6. This model is identical to the model shown previously (Figure 5), except for a slightly lower activation threshold of the sodium channels (V_T = −55 mV instead of V_T = −50 mV) to make it spike more easily. We discretize time into bins of 25 ms and decide randomly for each input whether it is active in each bin. If it is active, it activates at the beginning of the bin with a small temporal jitter (1 ms); inputs activating in the same bin therefore spike coincidentally. We can directly link these activations to Boolean variables that are either 0 (no spike) or 1 (spike). As Figure 6 shows, the neuron implements the D-AND and only spikes whenever the black synapses activate together with at least one of the blue or green synapses.

Figure 6. A biophysical model implementing the Dominant AND (spike interpretation).

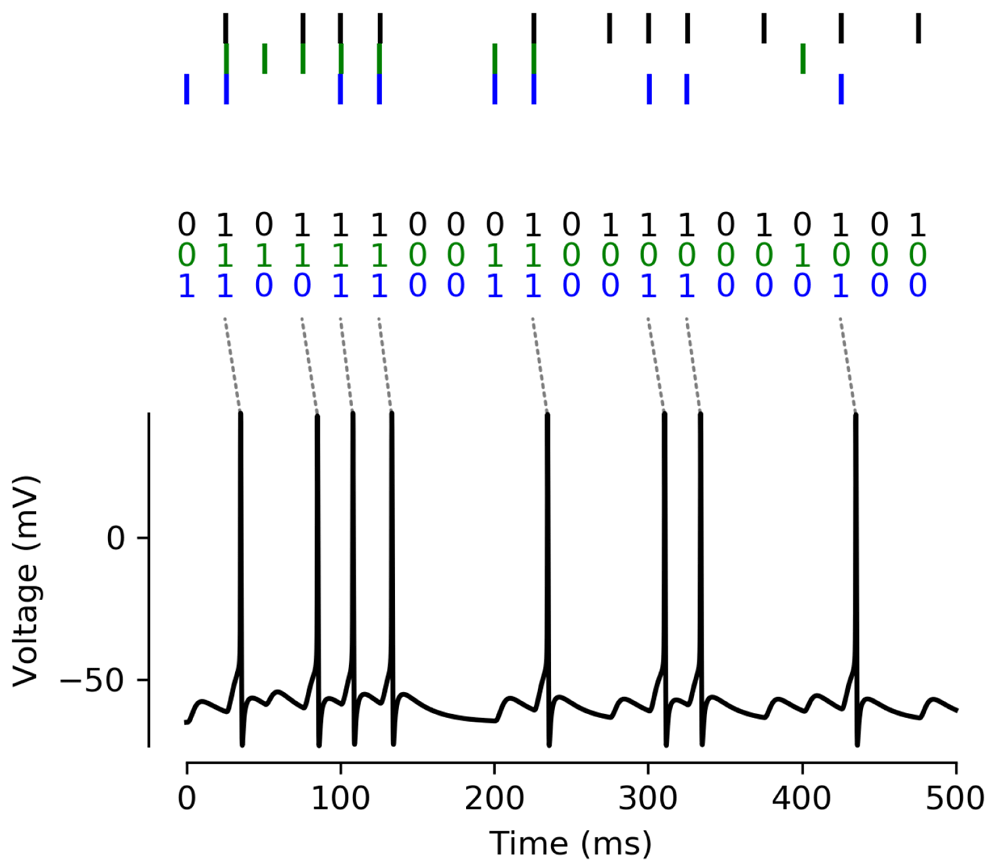
Top: The biophysical model receives input from three sources, where activation happens at regular intervals of 25 ms, with a random jitter of ±1ms for each spike. We translate this activity into a binary pattern for each time bin of 25 ms. Bottom: The model’s membrane potential as measured in the soma. The response spikes implement the output of the D-AND computation as described in Table 2.

We have shown that a biophysical model can implement the D-AND computation using a different strategy than the LTU. Each input has the same synaptic weight producing the same depolarisation at the soma. To distinguish between the inputs, the biophysical model uses location instead of strength: the dominant input (black) targets its own dendrite, while the two other inputs cluster on the same dendrite. With this strategy, the model can implement the D-AND. This implementation also works for two interpretations of the Boolean inputs and outputs – as elevated rates of spiking without temporal alignment, or as precisely timed coincident spikes.

Discussion

In the present work, we extend the linear threshold unit (LTU) to the sub-linear threshold unit (SLTU), a more realistic neuron model that includes non-linear processing in dendrites. We compare these two models on the implementation of a simple computation, the D-AND. We define it for three inputs and then extend it to n inputs by keeping its two defining features: a single dominant input that needs to be activated together with at least one of the remaining inputs. In this extension, the synaptic heterogeneity - e.g. the number of distinct binary synapses - grows linearly with n in the case of an LTU implementation while all synaptic weights remain equal for an SLTU with two dendrites.

For instance, if n = 1000 a single pre-synaptic input needs to make 999 synaptic contacts to implement the D-AND with a LTU while a single binary synapse suffices for a SLTU. This example demonstrates that a SLTU can implement the D-AND more efficiently -with less binary synapse - than the LTU.

Our denomination of one input as “dominant” and the others as “non-dominant” in the definition of the D-AND relates to the distinction between “driver” and “modulator” inputs²⁰. This concept, where driver inputs are necessary to activate a neuron, but this activity can be modulated by other inputs, is ubiquitous in the sensory system. For example, neurons in the primary visual cortex require a stimulus in their classical receptive field. Stimuli in the so-called extra-classical receptive field cannot activate the neuron by themselves, but strongly modulate the response if presented together with a stimulus in the classical receptive field²¹. This distinction is not entirely applicable for the D-AND, since the dominant input X₁ is not sufficient to activate the neuron by itself. Nevertheless, both computations rely on making a distinction between synaptic inputs, which can be implemented by placing inputs on different dendrites as we have shown in this study.

We show in a previous study that STLUs enable one to robustly implement a computation²². In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. Alike the present work we exploited the placement of the synapses rather than the magnitude of their weight to implement the computation.

Several properties of our biophysical model used here fit with experimental observations. Firstly, synapses at different positions tend to create the same depolarisation at the soma¹⁸. Secondly, while the depolarisation generated at a dendritic tip could be large (>50mV) the depolarisation recorded at the soma never exceeds 10mV. Finally, many experimental studies show examples of sub-linear summation in dendrites^8,9, notably in interneurons.

How could neurons learn to implement the D-AND in an STLU? Multiple studies have shown that synaptic rewiring can happen at the sub-cellular level in a short time period²³ and that such a reorganisation could be used for learning²⁴. This markedly differs from classic Hebbian learning which uses changes in the total synaptic weight to implement computations.

Our biophysical model respects two important experimental observations. First, all synapses taken individually produce the same depolarisation at the soma, the so-called "synaptic democracy" like in 18. Second, several experimental studies show examples of sub-linear summationin dendrites¹⁰, notably in interneurons^8,9.

How could neurons learn to implement the D-AND in an SLTU? Multiple studies have shown that synaptic rewiring can happen at the sub-cellular level in a short time period²³ and that such a reorganisation could be used for learning²⁴. This markedly differs from classic Hebbian learning which uses changes in the total synaptic weight to implement computations, a SLTU friendly learning algorithm would keep the total synaptic weight constant while changing the targeted dendrites.

Our findings also have implications beyond neuroscience, in particular for engineering applications. Studies in computer science assert that even problems solvable by an LTU might not have a solution when weights have a limited precision²⁵. Being able to implement computations with an SLTU is therefore advantageous for hardware with limited resources.

In conclusion, dendrites unlock computations inaccessible without them and allow one to more efficiently implement the accessible ones. For instance, to implement the D-AND when n=1001 a SLTU needs a single synaptic contact for the dominant input while a LTU requires a thousand. Dendrites enable us to do more with less.

Author contributions statement

R.C. wrote the initial draft, initiated the project, and made the initial simulations and figures. M.S. added additional simulations and improved part of the simulation code. Both authors discussed the results and wrote the final manuscript.

Acknowledgements

This project started a long time ago within a team directed by Alain Destexhe and stems from multiple discussions with B. Teleńczuk. We also want to thank F. Danneville and C. Loyez for the stimulant discussions, Prof. A. Cappy for his remarks on the method, and M. Humphries for numerous valuable comments. Finally we want to thank A. Foust for making our scientific English easier to read and Ms Marini-Audouard for the proof-reading before submission.

Faculty Opinions recommended

References

1. McCulloch WS, Pitts W: A logical calculus of the ideas immanent in nervous activity. 1943. Bull Math Biol. 1990; 52(1–2): 99–115; discussion 73–97. PubMed Abstract | Publisher Full Text
2. Minsky M, Papert SA: Perceptrons: an introduction to computational geometry. MIT Press, Cambridge Mass, 1957.
3. Cybenko G: Approximation by superpositions of a sigmoidal function. Math Control Signal Systems. 1989; 2(4): 303–314. Publisher Full Text
4. Håstad J: On the Size of Weights for Threshold Gates. SIAM J Discrete Math. 1994; 7(3): 484–492. Publisher Full Text
5. Muroga S: Threshold logic and its applications. Wiley-Interscience, New York, 1971. Reference Source
6. Pfeil T, Potjans TC, Schrader S, et al.: Is a 4-Bit Synaptic Weight Resolution Enough? Constraints on Enabling Spike-Timing Dependent Plasticity in Neuromorphic Hardware. Front Neurosci. 2012; 6: 90. PubMed Abstract | Publisher Full Text | Free Full Text
7. Poirazi P, Brannon T, Mel BW: Pyramidal Neuron as Two-Layer Neural Network. Neuron. 2003; 37(6): 989–999. PubMed Abstract | Publisher Full Text
8. Tzilivaki A, Kastellakis G, Poirazi P: Challenging the point neuron dogma: FS basket cells as 2-stage nonlinear integrators. Nat Commun. 2019; 10(1): 3664. PubMed Abstract | Publisher Full Text | Free Full Text
9. Abrahamsson T, Cathala L, Matsui K, et al.: Thin Dendrites of Cerebellar Interneurons Confer Sublinear Synaptic Integration and a Gradient of Short-Term Plasticity. Neuron. 2012; 73(6): 1159–1172. PubMed Abstract | Publisher Full Text
10. Polsky A, Mel BW, Schiller J: Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci. 2004; 7(6): 621–7. PubMed Abstract | Publisher Full Text
11. Cazé RD, Humphries MD, Gutkin B: Spiking and saturating dendrites differentially expand single neuron computation capacity. NIPS. 2012; 1070–1078. Reference Source
12. Gidon A, Zolnik TA, Fidzinski P, et al.: Dendritic action potentials and computation in human layer 2/3 cortical neurons. Science. 2020; 367(6473): 83–87. PubMed Abstract | Publisher Full Text
13. Ujfalussy BB, Makara JK, Branco T, et al.: Dendritic nonlinearities are tuned for efficient spike-based computations in cortical circuits. eLife. eLife Sciences Publications, Ltd. 2015; 4: e10056. PubMed Abstract | Publisher Full Text | Free Full Text
14. Traub RD, Miles R: Neuronal Networks of the Hippocampus. Cambridge University Press, May 1991. Publisher Full Text
15. Stimberg M, Brette R, Goodman DFM: Brian 2, an intuitive and efficient neural simulator. eLife. 2019; 8: e47314. PubMed Abstract | Publisher Full Text | Free Full Text
16. Cazé RD, Stimberg M: Source code for publication "Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights" (Version 2020.12). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.4315011
17. Koch C, Segev I: The role of single neurons in information processing. Nat Neurosci. 2000; 3 Suppl: 1171–1177. PubMed Abstract | Publisher Full Text
18. Magee JC, Cook EP: Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat Neurosci. 2000; 3(9): 895–903. PubMed Abstract | Publisher Full Text
19. Behabadi BF, Mel BW: Mechanisms underlying subunit independence in pyramidal neuron dendrites. Proc Natl Acad Sci U S A. 2014; 111(1): 498–503. PubMed Abstract | Publisher Full Text | Free Full Text
20. Sherman SM, Guillery RW: On the actions that one nerve cell can have on another: distinguishing “drivers” from “modulators”. Proc Natl Acad Sci U S A. 1998; 95(12): 7121–7126. PubMed Abstract | Publisher Full Text | Free Full Text
21. Hubel DH, Wiesel TN: Receptive fields and functional architecture in two nonstriate visual areas (18 and 19) of the cat. J Neurophysiol. 1965; 28(2): 229–289. PubMed Abstract | Publisher Full Text
22. Cazé RD, Jarvis S, Foust AJ, et al.: Dendrites Enable a Robust Mechanism for neuronal stimulus selectivity. Neural Comput. 2017; 29(9): 2511–2527. PubMed Abstract | Publisher Full Text
23. Fu M, Yu X, Lu J, et al.: Repetitive motor learning induces coordinated formation of clustered dendritic spines in vivo. Nature. 2012; 483(7387): 92–95. PubMed Abstract | Publisher Full Text | Free Full Text
24. Limbacher T, Legenstein R: Emergence of Stable Synaptic Clusters on Dendrites Through Synaptic Rewiring. Front Comput Neurosci. 2020; 14: 57. PubMed Abstract | Publisher Full Text | Free Full Text
25. Draghici S: On the capabilities of neural networks using limited precision weights. Neural Netw. 2002; 15(3): 395–414. PubMed Abstract | Publisher Full Text

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 28 Sep 2020

Author details Author details

¹ IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France
² Institut de la vision, CNRS, INSERM, Paris, 75012, France

Romain D. Cazé
Roles: Conceptualization, Formal Analysis, Investigation, Methodology, Project Administration, Resources, Software, Validation, Visualization, Writing – Original Draft Preparation

Marcel Stimberg
Roles: Funding Acquisition, Investigation, Methodology, Software, Validation, Visualization, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by the following grants: LabEx LIFESENSES (ANR-10-LABX-65) and IHU FOReSIGHT (ANR-18-IAHU-01).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (3)

version 3

Revised

Published: 18 Apr 2021, 9:1174

https://doi.org/10.12688/f1000research.26486.3

version 2

Revised

Published: 20 Jan 2021, 9:1174

https://doi.org/10.12688/f1000research.26486.2

version 1

Published: 28 Sep 2020, 9:1174

https://doi.org/10.12688/f1000research.26486.1

© 2021 Cazé RD and Stimberg M. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Cazé RD and Stimberg M. Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights [version 3; peer review: 3 approved]. F1000Research 2021, 9:1174 (https://doi.org/10.12688/f1000research.26486.3)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 3

VERSION 3

PUBLISHED 18 Apr 2021

Revised

Views

Reviewer Report 20 Apr 2021

Fleur Zeldenrust, Department of Neurophysiology, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, The Netherlands

Approved

https://doi.org/10.5256/f1000research.55803.r83470

This paper shows, by fundamental derivation and simulations, that a certain class of neural computations can be more efficiently and realistically be implemented by neurons with dendrites than without dendrites. This is relevant and timely, as there has recently been an increased interest in dendritic computation, both from neuroscience and from neuromorphic computing. It is also a logical follow-up of the first author’s previous work, as mentioned in the discussion. I really appreciate the way of abstracting the neural computations to Boolean functions, as they also did in their previous work, which makes the work fundamental and generally applicable. The general setup of the paper is clear and appropriate, and the derivations and simulations are done correctly and clearly. My previous comments and concerns have all been addressed, and I now happily approve of this version.

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational neuroscience

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Version 2

VERSION 2

PUBLISHED 20 Jan 2021

Revised

Views

Reviewer Report 10 Mar 2021

Sacha van Albada, Institute of Neuroscience and Medicine (INM-6), Research Centre Jülich, Germany; Institute of Zoology, University of Cologne, Germany

Approved

https://doi.org/10.5256/f1000research.50405.r77773

I am happy with the changes and have no more comments on the content.

I only still have a few tiny corrections:

p. 3 “where most of the synapses lay” → “where most of ... Continue reading

CITE

Report a concern

Reader Comment 01 Apr 2021

Romain Cazé, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

01 Apr 2021

Reader Comment

We took care of all corrections and we want to thank again the reviewer for her constructive remarks.
Competing Interests: No competing interests were disclosed.
We took care of all corrections and we want to thank again the reviewer for her constructive remarks.
We took care of all corrections and we want to thank again the reviewer for her constructive remarks.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Reader Comment 01 Apr 2021

Romain Cazé, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

01 Apr 2021

Reader Comment

We took care of all corrections and we want to thank again the reviewer for her constructive remarks.
Competing Interests: No competing interests were disclosed.
We took care of all corrections and we want to thank again the reviewer for her constructive remarks.
We took care of all corrections and we want to thank again the reviewer for her constructive remarks.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 29 Jan 2021

Fleur Zeldenrust, Department of Neurophysiology, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, The Netherlands

Approved

https://doi.org/10.5256/f1000research.50405.r77774

I appreciate the work the authors put in rewriting the text and reorganising the figures. I still think it is a nice and relevant story. I only have a few textual clarifications left.

Figure 4:
I appreciate the reorganisation of the figure, and the addition of the ‘gray line’, but I think the caption and legend need to explain it a bit better. ‘Linear summation’ is not mentioned in the figure caption. More specifically:
a/b) I see a white synapse, not a black one?
b) I see only black-dashed and/or grey, not a black line?
“ In a linear neuron, all active groups of synapses (black + blue or black + green or blue + green) produce the same somatic EPSP (gray dotted line). “ — What does this mean? I see a clear difference between the aquamarine line and the black grey dashed line, but I don’t understand this sentence. Maybe you could specify how many synapses are activated?
c) I don’t understand the difference between the first (black line — as far as I understand green+white or blue+white) and the second (green+white). Or the difference between the last (blue and green) and the penultimate (blue +green). I also don’t see the gray dashed line in C.

Figure 5:
I appreciate the improved explanation of what was what, but I had to read this sentence a few times
“(gray: no synapse/only black/green/blue, green: black + green, blue: black + blue, aquamarine: green + blue, black: all inputs active)”
Also, as it is basically the same setup as in Fig 4 (right?), this might be mentioned.
“With linear summation these three input patterns would evoke identical responses.” -- I would add something like: ‘either all three would elicit not response (i.e. aquamarine line) or all three would electie a response (blue or green lines).

Discussion:

In the present work, we oppose the linear threshold unit (LTU) to the sub-linear threshold unit (SLTU),— I don’t think you ‘oppose’ the LTU, you rather extend it.
Remove ‘the’ before non-linear processing
I appreciate the use of ‘heterogeneity’, but I think the term ‘synaptic heterogeneity’ needs to be defined — this term is used for the first time in the discussion as such, and needs a bit explanation here. Also, it needs to be explained here why the growth of the heterogeneity can be considered a problem (that needs to be solved by using for instance your SLTU).
“Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.
‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!
Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.
Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational neuroscience

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Reader Comment 01 Apr 2021

Romain Cazé, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

01 Apr 2021

Reader Comment

We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic ... Continue reading We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic heterogeneity: for instance the number of binary synapse an input needs to make, it might also be the number of synaptic states or the raw number of synapses.

> “Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.

We corrected the paragraph to make the parallel between the two studies clearer

> ‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!

We rewrote the paragraph to make the first and the last point clearer than before and we removed the superfluous point.

> Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.

We precised how a SLTU friendly learning algorithm would differ from a classic Hebbian learning algorithm.

> Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

We now insist on this point by providing a concrete example: To implement the D-AND when n=1001 a SLTU needs a single synaptic contact for the dominant input while a LTU requires a thousand.

We want to thank again the reviewer: her question and remarks made our article clearer.
We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic heterogeneity: for instance the number of binary synapse an input needs to make, it might also be the number of synaptic states or the raw number of synapses.

> “Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.

We corrected the paragraph to make the parallel between the two studies clearer

> ‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!

We rewrote the paragraph to make the first and the last point clearer than before and we removed the superfluous point.

> Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.

We precised how a SLTU friendly learning algorithm would differ from a classic Hebbian learning algorithm.

> Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

We now insist on this point by providing a concrete example: To implement the D-AND when n=1001 a SLTU needs a single synaptic contact for the dominant input while a LTU requires a thousand.

We want to thank again the reviewer: her question and remarks made our article clearer.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Reader Comment 01 Apr 2021

Romain Cazé, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

01 Apr 2021

Reader Comment

We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic ... Continue reading We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic heterogeneity: for instance the number of binary synapse an input needs to make, it might also be the number of synaptic states or the raw number of synapses.

> “Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.

We corrected the paragraph to make the parallel between the two studies clearer

> ‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!

We rewrote the paragraph to make the first and the last point clearer than before and we removed the superfluous point.

> Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.

We precised how a SLTU friendly learning algorithm would differ from a classic Hebbian learning algorithm.

> Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

We now insist on this point by providing a concrete example: To implement the D-AND when n=1001 a SLTU needs a single synaptic contact for the dominant input while a LTU requires a thousand.

We want to thank again the reviewer: her question and remarks made our article clearer.
We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic heterogeneity: for instance the number of binary synapse an input needs to make, it might also be the number of synaptic states or the raw number of synapses.

> “Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.

We corrected the paragraph to make the parallel between the two studies clearer

> ‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!

We rewrote the paragraph to make the first and the last point clearer than before and we removed the superfluous point.

> Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.

We precised how a SLTU friendly learning algorithm would differ from a classic Hebbian learning algorithm.

> Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

We now insist on this point by providing a concrete example: To implement the D-AND when n=1001 a SLTU needs a single synaptic contact for the dominant input while a LTU requires a thousand.

We want to thank again the reviewer: her question and remarks made our article clearer.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 29 Jan 2021

Alexandra Tzilivaki, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

Panayiota Poirazi, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

Approved

https://doi.org/10.5256/f1000research.50405.r77772

The authors have successfully addressed ... Continue reading

CITE

Report a concern

Reader Comment 01 Apr 2021

Romain Cazé, CNRS UMR 8520, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

01 Apr 2021

Reader Comment

We want to thank again the reviewer for her contribution.
Competing Interests: No competing interests were disclosed.
We want to thank again the reviewer for her contribution.
We want to thank again the reviewer for her contribution.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Reader Comment 01 Apr 2021

Romain Cazé, CNRS UMR 8520, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

01 Apr 2021

Reader Comment

We want to thank again the reviewer for her contribution.
Competing Interests: No competing interests were disclosed.
We want to thank again the reviewer for her contribution.
We want to thank again the reviewer for her contribution.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Version 1

VERSION 1

PUBLISHED 28 Sep 2020

Views

Reviewer Report 27 Oct 2020

Alexandra Tzilivaki, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

Panayiota Poirazi, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

Approved with Reservations

https://doi.org/10.5256/f1000research.29243.r72169

In this modelling work, Caze and Stimberg propose that dendrites can efficiently decrease the weight resolution required to perform linear separable functions, something that is difficult to achieve using an LTU. The code that generates the model/data shown in figures is available and can be executed smoothly. All in all, the paper is a good fit for the F1000 Research. The results have the potential to advance the implementation of ANNs and neuromorphic hardware. Thus, it applies both to neuroscientific and computer science community.

Suggestions:

The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).
What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".
The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: computational neuroscience, dendrites

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

CITE

Report a concern

Author Response 22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

22 Jan 2021

Author Response

*The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply ... Continue reading *The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).*

The results we present do not depend on model details, the only mandatory feature is the sub-linear summation in the dendrite. To further emphasize this point, we have added an exploration of the synaptic weight parameter in Fig.4 and discuss how it shows the robustness of the approach. Also note that the simulation code we provide can reproduce the basic results with a simple integrate-and-fire neuron model, further showing the robustness of the results.

*What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".*

In general, introducing negative weights will require the weights of other synapses to be higher in order to compensate. Be aware that the D-AND function cannot be implemented (neither in the LTU nor in the SLTU) if one of the inputs only connects with a single synapse that has a negative weight. This is because for each input, there is at least one configuration of the other inputs where switching that specific input from 0 to 1 needs to switch the output result from 0 to 1. If it only connects with a negative weight, this is not possible.

*The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".*

We have changed the title to “Neurons with dendrites” to avoid any possible confusion.
*The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).*

The results we present do not depend on model details, the only mandatory feature is the sub-linear summation in the dendrite. To further emphasize this point, we have added an exploration of the synaptic weight parameter in Fig.4 and discuss how it shows the robustness of the approach. Also note that the simulation code we provide can reproduce the basic results with a simple integrate-and-fire neuron model, further showing the robustness of the results.

*What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".*

In general, introducing negative weights will require the weights of other synapses to be higher in order to compensate. Be aware that the D-AND function cannot be implemented (neither in the LTU nor in the SLTU) if one of the inputs only connects with a single synapse that has a negative weight. This is because for each input, there is at least one configuration of the other inputs where switching that specific input from 0 to 1 needs to switch the output result from 0 to 1. If it only connects with a negative weight, this is not possible.

*The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".*

We have changed the title to “Neurons with dendrites” to avoid any possible confusion.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

22 Jan 2021

Author Response

*The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply ... Continue reading *The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).*

The results we present do not depend on model details, the only mandatory feature is the sub-linear summation in the dendrite. To further emphasize this point, we have added an exploration of the synaptic weight parameter in Fig.4 and discuss how it shows the robustness of the approach. Also note that the simulation code we provide can reproduce the basic results with a simple integrate-and-fire neuron model, further showing the robustness of the results.

*What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".*

In general, introducing negative weights will require the weights of other synapses to be higher in order to compensate. Be aware that the D-AND function cannot be implemented (neither in the LTU nor in the SLTU) if one of the inputs only connects with a single synapse that has a negative weight. This is because for each input, there is at least one configuration of the other inputs where switching that specific input from 0 to 1 needs to switch the output result from 0 to 1. If it only connects with a negative weight, this is not possible.

*The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".*

We have changed the title to “Neurons with dendrites” to avoid any possible confusion.
*The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).*

The results we present do not depend on model details, the only mandatory feature is the sub-linear summation in the dendrite. To further emphasize this point, we have added an exploration of the synaptic weight parameter in Fig.4 and discuss how it shows the robustness of the approach. Also note that the simulation code we provide can reproduce the basic results with a simple integrate-and-fire neuron model, further showing the robustness of the results.

*What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".*

In general, introducing negative weights will require the weights of other synapses to be higher in order to compensate. Be aware that the D-AND function cannot be implemented (neither in the LTU nor in the SLTU) if one of the inputs only connects with a single synapse that has a negative weight. This is because for each input, there is at least one configuration of the other inputs where switching that specific input from 0 to 1 needs to switch the output result from 0 to 1. If it only connects with a negative weight, this is not possible.

*The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".*

We have changed the title to “Neurons with dendrites” to avoid any possible confusion.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 23 Oct 2020

Fleur Zeldenrust, Department of Neurophysiology, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, The Netherlands

Approved with Reservations

https://doi.org/10.5256/f1000research.29243.r72167

This paper shows, by fundamental derivation and simulations, that a certain class of neural computations can be more efficiently and realistically be implemented by neurons with dendrites than without dendrites. This is relevant and timely, as there has recently been an increased interest in dendritic computation, both from neuroscience and from neuromorphic computing. It is also a logical follow-up of the first author’s previous work, as mentioned in the discussion. I really appreciate the way of abstracting the neural computations to Boolean functions, as they also did in their previous work, which makes the work fundamental and generally applicable. The general setup of the paper is clear and appropriate, and the derivations and simulations are done correctly and clearly. My main comments are minor and concern the presentation, concerning the language, some further explanations and a few citations. I will add them in detail below. Overall, if these minor edits are addressed I wholeheartedly recommend this paper.

Detailed comments:

P. 3

“a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?
The formula you give for integer-valued weights does not give integer values? And n is not defined.
The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.
“Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’
“Dendrites are the receptive elementS of neurons where most of the receiving synapses lay.”
“They enable neurons to compute linearly inseparable computationS”
“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.
“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.
“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’
“and connect to the soma at their extremity” at ONE extremity.
Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)
Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

P. 4

“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.
“peculiarities” replace with something like ‘the specific implementation’
Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.
Definition 5: there are a few things unclear to me:
- θ is defined but not used. Shouldn’t that be in the definition of E?
- If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?
- Y is not defined
- I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper
“computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?
“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?

P. 5

“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before
“Here we always use” add comma between here and we
Do not start a paragraph with ‘Then’. Also, ‘Next’ might be better
“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?
“Here, the dominance of X0 is only expressed by its placement.” Please explain more
Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’

P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.
Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’
Figure 4
- These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?
- “…Membrane voltage traces responding…” a voltage trace does not respond.
- “…locations (dendrite …” -> “ locations (at the dendrite…”
- The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?
- It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites
Figure 5
- Legend: part explaining the top should not be bold.
- Top (activity of the inputs): for what input it this? 111?
- It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

P. 7

Proof: there are two different fonts for Theta
I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.
Merge paragraphs (i.e. delete white line) ending with ‘…sublinear summation.’, ‘…at the soma.’ and ‘…response.’.
Replace ; with , after individually.
Add ‘-‘ with back propagation, or make one word.

P. 8

Merge paragraphs (i.e. delete white line) ending with ‘…spike interpretation.’
Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?
Merge paragraphs (i.e. delete white line) ending with ‘…remain equal.’
“The first two Results sections look at a computation and one of its possible extension”-> “In the first two sections in the Results we describe an example of a computation and one of its possible extentionS “ (a section does not look)
“We think that the extension we chose is a reasonable one” Why? Please explain
“Note also that…” do not start a paragraph that way.
“Our study also relateS…”
The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?
Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational neuroscience

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

22 Jan 2021

Author Response

We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply ... Continue reading We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply below (original reviewer comments in italics):

*a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?*

We decided not to go into details about the structure of such networks and therefore used "sufficiently large" to both encompass width and depth of the network. We now cite the study by G. Cybenko which (to our knowledge) is one of the first demonstrations of the finding.

*The formula you give for integer-valued weights does not give integer values? And n is not defined.*

We have decided to no longer give the full formula, since its details are not relevant to our study (the formula could indeed give non-integer values, but it only established a lower bound). We now only state that the Hastad et al. “studied a computation implementable by an LTU only if its synaptic weight resolution grows exponentially with the number of inputs.”

*The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.*

We have removed the consufing use of the word ‘means’ and replaced it by ‘resources’.

*Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’*

We rewrote the paragraph to clarify our point (a large number of resources in LTU-based neuromorphic chips have to be dedicated to synapses).

*“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.*

We have rewritten the paragraph to make it clearer. The “three input variable computations” did not refer to three computations, but to computations of three input variables. We have rephrased this as “computations of three input variables” to avoid confusion.

*“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.*

We have precise this point by stating that the implementation uses “fewer synapses”.

*“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’*

We have changed this sentence to state that the work “proposes a new role”.

“and connect to the soma at their extremity” at ONE extremity.

We have change the sentence accordingly.

    Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)

    Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

We have merged the paragraphs and slightly changed the text surrounding the equations.

P. 4

*“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.*

Yes, The code in the repo can run both models. We have changed the text to make this point clearer.

* “peculiarities” replace with something like ‘the specific implementation’*

We have changed the text accordingly

* Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.*

One vector is superior to another if all of its component are superior. This is specified as part of the definition (“meaning that for all i…”)

*Definition 5: there are a few things unclear to me:
        θ is defined but not used. Shouldn’t that be in the definition of E?*

Thank you for pointing this out. The θ was indeed meant to be the threshold in the function E, but for our purposes a fixed value of 1 is enough. We have therefore removed θ from the definition.

*If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?*

This is correct and we now mention this in the text.

*Y is not defined*

This was a printing error, Y is the argument of the function E (instead of X). We have corrected this.


* I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper*

The summation is sublinear due to the saturation of the function E, which is the simplest (and strongest) sublinear summation: E(1) = 1, but E(1 + 1) = E(1 + 1 + …) = 1 as well. The shape of the function is now more clearly depicted in Figures 2 and 3.

* “computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?*

We have rewritten this paragraph to make it clearer and now use ‘heterogeneous’ instead of ‘different’.


*“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?*

The table only lists positive threshold functions (or, equivalently, functions implementable by an LTU with non-negative weights), not all random combinations have this property. We have explained this more clearly in the rewritten paragraph.

*P. 5*

*“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before*

Our statement refers to both computations, we have rewritten the sentence to make this explicit.

*“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?*

Yes, we have changed the sentence to refer to the driving force here as well.

*“Here, the dominance of X0 is only expressed by its placement.” Please explain more*

We have expanded the explanation of the mechanisms used by the SLTU vs. the LTU.

*Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to the definition of the function E in Def. 5.

*P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.*

We agree that this sentence was confusing and have removed it.

*Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to Def. 5 in the caption.

*Figure 4
These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?*

These EPSPs were measured in the dendrite. When they are measured in the soma they are around 10mV and therefore more biologically realistic. While our reorganized Figure 4 no longer shows the EPSP measured at the dendrite, we now mention this point in the discussion.

*The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?*

In our reorganized figure, the arrows are no longer needed.

*It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites*

The reorganized Figure 4 now shows linear summation (i.e., without saturation) as a gray dotted line.

    Figure 5
        Legend: part explaining the top should not be bold.

        Top (activity of the inputs): for what input it this? 111?

        It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

We corrected the mistake in the caption and add a final sentence to explain what would happen in a point neuron: all the voltage responses (clustered or scattered) would be equal.

*P. 7*

*Proof: there are two different fonts for Theta*

Thank you for alerting us to this issue, we will watch out for it in the revision proof.

*I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.*

We agree and have removed the paragraph.

*P. 8*

*Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?*

Yes, an “active synapse” receives 25 spikes over 250ms (i.e. a 100Hz input) and “inactive synapses” do not receive any spikes. We now point this out in the Figure caption and changed the text to make it clearer.

*“We think that the extension we chose is a reasonable one” Why? Please explain*

We have removed this sentence and instead now include a sentence describing the features of the function that are preserved by extending it in the way we did.

*The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?*

We have rewritten parts of the Discussion to make it more fluent.

*Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?*

We have added a paragraph discussing the issue of plasticity to the discussion. We thank the reviewer for alerting us to a number of typos (missing ‘s’ at the end of words, missing commas, etc.) and language issues which we have corrected in the revised manuscript.
We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply below (original reviewer comments in italics):

*a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?*

We decided not to go into details about the structure of such networks and therefore used "sufficiently large" to both encompass width and depth of the network. We now cite the study by G. Cybenko which (to our knowledge) is one of the first demonstrations of the finding.

*The formula you give for integer-valued weights does not give integer values? And n is not defined.*

We have decided to no longer give the full formula, since its details are not relevant to our study (the formula could indeed give non-integer values, but it only established a lower bound). We now only state that the Hastad et al. “studied a computation implementable by an LTU only if its synaptic weight resolution grows exponentially with the number of inputs.”

*The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.*

We have removed the consufing use of the word ‘means’ and replaced it by ‘resources’.

*Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’*

We rewrote the paragraph to clarify our point (a large number of resources in LTU-based neuromorphic chips have to be dedicated to synapses).

*“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.*

We have rewritten the paragraph to make it clearer. The “three input variable computations” did not refer to three computations, but to computations of three input variables. We have rephrased this as “computations of three input variables” to avoid confusion.

*“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.*

We have precise this point by stating that the implementation uses “fewer synapses”.

*“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’*

We have changed this sentence to state that the work “proposes a new role”.

“and connect to the soma at their extremity” at ONE extremity.

We have change the sentence accordingly.

    Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)

    Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

We have merged the paragraphs and slightly changed the text surrounding the equations.

P. 4

*“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.*

Yes, The code in the repo can run both models. We have changed the text to make this point clearer.

* “peculiarities” replace with something like ‘the specific implementation’*

We have changed the text accordingly

* Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.*

One vector is superior to another if all of its component are superior. This is specified as part of the definition (“meaning that for all i…”)

*Definition 5: there are a few things unclear to me:
        θ is defined but not used. Shouldn’t that be in the definition of E?*

Thank you for pointing this out. The θ was indeed meant to be the threshold in the function E, but for our purposes a fixed value of 1 is enough. We have therefore removed θ from the definition.

*If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?*

This is correct and we now mention this in the text.

*Y is not defined*

This was a printing error, Y is the argument of the function E (instead of X). We have corrected this.


* I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper*

The summation is sublinear due to the saturation of the function E, which is the simplest (and strongest) sublinear summation: E(1) = 1, but E(1 + 1) = E(1 + 1 + …) = 1 as well. The shape of the function is now more clearly depicted in Figures 2 and 3.

* “computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?*

We have rewritten this paragraph to make it clearer and now use ‘heterogeneous’ instead of ‘different’.


*“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?*

The table only lists positive threshold functions (or, equivalently, functions implementable by an LTU with non-negative weights), not all random combinations have this property. We have explained this more clearly in the rewritten paragraph.

*P. 5*

*“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before*

Our statement refers to both computations, we have rewritten the sentence to make this explicit.

*“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?*

Yes, we have changed the sentence to refer to the driving force here as well.

*“Here, the dominance of X0 is only expressed by its placement.” Please explain more*

We have expanded the explanation of the mechanisms used by the SLTU vs. the LTU.

*Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to the definition of the function E in Def. 5.

*P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.*

We agree that this sentence was confusing and have removed it.

*Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to Def. 5 in the caption.

*Figure 4
These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?*

These EPSPs were measured in the dendrite. When they are measured in the soma they are around 10mV and therefore more biologically realistic. While our reorganized Figure 4 no longer shows the EPSP measured at the dendrite, we now mention this point in the discussion.

*The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?*

In our reorganized figure, the arrows are no longer needed.

*It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites*

The reorganized Figure 4 now shows linear summation (i.e., without saturation) as a gray dotted line.

    Figure 5
        Legend: part explaining the top should not be bold.

        Top (activity of the inputs): for what input it this? 111?

        It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

We corrected the mistake in the caption and add a final sentence to explain what would happen in a point neuron: all the voltage responses (clustered or scattered) would be equal.

*P. 7*

*Proof: there are two different fonts for Theta*

Thank you for alerting us to this issue, we will watch out for it in the revision proof.

*I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.*

We agree and have removed the paragraph.

*P. 8*

*Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?*

Yes, an “active synapse” receives 25 spikes over 250ms (i.e. a 100Hz input) and “inactive synapses” do not receive any spikes. We now point this out in the Figure caption and changed the text to make it clearer.

*“We think that the extension we chose is a reasonable one” Why? Please explain*

We have removed this sentence and instead now include a sentence describing the features of the function that are preserved by extending it in the way we did.

*The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?*

We have rewritten parts of the Discussion to make it more fluent.

*Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?*

We have added a paragraph discussing the issue of plasticity to the discussion. We thank the reviewer for alerting us to a number of typos (missing ‘s’ at the end of words, missing commas, etc.) and language issues which we have corrected in the revised manuscript.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

22 Jan 2021

Author Response

We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply ... Continue reading We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply below (original reviewer comments in italics):

*a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?*

We decided not to go into details about the structure of such networks and therefore used "sufficiently large" to both encompass width and depth of the network. We now cite the study by G. Cybenko which (to our knowledge) is one of the first demonstrations of the finding.

*The formula you give for integer-valued weights does not give integer values? And n is not defined.*

We have decided to no longer give the full formula, since its details are not relevant to our study (the formula could indeed give non-integer values, but it only established a lower bound). We now only state that the Hastad et al. “studied a computation implementable by an LTU only if its synaptic weight resolution grows exponentially with the number of inputs.”

*The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.*

We have removed the consufing use of the word ‘means’ and replaced it by ‘resources’.

*Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’*

We rewrote the paragraph to clarify our point (a large number of resources in LTU-based neuromorphic chips have to be dedicated to synapses).

*“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.*

We have rewritten the paragraph to make it clearer. The “three input variable computations” did not refer to three computations, but to computations of three input variables. We have rephrased this as “computations of three input variables” to avoid confusion.

*“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.*

We have precise this point by stating that the implementation uses “fewer synapses”.

*“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’*

We have changed this sentence to state that the work “proposes a new role”.

“and connect to the soma at their extremity” at ONE extremity.

We have change the sentence accordingly.

    Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)

    Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

We have merged the paragraphs and slightly changed the text surrounding the equations.

P. 4

*“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.*

Yes, The code in the repo can run both models. We have changed the text to make this point clearer.

* “peculiarities” replace with something like ‘the specific implementation’*

We have changed the text accordingly

* Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.*

One vector is superior to another if all of its component are superior. This is specified as part of the definition (“meaning that for all i…”)

*Definition 5: there are a few things unclear to me:
        θ is defined but not used. Shouldn’t that be in the definition of E?*

Thank you for pointing this out. The θ was indeed meant to be the threshold in the function E, but for our purposes a fixed value of 1 is enough. We have therefore removed θ from the definition.

*If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?*

This is correct and we now mention this in the text.

*Y is not defined*

This was a printing error, Y is the argument of the function E (instead of X). We have corrected this.


* I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper*

The summation is sublinear due to the saturation of the function E, which is the simplest (and strongest) sublinear summation: E(1) = 1, but E(1 + 1) = E(1 + 1 + …) = 1 as well. The shape of the function is now more clearly depicted in Figures 2 and 3.

* “computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?*

We have rewritten this paragraph to make it clearer and now use ‘heterogeneous’ instead of ‘different’.


*“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?*

The table only lists positive threshold functions (or, equivalently, functions implementable by an LTU with non-negative weights), not all random combinations have this property. We have explained this more clearly in the rewritten paragraph.

*P. 5*

*“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before*

Our statement refers to both computations, we have rewritten the sentence to make this explicit.

*“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?*

Yes, we have changed the sentence to refer to the driving force here as well.

*“Here, the dominance of X0 is only expressed by its placement.” Please explain more*

We have expanded the explanation of the mechanisms used by the SLTU vs. the LTU.

*Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to the definition of the function E in Def. 5.

*P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.*

We agree that this sentence was confusing and have removed it.

*Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to Def. 5 in the caption.

*Figure 4
These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?*

These EPSPs were measured in the dendrite. When they are measured in the soma they are around 10mV and therefore more biologically realistic. While our reorganized Figure 4 no longer shows the EPSP measured at the dendrite, we now mention this point in the discussion.

*The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?*

In our reorganized figure, the arrows are no longer needed.

*It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites*

The reorganized Figure 4 now shows linear summation (i.e., without saturation) as a gray dotted line.

    Figure 5
        Legend: part explaining the top should not be bold.

        Top (activity of the inputs): for what input it this? 111?

        It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

We corrected the mistake in the caption and add a final sentence to explain what would happen in a point neuron: all the voltage responses (clustered or scattered) would be equal.

*P. 7*

*Proof: there are two different fonts for Theta*

Thank you for alerting us to this issue, we will watch out for it in the revision proof.

*I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.*

We agree and have removed the paragraph.

*P. 8*

*Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?*

Yes, an “active synapse” receives 25 spikes over 250ms (i.e. a 100Hz input) and “inactive synapses” do not receive any spikes. We now point this out in the Figure caption and changed the text to make it clearer.

*“We think that the extension we chose is a reasonable one” Why? Please explain*

We have removed this sentence and instead now include a sentence describing the features of the function that are preserved by extending it in the way we did.

*The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?*

We have rewritten parts of the Discussion to make it more fluent.

*Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?*

We have added a paragraph discussing the issue of plasticity to the discussion. We thank the reviewer for alerting us to a number of typos (missing ‘s’ at the end of words, missing commas, etc.) and language issues which we have corrected in the revised manuscript.
We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply below (original reviewer comments in italics):

*a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?*

We decided not to go into details about the structure of such networks and therefore used "sufficiently large" to both encompass width and depth of the network. We now cite the study by G. Cybenko which (to our knowledge) is one of the first demonstrations of the finding.

*The formula you give for integer-valued weights does not give integer values? And n is not defined.*

We have decided to no longer give the full formula, since its details are not relevant to our study (the formula could indeed give non-integer values, but it only established a lower bound). We now only state that the Hastad et al. “studied a computation implementable by an LTU only if its synaptic weight resolution grows exponentially with the number of inputs.”

*The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.*

We have removed the consufing use of the word ‘means’ and replaced it by ‘resources’.

*Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’*

We rewrote the paragraph to clarify our point (a large number of resources in LTU-based neuromorphic chips have to be dedicated to synapses).

*“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.*

We have rewritten the paragraph to make it clearer. The “three input variable computations” did not refer to three computations, but to computations of three input variables. We have rephrased this as “computations of three input variables” to avoid confusion.

*“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.*

We have precise this point by stating that the implementation uses “fewer synapses”.

*“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’*

We have changed this sentence to state that the work “proposes a new role”.

“and connect to the soma at their extremity” at ONE extremity.

We have change the sentence accordingly.

    Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)

    Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

We have merged the paragraphs and slightly changed the text surrounding the equations.

P. 4

*“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.*

Yes, The code in the repo can run both models. We have changed the text to make this point clearer.

* “peculiarities” replace with something like ‘the specific implementation’*

We have changed the text accordingly

* Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.*

One vector is superior to another if all of its component are superior. This is specified as part of the definition (“meaning that for all i…”)

*Definition 5: there are a few things unclear to me:
        θ is defined but not used. Shouldn’t that be in the definition of E?*

Thank you for pointing this out. The θ was indeed meant to be the threshold in the function E, but for our purposes a fixed value of 1 is enough. We have therefore removed θ from the definition.

*If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?*

This is correct and we now mention this in the text.

*Y is not defined*

This was a printing error, Y is the argument of the function E (instead of X). We have corrected this.


* I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper*

The summation is sublinear due to the saturation of the function E, which is the simplest (and strongest) sublinear summation: E(1) = 1, but E(1 + 1) = E(1 + 1 + …) = 1 as well. The shape of the function is now more clearly depicted in Figures 2 and 3.

* “computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?*

We have rewritten this paragraph to make it clearer and now use ‘heterogeneous’ instead of ‘different’.


*“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?*

The table only lists positive threshold functions (or, equivalently, functions implementable by an LTU with non-negative weights), not all random combinations have this property. We have explained this more clearly in the rewritten paragraph.

*P. 5*

*“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before*

Our statement refers to both computations, we have rewritten the sentence to make this explicit.

*“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?*

Yes, we have changed the sentence to refer to the driving force here as well.

*“Here, the dominance of X0 is only expressed by its placement.” Please explain more*

We have expanded the explanation of the mechanisms used by the SLTU vs. the LTU.

*Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to the definition of the function E in Def. 5.

*P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.*

We agree that this sentence was confusing and have removed it.

*Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to Def. 5 in the caption.

*Figure 4
These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?*

These EPSPs were measured in the dendrite. When they are measured in the soma they are around 10mV and therefore more biologically realistic. While our reorganized Figure 4 no longer shows the EPSP measured at the dendrite, we now mention this point in the discussion.

*The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?*

In our reorganized figure, the arrows are no longer needed.

*It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites*

The reorganized Figure 4 now shows linear summation (i.e., without saturation) as a gray dotted line.

    Figure 5
        Legend: part explaining the top should not be bold.

        Top (activity of the inputs): for what input it this? 111?

        It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

We corrected the mistake in the caption and add a final sentence to explain what would happen in a point neuron: all the voltage responses (clustered or scattered) would be equal.

*P. 7*

*Proof: there are two different fonts for Theta*

Thank you for alerting us to this issue, we will watch out for it in the revision proof.

*I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.*

We agree and have removed the paragraph.

*P. 8*

*Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?*

Yes, an “active synapse” receives 25 spikes over 250ms (i.e. a 100Hz input) and “inactive synapses” do not receive any spikes. We now point this out in the Figure caption and changed the text to make it clearer.

*“We think that the extension we chose is a reasonable one” Why? Please explain*

We have removed this sentence and instead now include a sentence describing the features of the function that are preserved by extending it in the way we did.

*The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?*

We have rewritten parts of the Discussion to make it more fluent.

*Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?*

We have added a paragraph discussing the issue of plasticity to the discussion. We thank the reviewer for alerting us to a number of typos (missing ‘s’ at the end of words, missing commas, etc.) and language issues which we have corrected in the revised manuscript.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 19 Oct 2020

Sacha van Albada, Institute of Neuroscience and Medicine (INM-6), Research Centre Jülich, Germany; Institute of Zoology, University of Cologne, Germany

Approved with Reservations

https://doi.org/10.5256/f1000research.29243.r72166

This paper shows that having synaptic inputs onto separate dendrites can lower the resolution and spread of the synaptic weights necessary for performing computations. The authors illustrate this using both simple threshold units and biophysical neuron models, on the example of a particular function they call ‘dominant AND’. The work appears to be novel and correct, and is presented in a well-organized, comprehensible manner. It may have an impact not only in neuroscience but also on the implementation of artificial neural networks.

Minor

The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a minimal lower bound – some threshold functions might still require larger weights. It should thus not be presented as a general condition.

The work of Ujfalussy et al. seems relevant but is not cited.

The English can be improved in places. For instance in the 2^nd paragraph of the Introduction: “synaptic weights resolution” → “synaptic weight resolution”, “compute all ...computation” → “perform all...computations”, “they evolve...with” → “the weights depend...on”. Also in other places, reword “compute computations”.

In the same paragraph “an LTU needs integer-valued weights” is a bit misleading. Of course the weights do not need to be integer-valued, they can just be taken to be integer-valued without loss of generality. In the last sentence of that paragraph, please clarify what you mean by “means”.

“The dynamics of the gating variables...are adapted from...and omitted here for brevity”: Please clarify if the dynamics are taken to be identical to the dynamics in that reference (“adapted” suggests otherwise – in which case more details would be needed for completeness).

In Definition 2, I would write “at least one vector” instead of “at least a vector”.

In Definition 5, maybe instead of “n inputs” you want to write “n inputs onto each dendrite”, and in the sum over w_{i,j} indicate the limits of j (presumably 1 to n). “d dendritic threshold” → “d dendritic thresholds”. In the first equation of Def. 5, you use limits 0 and d, and 0 and n, corresponding to (d+1) * (n+1) weights, instead of d * n, so I suggest adjusting the limits. In the second equation of Def. 5, you use X on the left-hand side but Y on the right-hand side.

“provided a sufficient number of dendrites and synapses” → “given a sufficient number of dendrites and synapses”

“It allows to...” → “This allows one to...” or “This allows us to...”
In the same sentence, please clarify what you mean by “similar synapses”.

Fig. 1 caption “compare to the others” → “compared to the others”

“the other three computations which treat” → “the other three computations, which treat”

p. 6, top: The link between focusing on D-AND and the focus on sublinearity is unclear.

Fig. 4 caption: ‘coloured squares depicts’ → ‘coloured squares depict’

p. 7, top: ‘greater or equal than’ → ‘greater than or equal to’

p. 7: ‘If one would only measure’ → ‘If one only measured’

p. 8: ‘it has now active’ → ‘it now has active’

Please be clearer on the role of the active sodium channels in supporting the computation. The abstract speaks of passive dendrites.

I would reword ‘the neuron does not overly fire notably’ to something like ‘the output firing rate remains moderate’.

Discussion: ‘many times higher than the other’ → ‘many times higher than the lowest of the other weights’ or similar

‘one of its possible extension’ → ‘one of its possible extensions’

The sentence ‘In conclusion, dendrites...than without’ is not grammatically correct.

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: computational neuroscience

CITE

Report a concern

Author Response 22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

22 Jan 2021

Author Response

The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a ... Continue reading The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a minimal lower bound – some threshold functions might still require larger weights. It should thus not be presented as a general condition.

We rewrote this part of the introduction in less technical term while improving its accuracy.

The work of Ujfalussy et al. seems relevant but is not cited.

We now cite a work their work in the introduction

The dynamics of the gating variables...are adapted from...and omitted here for brevity”: Please clarify if the dynamics are taken to be identical to the dynamics in that reference (“adapted” suggests otherwise – in which case more details would be needed for completeness).

We changed adapted to “identical, except for…”, detailing the one difference to the parameters used in the reference.

In Definition 2, I would write “at least one vector” instead of “at least a vector”. In Definition 5, maybe instead of “n inputs” you want to write “n inputs onto each dendrite”, and in the sum over w_{i,j} indicate the limits of j (presumably 1 to n). “d dendritic threshold” → “d dendritic thresholds”. In the first equation of Def. 5, you use limits 0 and d, and 0 and n, corresponding to (d+1) * (n+1) weights, instead of d * n, so I suggest adjusting the limits.

We implemented the changes and corrected our definition and kept these changes throughout the article.

In the second equation of Def. 5, you use X on the left-hand side but Y on the right-hand side.

These mistakes happened during the editorial process, we corrected them.

Pp. 6, top: The link between focusing on D-AND and the focus on sublinearity is unclear.

We upgraded figure two and three, and changed the text to make this link clearer.

Finally, we corrected all the English mistakes underlined by the reviewer, clarified it, reworded the article to avoid compute/computation and we clarified what we meant by "means".
The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a minimal lower bound – some threshold functions might still require larger weights. It should thus not be presented as a general condition.

We rewrote this part of the introduction in less technical term while improving its accuracy.

The work of Ujfalussy et al. seems relevant but is not cited.

We now cite a work their work in the introduction

The dynamics of the gating variables...are adapted from...and omitted here for brevity”: Please clarify if the dynamics are taken to be identical to the dynamics in that reference (“adapted” suggests otherwise – in which case more details would be needed for completeness).

We changed adapted to “identical, except for…”, detailing the one difference to the parameters used in the reference.

In Definition 2, I would write “at least one vector” instead of “at least a vector”. In Definition 5, maybe instead of “n inputs” you want to write “n inputs onto each dendrite”, and in the sum over w_{i,j} indicate the limits of j (presumably 1 to n). “d dendritic threshold” → “d dendritic thresholds”. In the first equation of Def. 5, you use limits 0 and d, and 0 and n, corresponding to (d+1) * (n+1) weights, instead of d * n, so I suggest adjusting the limits.

We implemented the changes and corrected our definition and kept these changes throughout the article.

In the second equation of Def. 5, you use X on the left-hand side but Y on the right-hand side.

These mistakes happened during the editorial process, we corrected them.

Pp. 6, top: The link between focusing on D-AND and the focus on sublinearity is unclear.

We upgraded figure two and three, and changed the text to make this link clearer.

Finally, we corrected all the English mistakes underlined by the reviewer, clarified it, reworded the article to avoid compute/computation and we clarified what we meant by "means".
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

22 Jan 2021

Author Response

The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a ... Continue reading The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a minimal lower bound – some threshold functions might still require larger weights. It should thus not be presented as a general condition.

We rewrote this part of the introduction in less technical term while improving its accuracy.

The work of Ujfalussy et al. seems relevant but is not cited.

We now cite a work their work in the introduction

The dynamics of the gating variables...are adapted from...and omitted here for brevity”: Please clarify if the dynamics are taken to be identical to the dynamics in that reference (“adapted” suggests otherwise – in which case more details would be needed for completeness).

We changed adapted to “identical, except for…”, detailing the one difference to the parameters used in the reference.

In Definition 2, I would write “at least one vector” instead of “at least a vector”. In Definition 5, maybe instead of “n inputs” you want to write “n inputs onto each dendrite”, and in the sum over w_{i,j} indicate the limits of j (presumably 1 to n). “d dendritic threshold” → “d dendritic thresholds”. In the first equation of Def. 5, you use limits 0 and d, and 0 and n, corresponding to (d+1) * (n+1) weights, instead of d * n, so I suggest adjusting the limits.

We implemented the changes and corrected our definition and kept these changes throughout the article.

In the second equation of Def. 5, you use X on the left-hand side but Y on the right-hand side.

These mistakes happened during the editorial process, we corrected them.

Pp. 6, top: The link between focusing on D-AND and the focus on sublinearity is unclear.

We upgraded figure two and three, and changed the text to make this link clearer.

Finally, we corrected all the English mistakes underlined by the reviewer, clarified it, reworded the article to avoid compute/computation and we clarified what we meant by "means".
The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a minimal lower bound – some threshold functions might still require larger weights. It should thus not be presented as a general condition.

We rewrote this part of the introduction in less technical term while improving its accuracy.

The work of Ujfalussy et al. seems relevant but is not cited.

We now cite a work their work in the introduction

The dynamics of the gating variables...are adapted from...and omitted here for brevity”: Please clarify if the dynamics are taken to be identical to the dynamics in that reference (“adapted” suggests otherwise – in which case more details would be needed for completeness).

We changed adapted to “identical, except for…”, detailing the one difference to the parameters used in the reference.

In Definition 2, I would write “at least one vector” instead of “at least a vector”. In Definition 5, maybe instead of “n inputs” you want to write “n inputs onto each dendrite”, and in the sum over w_{i,j} indicate the limits of j (presumably 1 to n). “d dendritic threshold” → “d dendritic thresholds”. In the first equation of Def. 5, you use limits 0 and d, and 0 and n, corresponding to (d+1) * (n+1) weights, instead of d * n, so I suggest adjusting the limits.

We implemented the changes and corrected our definition and kept these changes throughout the article.

In the second equation of Def. 5, you use X on the left-hand side but Y on the right-hand side.

These mistakes happened during the editorial process, we corrected them.

Pp. 6, top: The link between focusing on D-AND and the focus on sublinearity is unclear.

We upgraded figure two and three, and changed the text to make this link clearer.

Finally, we corrected all the English mistakes underlined by the reviewer, clarified it, reworded the article to avoid compute/computation and we clarified what we meant by "means".
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 3

VERSION 3 PUBLISHED 28 Sep 2020

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3
Version 3 (revision) 18 Apr 21		read
Version 2 (revision) 20 Jan 21	read	read	read
Version 1 28 Sep 20	read	read	read

Sacha van Albada, Institute of Neuroscience and Medicine (INM-6), Research Centre Jülich, Germany; Institute of Zoology, University of Cologne, Germany
Fleur Zeldenrust, Radboud University, Nijmegen, The Netherlands
Alexandra Tzilivaki, Foundation for Research & Technology - Hellas, Heraklion, Greece

Panayiota Poirazi, Foundation for Research & Technology - Hellas, Heraklion, Greece

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

10 Views

20 Apr 2021 | for Version 3

Fleur Zeldenrust, Department of Neurophysiology, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, The Netherlands

10 Views Cite this report Responses(0)

Approved

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational neuroscience

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

8 Views

10 Mar 2021 | for Version 2

Sacha van Albada, Institute of Neuroscience and Medicine (INM-6), Research Centre Jülich, Germany; Institute of Zoology, University of Cologne, Germany

8 Views Cite this report Responses(1)

Approved

I am happy with the changes and have no more comments on the content.

I only still have a few tiny corrections:

p. 3 “where most of the synapses lay” → “where most of the synapses lie”

p. 6 “lays alone on a dendrite” → “lies alone on a dendrite”

In Definition 5, the lower limits i=0 and j=0 should be i=1 and j=1.

p. 8 “enable to robustly” → “enable one to robustly”

p. 8, bottom: STLU → SLTU

p. 9 “allow to more efficiently” → “allow one to more efficiently”

Last sentence: “Dendrites enables” → “Dendrites enable”

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

computational neuroscience

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Back to all reports

Reviewer Report

11 Views

29 Jan 2021 | for Version 2

Fleur Zeldenrust, Department of Neurophysiology, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, The Netherlands

11 Views Cite this report Responses(1)

Approved

In the present work, we oppose the linear threshold unit (LTU) to the sub-linear threshold unit (SLTU),— I don’t think you ‘oppose’ the LTU, you rather extend it.
Remove ‘the’ before non-linear processing
I appreciate the use of ‘heterogeneity’, but I think the term ‘synaptic heterogeneity’ needs to be defined — this term is used for the first time in the discussion as such, and needs a bit explanation here. Also, it needs to be explained here why the growth of the heterogeneity can be considered a problem (that needs to be solved by using for instance your SLTU).
“Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.
‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!
Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.
Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational neuroscience

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Reader Comment

01 Apr 2021

Romain Cazé, CNRS UMR 8520, IEMN, Villeneuve d'ascq, 59650, France

We made fig.4 and fig.5 and hope that they are now self-explanatory and we emphasise the link between these two figures.

Discussion:

We specified the meaning of synaptic heterogeneity: for instance the number of binary synapse an input needs to make, it might also be the number of synaptic states or the raw number of synapses.

> “Our findings are in line with a previous study that demonstrated that SLTUs enable to robustly implement a computation22. In that study, an SLTU with eight dendrites implements direction selectivity while being resilient to massive synaptic failure. As in the present work, findings were reproduced in a biophysical model.” Of the first sentence, the grammar is incorrect. Also, I don’t get the point. Now it reads as if the two studies are in line, because they were both reproduced in a biophysical model, but somehow I doubt that that was the point that you wanted to make.

We corrected the paragraph to make the parallel between the two studies clearer

> ‘Several properties….fit with experimental observations’— could you please point to where these properties were used in your story? Especially the first: isn’t the main point of [18] that this is the case despite the synapses being at different distances from the soma? Did you use that too? That wasn’t clear from the methods/results. The second point: now this is not any longer in figure 4, it is not clear how this relates to your model!

We rewrote the paragraph to make the first and the last point clearer than before and we removed the superfluous point.

> Could you please explain how ‘synaptic rewiring’ could help neurons learn to implement for instance a D-AND, and how it differs from Hebbian learning? What do you mean exactly by rewiring, and when/how does this happen? I don’t need a whole review, but 2/3 sentences about how this could work would be nice.

We precised how a SLTU friendly learning algorithm would differ from a classic Hebbian learning algorithm.

> Finally, you mention efficiency in both the introduction and the discussion. However, there is no efficiency calculation in your results. From my perspective, more efficiency means that you can do a computation with reduced cost. So which costs are reduced by using dendrites? Could you explain?

We now insist on this point by providing a concrete example: To implement the D-AND when n=1001 a SLTU needs a single synaptic contact for the dominant input while a LTU requires a thousand.

We want to thank again the reviewer: her question and remarks made our article clearer.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

15 Views

29 Jan 2021 | for Version 2

Alexandra Tzilivaki, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

Panayiota Poirazi, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

15 Views Cite this report Responses(1)

Approved

The authors have successfully addressed all the previous comments and questions.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

computational neuroscience, dendrites

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Back to all reports

Reviewer Report

31 Views

27 Oct 2020 | for Version 1

Alexandra Tzilivaki, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

Panayiota Poirazi, Institute of Molecular Biology & Biotechnology, Foundation for Research & Technology - Hellas, Heraklion, Greece

31 Views Cite this report Responses(1)

Approved With Reservations

The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).
What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".
The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

computational neuroscience, dendrites

Respond to this report

Responses (1)

Author Response

22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

*The authors should test/report the robustness of their results by performing a sensitivity analysis for specific parameters of the model. For example, they could vary the number of dendrites, apply small changes in capacitance (Cm).*

The results we present do not depend on model details, the only mandatory feature is the sub-linear summation in the dendrite. To further emphasize this point, we have added an exploration of the synaptic weight parameter in Fig.4 and discuss how it shows the robustness of the approach. Also note that the simulation code we provide can reproduce the basic results with a simple integrate-and-fire neuron model, further showing the robustness of the results.

*What would be effect of using negative synaptic weights in the LTU vs. the "dendritic neuron".*

In general, introducing negative weights will require the weights of other synapses to be higher in order to compensate. Be aware that the D-AND function cannot be implemented (neither in the LTU nor in the SLTU) if one of the inputs only connects with a single synapse that has a negative weight. This is because for each input, there is at least one configuration of the other inputs where switching that specific input from 0 to 1 needs to switch the output result from 0 to 1. If it only connects with a negative weight, this is not possible.

*The term "dendritic neuron" is not ideal as it resembles dendritic cells, which are cells in the immune system. I would propose the use of a different term, e.g. "Neuronal dendrites" or "Neurons with dendrites".*

We have changed the title to “Neurons with dendrites” to avoid any possible confusion.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

37 Views

23 Oct 2020 | for Version 1

Fleur Zeldenrust, Department of Neurophysiology, Donders Institute for Brain, Cognition and Behaviour, Radboud University, Nijmegen, The Netherlands

37 Views Cite this report Responses(1)

Approved With Reservations

This paper shows, by fundamental derivation and simulations, that a certain class of neural computations can be more efficiently and realistically be implemented by neurons with dendrites than without dendrites. This is relevant and timely, as there has recently been an increased interest in dendritic computation, both from neuroscience and from neuromorphic computing. It is also a logical follow-up of the first author’s previous work, as mentioned in the discussion. I really appreciate the way of abstracting the neural computations to Boolean functions, as they also did in their previous work, which makes the work fundamental and generally applicable. The general setup of the paper is clear and appropriate, and the derivations and simulations are done correctly and clearly. My main comments are minor and concern the presentation, concerning the language, some further explanations and a few citations. I will add them in detail below. Overall, if these minor edits are addressed I wholeheartedly recommend this paper.

Detailed comments:

P. 3

“a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?
The formula you give for integer-valued weights does not give integer values? And n is not defined.
The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.
“Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’
“Dendrites are the receptive elementS of neurons where most of the receiving synapses lay.”
“They enable neurons to compute linearly inseparable computationS”
“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.
“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.
“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’
“and connect to the soma at their extremity” at ONE extremity.
Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)
Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

P. 4

“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.
“peculiarities” replace with something like ‘the specific implementation’
Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.
Definition 5: there are a few things unclear to me:
- θ is defined but not used. Shouldn’t that be in the definition of E?
- If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?
- Y is not defined
- I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper
“computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?
“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?

P. 5

“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before
“Here we always use” add comma between here and we
Do not start a paragraph with ‘Then’. Also, ‘Next’ might be better
“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?
“Here, the dominance of X0 is only expressed by its placement.” Please explain more
Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’

P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.
Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’
Figure 4
- These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?
- “…Membrane voltage traces responding…” a voltage trace does not respond.
- “…locations (dendrite …” -> “ locations (at the dendrite…”
- The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?
- It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites
Figure 5
- Legend: part explaining the top should not be bold.
- Top (activity of the inputs): for what input it this? 111?
- It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

P. 7

Proof: there are two different fonts for Theta
I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.
Merge paragraphs (i.e. delete white line) ending with ‘…sublinear summation.’, ‘…at the soma.’ and ‘…response.’.
Replace ; with , after individually.
Add ‘-‘ with back propagation, or make one word.

P. 8

Merge paragraphs (i.e. delete white line) ending with ‘…spike interpretation.’
Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?
Merge paragraphs (i.e. delete white line) ending with ‘…remain equal.’
“The first two Results sections look at a computation and one of its possible extension”-> “In the first two sections in the Results we describe an example of a computation and one of its possible extentionS “ (a section does not look)
“We think that the extension we chose is a reasonable one” Why? Please explain
“Note also that…” do not start a paragraph that way.
“Our study also relateS…”
The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?
Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational neuroscience

Respond to this report

Responses (1)

Author Response

22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

We thank the reviewer for the thorough review and the constructive comments. We think we have addressed all the issues that have been raised, please find a detailed point-by-point reply below (original reviewer comments in italics):

*a sufficiently large network of LTUs can approximate all possible computations” I think it depends a bit on the structure etc whether this is true (see https://en.wikipedia.org/wiki/Universal_approximation_theorem). Anyway, could there be a citation to how exactly this is meant?*

We decided not to go into details about the structure of such networks and therefore used "sufficiently large" to both encompass width and depth of the network. We now cite the study by G. Cybenko which (to our knowledge) is one of the first demonstrations of the finding.

*The formula you give for integer-valued weights does not give integer values? And n is not defined.*

We have decided to no longer give the full formula, since its details are not relevant to our study (the formula could indeed give non-integer values, but it only established a lower bound). We now only state that the Hastad et al. “studied a computation implementable by an LTU only if its synaptic weight resolution grows exponentially with the number of inputs.”

*The use of ‘means’ (in ‘finite means’) is a bit confusing: I think you mean something like ‘resources’, but you can also read it as ‘averages’.*

We have removed the consufing use of the word ‘means’ and replaced it by ‘resources’.

*Neuromorphic chips illustrate the problem and synapses often occupy the majority of the space, up to ten times more than the space occupied by neurons themselves” – I don’t really understand this sentence. How to these chips illustrate the problem? I also find the ‘and’ not logical, how does this belong together? I also miss a bit a conclusion, a ‘so…..’*

We rewrote the paragraph to clarify our point (a large number of resources in LTU-based neuromorphic chips have to be dedicated to synapses).

*“First, we investigate the three input variable computations implementable by an LTU”. I miss a sentence before this (something like: “We address this question by looking at…”). Also, what does ‘the three computations’ refer to? Which three computations? If there are only three, please include a reference or an explanation.*

We have rewritten the paragraph to make it clearer. The “three input variable computations” did not refer to three computations, but to computations of three input variables. We have rephrased this as “computations of three input variables” to avoid confusion.

*“Third, we implement this computation at a smaller cost in..” Please define cost, otherwise it is meaningless.*

We have precise this point by stating that the implementation uses “fewer synapses”.

*“This work not only shows the usefulness…” – better something like ‘a possible role’ or ‘a possible function’*

We have changed this sentence to state that the work “proposes a new role”.

“and connect to the soma at their extremity” at ONE extremity.

We have change the sentence accordingly.

    Merge paragraphs (i.e. delete white line) after eq. 2 (…compartments)

    Merge paragraphs (i.e. delete white line) after eq. 4 (… brevity)

We have merged the paragraphs and slightly changed the text surrounding the equations.

P. 4

*“the code can also be run with a simpler leaky integrate-and-fire model.” Is that code included at the repository? If yes, say so explicitly, if not, delete this sentence.*

Yes, The code in the repo can run both models. We have changed the text to make this point clearer.

* “peculiarities” replace with something like ‘the specific implementation’*

We have changed the text accordingly

* Definition 4: X ≥Z: what does this mean for vectors? The norm? Please specify.*

One vector is superior to another if all of its component are superior. This is specified as part of the definition (“meaning that for all i…”)

*Definition 5: there are a few things unclear to me:
        θ is defined but not used. Shouldn’t that be in the definition of E?*

Thank you for pointing this out. The θ was indeed meant to be the threshold in the function E, but for our purposes a fixed value of 1 is enough. We have therefore removed θ from the definition.

*If the sum of w over j (wi) and all weights are either 0 or 1, then as soon as one synapse Xj with a weight wij is 1, E is 1, is that correct?*

This is correct and we now mention this in the text.

*Y is not defined*

This was a printing error, Y is the argument of the function E (instead of X). We have corrected this.


* I don’t see the sublinear summation here, can it be explained how this is sublinear summation? Also, a figure explaining this would really help, as it is one of the core definitions of the paper*

The summation is sublinear due to the saturation of the function E, which is the simplest (and strongest) sublinear summation: E(1) = 1, but E(1 + 1) = E(1 + 1 + …) = 1 as well. The shape of the function is now more clearly depicted in Figures 2 and 3.

* “computations that cannot be implemented in an LTU without using different strictly positive synaptic weights” ‘different’ is a bit confusing here (different from what?). Maybe ‘heterogeneous’?*

We have rewritten this paragraph to make it clearer and now use ‘heterogeneous’ instead of ‘different’.


*“We list all such computations in Table 2.” “Table 2. The five computations for n = 3 inputs”. I am a bit confused: do you mean all possible computations? How? I can fill in a random combination in that truth table, and then I have a computation you have not listed yet. So what do you mean? Could you explain this (or give a reference)?*

The table only lists positive threshold functions (or, equivalently, functions implementable by an LTU with non-negative weights), not all random combinations have this property. We have explained this more clearly in the rewritten paragraph.

*P. 5*

*“An LTU (Figure 1) implements the computation” which computation does this refer to? Because you describe DOR and DAND before*

Our statement refers to both computations, we have rewritten the sentence to make this explicit.

*“sub-linear summation can be observed in completely passive dendrites due to the intrinsic saturation of synaptic conductance” Isn’t this just an effect of the driving force, as also mentioned later in the results?*

Yes, we have changed the sentence to refer to the driving force here as well.

*“Here, the dominance of X0 is only expressed by its placement.” Please explain more*

We have expanded the explanation of the mechanisms used by the SLTU vs. the LTU.

*Figure 2B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to the definition of the function E in Def. 5.

*P. 6

“…dendrites both integrate inputs sub-linearly in a given range. Therefore, we will focus on D-AND in the following section…” I don’t understand how the choice for D-AND follows from sublinear integration in dendrites.*

We agree that this sentence was confusing and have removed it.

*Figure 3B: please refer to an equation or other explicit definition of the ‘saturating functions’*

We now refer to Def. 5 in the caption.

*Figure 4
These EPSPs are huge! I understand why this is needed here (to get to the saturation), but it is not very biologically realistic. Could this be addressed in the discussion?*

These EPSPs were measured in the dendrite. When they are measured in the soma they are around 10mV and therefore more biologically realistic. While our reorganized Figure 4 no longer shows the EPSP measured at the dendrite, we now mention this point in the discussion.

*The locations of the arrows does not seem to quite correspond with the locations of measurements? At least the leftmost one should at the same position as the synapses (according to the text), not more towards the end of the dendrite, and I think the rightmost should be in the middle of the soma?*

In our reorganized figure, the arrows are no longer needed.

*It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites*

The reorganized Figure 4 now shows linear summation (i.e., without saturation) as a gray dotted line.

    Figure 5
        Legend: part explaining the top should not be bold.

        Top (activity of the inputs): for what input it this? 111?

        It would be nice if an example could be included to show that dendrites are needed, i.e. that it does not work without (saturating) dendrites

We corrected the mistake in the caption and add a final sentence to explain what would happen in a point neuron: all the voltage responses (clustered or scattered) would be equal.

*P. 7*

*Proof: there are two different fonts for Theta*

Thank you for alerting us to this issue, we will watch out for it in the revision proof.

*I’m not wild about the predator-prey analogy. I understand that you want a ‘real-world example’, but I think this one does not really apply, as something could not possibly be green and blue at the same time (and one would actually require some kind of mutual inhibition because of that). So I think this analogy only gives unnecessary confusion.*

We agree and have removed the paragraph.

*P. 8*

*Explanation Figure 5: so how is a synapse activated? Also not clear from figure. Is it silent if it is not activated, and fires with 100 Hz if it is activated?*

Yes, an “active synapse” receives 25 spikes over 250ms (i.e. a 100Hz input) and “inactive synapses” do not receive any spikes. We now point this out in the Figure caption and changed the text to make it clearer.

*“We think that the extension we chose is a reasonable one” Why? Please explain*

We have removed this sentence and instead now include a sentence describing the features of the function that are preserved by extending it in the way we did.

*The discussion reads at the moment a bit more like a collection of loose arguments than as a single section. Could it be rewritten a bit so it is a bit more of a fluent story?*

We have rewritten parts of the Discussion to make it more fluent.

*Another discussion point that needs to be addressed in the discussion is plasticity and learning: whereas synaptic plasticity mechanisms that increase or decrease the synaptic weights are well known, plasticity mechanisms that change the locations of synapses much less, to my knowledge. So what would learning in such a system look like?*

We have added a paragraph discussing the issue of plasticity to the discussion. We thank the reviewer for alerting us to a number of typos (missing ‘s’ at the end of words, missing commas, etc.) and language issues which we have corrected in the revised manuscript.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

49 Views

19 Oct 2020 | for Version 1

Sacha van Albada, Institute of Neuroscience and Medicine (INM-6), Research Centre Jülich, Germany; Institute of Zoology, University of Cologne, Germany

49 Views Cite this report Responses(1)

Approved With Reservations

Is the work clearly and accurately presented and does it cite the current literature?

Yes
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Yes
If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

computational neuroscience

Respond to this report

Responses (1)

Author Response

22 Jan 2021

Romain Cazé, IEMN, CNRS UMR 8520, Villeneuve d'asq, 59650, France

The condition on the weights given in the second paragraph of the introduction was only derived under certain conditions (n>=8 a power of 2) and it is still only a minimal lower bound – some threshold functions might still require larger weights. It should thus not be presented as a general condition.

We rewrote this part of the introduction in less technical term while improving its accuracy.

The work of Ujfalussy et al. seems relevant but is not cited.

We now cite a work their work in the introduction

The dynamics of the gating variables...are adapted from...and omitted here for brevity”: Please clarify if the dynamics are taken to be identical to the dynamics in that reference (“adapted” suggests otherwise – in which case more details would be needed for completeness).

We changed adapted to “identical, except for…”, detailing the one difference to the parameters used in the reference.

In Definition 2, I would write “at least one vector” instead of “at least a vector”. In Definition 5, maybe instead of “n inputs” you want to write “n inputs onto each dendrite”, and in the sum over w_{i,j} indicate the limits of j (presumably 1 to n). “d dendritic threshold” → “d dendritic thresholds”. In the first equation of Def. 5, you use limits 0 and d, and 0 and n, corresponding to (d+1) * (n+1) weights, instead of d * n, so I suggest adjusting the limits.

We implemented the changes and corrected our definition and kept these changes throughout the article.

In the second equation of Def. 5, you use X on the left-hand side but Y on the right-hand side.

These mistakes happened during the editorial process, we corrected them.

Pp. 6, top: The link between focusing on D-AND and the focus on sublinearity is unclear.

We upgraded figure two and three, and changed the text to make this link clearer.

Finally, we corrected all the English mistakes underlined by the reviewer, clarified it, reworded the article to avoid compute/computation and we clarified what we meant by "means".

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. McCulloch WS, Pitts W: A logical calculus of the ideas immanent in nervous activity. 1943. Bull Math Biol. 1990; 52(1–2): 99–115; discussion 73–97. PubMed Abstract | Publisher Full Text

[2] 2. Minsky M, Papert SA: Perceptrons: an introduction to computational geometry. MIT Press, Cambridge Mass, 1957.

[3] 3. Cybenko G: Approximation by superpositions of a sigmoidal function. Math Control Signal Systems. 1989; 2(4): 303–314. Publisher Full Text

[4] 4. Håstad J: On the Size of Weights for Threshold Gates. SIAM J Discrete Math. 1994; 7(3): 484–492. Publisher Full Text

[5] 5. Muroga S: Threshold logic and its applications. Wiley-Interscience, New York, 1971. Reference Source

[6] 6. Pfeil T, Potjans TC, Schrader S, et al.: Is a 4-Bit Synaptic Weight Resolution Enough? Constraints on Enabling Spike-Timing Dependent Plasticity in Neuromorphic Hardware. Front Neurosci. 2012; 6: 90. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Poirazi P, Brannon T, Mel BW: Pyramidal Neuron as Two-Layer Neural Network. Neuron. 2003; 37(6): 989–999. PubMed Abstract | Publisher Full Text

[8] 8. Tzilivaki A, Kastellakis G, Poirazi P: Challenging the point neuron dogma: FS basket cells as 2-stage nonlinear integrators. Nat Commun. 2019; 10(1): 3664. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Abrahamsson T, Cathala L, Matsui K, et al.: Thin Dendrites of Cerebellar Interneurons Confer Sublinear Synaptic Integration and a Gradient of Short-Term Plasticity. Neuron. 2012; 73(6): 1159–1172. PubMed Abstract | Publisher Full Text

[10] 10. Polsky A, Mel BW, Schiller J: Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci. 2004; 7(6): 621–7. PubMed Abstract | Publisher Full Text

[11] 11. Cazé RD, Humphries MD, Gutkin B: Spiking and saturating dendrites differentially expand single neuron computation capacity. NIPS. 2012; 1070–1078. Reference Source

[12] 12. Gidon A, Zolnik TA, Fidzinski P, et al.: Dendritic action potentials and computation in human layer 2/3 cortical neurons. Science. 2020; 367(6473): 83–87. PubMed Abstract | Publisher Full Text

[13] 13. Ujfalussy BB, Makara JK, Branco T, et al.: Dendritic nonlinearities are tuned for efficient spike-based computations in cortical circuits. eLife. eLife Sciences Publications, Ltd. 2015; 4: e10056. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Traub RD, Miles R: Neuronal Networks of the Hippocampus. Cambridge University Press, May 1991. Publisher Full Text

[15] 15. Stimberg M, Brette R, Goodman DFM: Brian 2, an intuitive and efficient neural simulator. eLife. 2019; 8: e47314. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Cazé RD, Stimberg M: Source code for publication "Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights" (Version 2020.12). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.4315011

[17] 17. Koch C, Segev I: The role of single neurons in information processing. Nat Neurosci. 2000; 3 Suppl: 1171–1177. PubMed Abstract | Publisher Full Text

[18] 18. Magee JC, Cook EP: Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nat Neurosci. 2000; 3(9): 895–903. PubMed Abstract | Publisher Full Text

[19] 19. Behabadi BF, Mel BW: Mechanisms underlying subunit independence in pyramidal neuron dendrites. Proc Natl Acad Sci U S A. 2014; 111(1): 498–503. PubMed Abstract | Publisher Full Text | Free Full Text

[20] 20. Sherman SM, Guillery RW: On the actions that one nerve cell can have on another: distinguishing “drivers” from “modulators”. Proc Natl Acad Sci U S A. 1998; 95(12): 7121–7126. PubMed Abstract | Publisher Full Text | Free Full Text

[21] 21. Hubel DH, Wiesel TN: Receptive fields and functional architecture in two nonstriate visual areas (18 and 19) of the cat. J Neurophysiol. 1965; 28(2): 229–289. PubMed Abstract | Publisher Full Text

[22] 22. Cazé RD, Jarvis S, Foust AJ, et al.: Dendrites Enable a Robust Mechanism for neuronal stimulus selectivity. Neural Comput. 2017; 29(9): 2511–2527. PubMed Abstract | Publisher Full Text

[23] 23. Fu M, Yu X, Lu J, et al.: Repetitive motor learning induces coordinated formation of clustered dendritic spines in vivo. Nature. 2012; 483(7387): 92–95. PubMed Abstract | Publisher Full Text | Free Full Text

[24] 24. Limbacher T, Legenstein R: Emergence of Stable Synaptic Clusters on Dendrites Through Synaptic Rewiring. Front Comput Neurosci. 2020; 14: 57. PubMed Abstract | Publisher Full Text | Free Full Text

[25] 25. Draghici S: On the capabilities of neural networks using limited precision weights. Neural Netw. 2002; 15(3): 395–414. PubMed Abstract | Publisher Full Text

Inputs	OR	AND/OR	AND	D-OR	D-AND
000	0	0	0	0	0
001	1	0	0	0	0
010	1	0	0	0	0
011	1	1	0	1	0
100	1	0	0	1	0
101	1	1	0	1	1
110	1	1	0	1	1
111	1	1	1	1	1

Inputs	OR	AND/OR	AND	D-OR	D-AND
000	0	0	0	0	0
001	1	0	0	0	0
010	1	0	0	0	0
011	1	1	0	1	0
100	1	0	0	1	0
101	1	1	0	1	1
110	1	1	0	1	1
111	1	1	1	1	1

Neurons with dendrites can perform linearly separable computations with low resolution synaptic weights

Abstract

Keywords

Revised Amendments from Version 2

Introduction

Methods

Biophysical neuron model

Table 1. Parameter values used in the biophysical model.

Elementary neuron model and Boolean functions

Results

Implementation of computations with three input variables

Table 2. The five classes of positive threshold functions for n = 3 inputs with their associated truth tables.

Figure 1. Minimal implementation of the Dominant AND computation (D-AND) and its dual by a linear threshold unit (LTU).

Figure 2. Minimal implementation of the Dominant AND computation (D-AND) and its dual (D-OR) by a neuron with dendrites.

Implementing the D-AND for an arbitrary number of input variables

Figure 3. Extending the D-AND implementation to n inputs.

Implementation of the D-AND in a biophysical model

Figure 4. A biophysical model sensitive to synapses’ spatial distribution.

Figure 5. A biophysical model implementing the Dominant AND (rate interpretation).

Figure 6. A biophysical model implementing the Dominant AND (spike interpretation).

Discussion

Author contributions statement

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Inputs	OR	AND/OR	AND	D-OR	D-AND
000	0	0	0	0	0
001	1	0	0	0	0
010	1	0	0	0	0
011	1	1	0	1	0
100	1	0	0	1	0
101	1	1	0	1	1
110	1	1	0	1	1
111	1	1	1	1	1