<i>iMutSig</i>: a web application to identify the most similar mutational signature using shiny

Zhi Yang; Priyatama Pandey; Paul Marjoram; Kimberly D. Siegmund

doi:10.12688/f1000research.24435.2

Home Browse iMutSig: a web application to identify the most similar mutational...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

Revised

iMutSig: a web application to identify the most similar mutational signature using shiny

[version 2; peer review: 2 approved]

Zhi Yang ¹, Priyatama Pandey¹, Paul Marjoram¹, Kimberly D. Siegmund¹

PUBLISHED 19 Nov 2020

Author details Author details

¹ Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, CA, 91003, USA

Zhi Yang
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Priyatama Pandey
Roles: Validation, Writing – Review & Editing

Paul Marjoram
Roles: Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Kimberly D. Siegmund
Roles: Funding Acquisition, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the RPackage gateway.

Abstract

There are two frameworks for characterizing mutational signatures which are commonly used to describe the nucleotide patterns that arise from mutational processes. Estimated mutational signatures from fitting these two methods in human cancer can be found online, in the Catalogue Of Somatic Mutations In Cancer (COSMIC) website or a GitHub repository. The two frameworks make differing assumptions regarding independence of base pairs and for that reason may produce different results. Consequently, there is a need to compare and contrast the results of the two methods, but no such tool currently exists. In this paper, we provide a simple and intuitive interface that allows comparisons of pairs of mutational signatures to be easily performed. Cosine similarity measures the extent of signature similarity. To compare mutational signatures of different formats, one signature type (COSMIC or pmsignature) is converted to the format of the other before the signatures are compared. iMutSig provides a simple and user-friendly web application allowing researchers to download published mutational signatures of either type and to compare signatures from COSMIC to those from pmsignature, and vice versa. Furthermore, iMutSig allows users to input a self-defined mutational signature and examine its similarity to published signatures from both data sources. iMutSig is accessible online and source code is available for download from GitHub.

Keywords

Mutational Signatures, pmsignature, COSMIC, Web interface, Shiny, R

Corresponding author: Zhi Yang

Competing interests: No competing interests were disclosed.

Grant information: This work was supported by the National Cancer Institute [P01CA196569, P30CA014089 and R21 CA226106], and the National Institute of Environmental Health Sciences [P30ES07048]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health (NIH).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2020 Yang Z et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Yang Z, Pandey P, Marjoram P and Siegmund KD. iMutSig: a web application to identify the most similar mutational signature using shiny [version 2; peer review: 2 approved]. F1000Research 2020, 9:586 (https://doi.org/10.12688/f1000research.24435.2) First published: 10 Jun 2020, 9:586 (https://doi.org/10.12688/f1000research.24435.1) Latest published: 19 Nov 2020, 9:586 (https://doi.org/10.12688/f1000research.24435.2)

Revised Amendments from Version 1

We thank the reviewers for their insightful comments. Two major changes have been made to the paper which we believe have improved it significantly.

The first change is that we updated the version of COSMIC signatures from version 3 to version 3.1, announced in June 2020 as the most recently released signatures. The other change was made based on reviewer 2’s comment on including another conversion method. Reviewer 2 suggested that we ‘collapse’ the COSMIC signature to marginal probabilities which are then multiplied together under the independence assumption before comparing the COSMIC to PM signature. We implemented the new method in the Shiny app, introduced it in the Methods section and provided new Results. Now users are able to choose either of these conversion methods (new ‘collapse’ or original ‘expand’) to identify the most similar signature of the opposite type. In addition, a new tab featuring heatmaps was implemented to provide an interactive visualization of the cosine similarity between two types of signatures. Cosine similarities are computed after converting one of the signature types to match the format of the other. In addition, we discussed the discrepancy that can arise in identifying the most similar signature of the opposite type, depending on which conversion method is selected (‘collapse’ or ‘expand’).

Based on the reviewers’ feedback, we have also made a few minor changes including 1) adding a new figure to illustrate how to convert between two types of signatures; 2) correcting the typos in the formula, text, and Shiny app user interface; 3) updating a reference and the Shiny app user interface accordingly.

See the authors' detailed response to the review by Adrian Baez-Ortega
See the authors' detailed response to the review by Vittorio Perduca

Introduction

Each human is subject to a variety of mutational processes throughout their lifetime. These processes result in a catalog of somatic mutations in the tissue creating a unique mutational profile¹. A mutational signature captures the pattern of the mutations and contexts in which those mutations occur (i.e., the neighboring bases). Examples of important mutational processes with distinct mutational signatures include aging and ultraviolet (UV) radiation. Additionally, many research groups are performing analysis to discover de novo mutational signatures in cancer^1–4.

Currently, there are two frameworks used to characterize and visualize mutational signatures^5,6. The first, proposed by Alexandrov et al., uses a vector of 96 probabilities to capture the composition of the six nucleotide substitutions (C >A, C >T, C >G, T >A, T >C, T >G) and the neighboring base immediately on each of the 5′ and 3′ side of the mutated base¹. A list of published mutational signatures can be downloaded from the Catalogue Of Somatic Mutations In Cancer (COSMIC) website⁷ (version 2, v2). Later, Alexandrov et al. published an expanded set of mutational signatures in version 3.1 (v3.1)⁸. The 72 COSMIC v3.1 Single Base Substitution (SBS) signatures include 30 v2 signatures. Based on the signature concept, but using different model assumptions, Shiraishi et al. proposed a mixed-membership model, pmsignature, which substantially reduced the number of parameters needed to characterize a signature⁹. They achieved this by assuming independence across bases, thereby reducing the number of parameters from 6*4*4-1 = 95 to (6-1)+(4-1)+(4-1) = 11⁹. The reduction in the number of parameters is greater if more flanking bases are included. However, the independence assumption might prevent signatures with dependent neighboring bases from being discovered, thereby resulting a fewer signatures. Shiraishi identified 27 signatures, all of which can be downloaded from their GitHub repository⁹. In this paper, we will refer to signatures resulting from these two methods as “COSMIC signatures” with version numbers (for those resulting from Alexandrov et al.’s method) and “PM signatures” (for those resulting from Shiraishi et al.’s method).

A large number of researchers have published scientific findings resulting from the COSMIC signature-based method^10–12, which was defined as the “gold standard" in the field by Baez-Ortega et al.⁶. Meanwhile, an increasing number of researchers are using the pmsignature-based method for samples with lower numbers of somatic variants due to it requiring fewer parameters^9,13,14. Given that both methods are widely used, investigators need the ability to compare results from their analysis with those reported in earlier databases, which may have been produced using the alternate method. For example, researchers have adopted both tools for gastric cancer and tried to compare and integrate the information from two data sources in a somewhat ad hoc manner¹⁵. No rigorous tool exists for this task. In this paper we present iMutSig, an easy-to-use tool that allows users to 1) input a new mutational signature, 2) compare it using cosine similarity to all published signatures from both the COSMIC and PM signature databases, 3) identify the most similar signatures previously reported, and 4) to assemble the information characterizing those signatures using simple point-and-click navigation.

Methods

Implementation

In order to measure the similarity between mutational signatures across two databases, we need to represent PM signatures in a way that is comparable with those from COSMIC, or represent COSMIC signatures in a way comparable to PM signatures. We call the first of these methods the “expand” method, where we expand the PM signature into a probabilistic vector with the same length as the COSMIC signature, i.e., 96. The conversion in the opposite direction, from the COSMIC signature into the PM signature format is called the “collapse” method. In the collapsed format, the PM signature is represented by a vector of 14 probabilities, the probabilities for the six possible nucleotide substitutions and the probabilities for the four possible bases at each of the two flanking base positions. In the “expand” method, to calculate each of 96 resulting probabilities in the vector, we take the constituent components that make up the COSMIC signature - which refer to the nucleotide substitution and two flanking bases at the -1 and +1 position - calculate the probability of each component for the given PM signature, and then multiply those probabilities using PM signature’s assumption of independence. For example, to calculate the probability of the COSMIC signature C[C >A]T we multiply three PM signature’s probabilities: P(C at pos -1), P(C >A), and P(T at pos +1). This example is shown in Table 1, Equation 1, and Figure 1.

Table 1. An example of PM signatures.

Nucleotide substitution
C>A	C>G	C>T	T>A	T>C	T>G
	0.003	0.879	0.003	0.090	0.014
Flanking bases
Position	A	C	G	T
-2	0.159	0.042	0.486	0.314
-1	0.044		0.870	0.034
+1	0.076	0.237	0.571
+2	0.245	0.247	0.256	0.252
Transcription strand
Plus			Minus
0.511			0.489

Figure 1. The PM signature appearing in Table 1 (top) with the ‘expanded’ signature appearing in COSMIC format (bottom).

\begin{array}{l} P (C [C > A] T) = P (C at pos - 1) P ([C > A]) P (T at pos + 1) \\ = 0.052 \times 0.012 \times 0.116 \\ = 7.24 \times 10^{- 5} \end{array} (1)

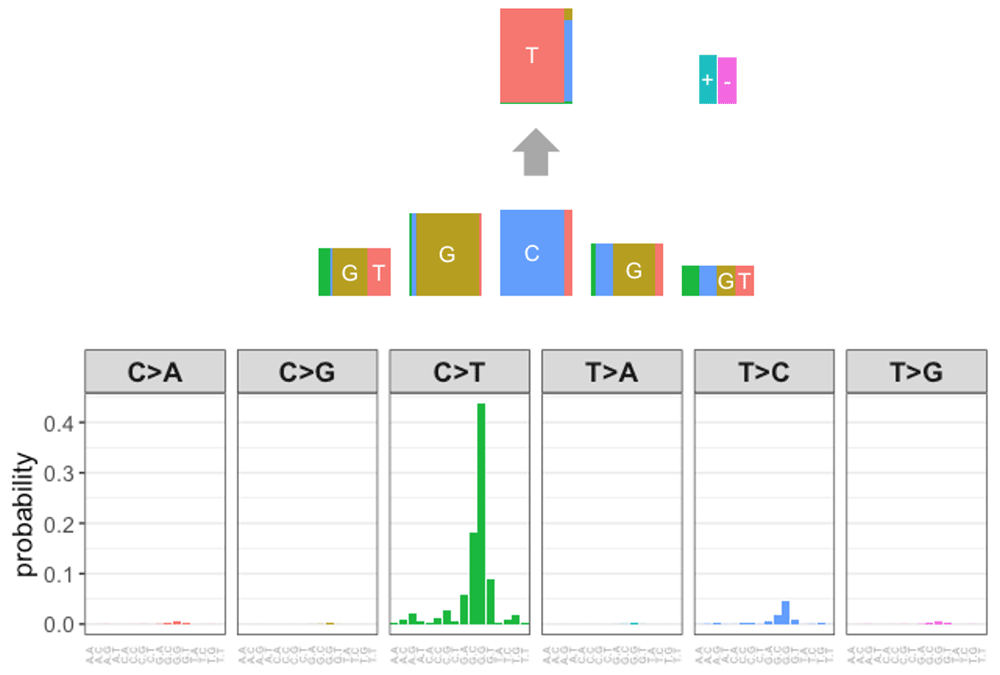
To perform the “collapse” method, we calculate the marginal probability for each characteristic, the nucleotide substitution and each flanking base, and multiply the probabilities together using the independence assumption. The marginal probability for the nucleotide substitution is computed by summing the probabilities including all 16 combinations of two flanking bases from the COSMIC signature. In a similar manner, the marginal probability of a flanking base is the sum of probabilities across all signatures containing the given flanking base. See an example of P(C>A) and P(C at pos -1) shown in Equation 2:

\begin{array}{l} P (C > A) = \sum_{i}^{A, C, G, T} \sum_{j}^{A, C, G, T} P (i [C > A] j) \\ P (C at pos - 1) = \sum_{j}^{A, C, G, T} \sum_{i}^{C > A, C > G, C > T, T > A, T > C, T > G} P (C [i] j) \end{array} (2)

These are computed using the convertAlexandrov2Shiraishi function from the decompTumor2Sig package¹⁵.

After we have represented both forms of signature using probabilistic vectors of the same length n, P and C say, we can directly compare the two signature types. In order to measure the similarity between them we use cosine similarity, CS, defined as shown in Equation 3:

C S (P, C) = \frac{P \cdot C}{‖ P ‖ \cdot ‖ C ‖} = \frac{\sum_{i = i}^{n} P_{i} \cdot C_{i}}{\sqrt{\sum_{i = 1}^{n} P_{i}^{2}} \cdot \sqrt{\sum_{i = 1}^{n} C_{i}^{2}}} (3)

Intuitively speaking, cosine similarity is the cosine of the angle between the two vectors. As such, cosine similarity ranges from 0 to 1 (inclusive). In our context, if two mutational signatures have a cosine similarity of 1, they must be identical, i.e., the angle between them is 0°; in contrast, if two mutational signatures have a cosine similarity of 0, they are maximally dissimilar (i.e., orthogonal). Computing the cosine similarity between the input signature and each of the candidate signatures, and then sorting the similarities from highest to lowest value, we identify the candidate signature with the highest cosine similarity as the most similar mutational signature.

Operation

iMutSig is built in R with its key features depending on the R package, pmsignature⁹. As shown in Figure 2, the Shiny app currently supports three possible workflows for users to choose from, depending on the type of signatures they have already obtained: 1) starting with a COSMIC signature; 2) starting with a PM signature; 3) starting with a self-defined signature that could follow either the COSMIC or PM format.

Figure 2. Overview of three workflows in the iMutSig interface.

The first two tabs allow users to finding the most similar PM signature to an input COSMIC signature (highlighted in green) and vice versa (highlighted in orange). In addition, users can identify the most similar signatures from both data sources to an input signature (highlighted in blue).

The first tab in the Shiny app window, “COSMIC to pmsignature", allows users to select an input COSMIC signature via a drop-down list and returns the best-matched PM signature. The returned results are divided and organized separately in the top and the bottom portion of the page. The top half tab summarizes background information regarding the input signature by presenting: 1) visualized plots of the input signature and its membership among all cancer types, i.e., in which kind of cancers the mutational signatures has been found; 2) a table showing the cosine similarity between this signature and all PM signatures, sorted in decreasing order, along with a visualization of a similarity heatmap with color and intensity proportional to assessed similarity. The bottom half tab presents plots and descriptions of the input COSMIC signature, the most similar PM signature, and a second PM signature that the user can select. Thus, users can easily access all the vital information and results regarding these signatures rather than having to manually gather and organize information from publications. The top half of the tab will be automatically updated via a control panel in the middle section of the tab, which enables users to select a signature to start with and also highlights information about the currently selected signature, the most-similar signature from the alternate model framework, and the cosine similarity.

The second tab was designed in a similar manner to the first tab, but for the case in which we are starting with a PM signature and looking for the most similar COSMIC signature. For the first two tabs, users can choose which version of COSMIC signatures to input from the sub-menus, i.e., v2 or v3.1.

Unlike the first two tabs, the third tab enables users to enter a user-supplied signature, which can be in either PM or COSMIC format, and then identify the most similar signature from each online database. The user will be requested to enter a sub-menu based on the type of the input signature and to upload a comma-separated values (CSV) file containing a single signature. A sample CSV file is provided for download to give the user a better sense of the format of the input file. Then, the tab will be updated to display three tables, one from each data source (COSMIC v2, v3.1 and PM), listing the signatures from that data source and the cosine similarity of each signature with the user-uploaded signature. The tables are ordered from most similar to least similar signature. In addition, the user is able to view figures of the best-matched signatures (i.e., those with highest cosine similarity) from each data source, allowing users to observe any similarities and dissimilarities. Below, users will see a list of cancer types that contain the best-matched signature.

The fourth tab shown in Figure 3 displays the interactive cosine similarity heatmaps between PM signatures and COSMIC signatures for the two conversion methods. One would choose the version of COSMIC signatures (v2 or v3.1) and one of the two conversion methods (COSMIC to PM signature, ‘collapse’, or PM signature to COSMIC, ‘expand’). The PM signature, the COSMIC signature names and the associated cosine similarity value can be visualized by placing the cursor over the heatmap. It is notable that the cosine similarity values tend to be higher using the collapse representation compared to the expand representation. We attribute this to the difference in model assumptions. When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not. This difference in model assumptions results in lower estimates of cosine similarity. Some discrepancies are found, based on the conversion method selected, when searching for the most similar signature from the opposite database: matching COSMIC v3.1 signatures to PM signatures 17 out of 72 disagreed (23.6%). A similar fraction disagreed when matching COSMIC v2 to PM signatures (7 out of 30, 23.3%). Interestingly, when we compare the 27 PM signatures to COSMIC, we see much better agreement with the newer v3.1 signatures compared to the earlier v2 signatures (88.9% vs 63%). The higher matching of the v3.1 database includes the matching of signatures that were not present in the earlier v2 database (e.g. SBS10b, SBS46, SBS49). The remaining discrepant results may correspond to COSMIC signatures that reflect dependence between neighboring bases.

Figure 3. Cosine similarity heatmaps between PM signatures and COSMIC signatures.

Use cases

We use iMutSig to identify the most similar signature for a given PM/COSMIC signature or a user-supplied signature. Figure 4 shows the input panel after inputting COSMIC v3.1 signature SBS1 and Figure 5 shows the input panel after inputting PM signature P1. If users provide a user-supplied signature of either COSMIC-kind or PM-kind, the results can be seen in Figure 6 and Figure 7. Consider the example shown in Figure 6, where we input COSMIC v2 signature C1. iMutSig returned the most similar signatures COSMIC v3.1 signature SBS1, and PM signature P7 (similarity = 0.947, and 0.948, respectively) along with the names of its associated cancer types. When providing PM signature P1, iMutSig returned COSMIC v2 signature C10, v3.1 signature C10a and PM signature P1 (similarity = 0.816, 0.957, 1.0, respectively).

Figure 4. Input a COSMIC v3.1 signature, SBS1.

Figure 5. Input a PM signature, P1.

Figure 6. Input a user-supplied COSMIC signature.

Figure 7. Input a user-supplied PM signature.

Conclusions

iMutSig is a user-friendly interactive browser-based application that allows users who have a signature that they have discovered in an analysis of their own data to identify the best-matched existing mutational signature from the COSMIC and PM databases. It also allows users to directly compare signatures between the two databases. It does this in an interactive way, and also allows straightforward visualization of results. iMutSig enables researchers to easily identify the most similar mutational signature and to easily access characteristic information from both data sources without additional software installation and programming of their own.

Data availability

All data underlying the results are available as part of the article and no additional source data are required.

Software availability

Software available from: https://zhiyang.shinyapps.io/iMutSig/

Source code available from: http://www.github.com/USCbiostats/iMutSig

Archived source code at time of publication: https://doi.org/10.5281/zenodo.4132416¹⁶

License: MIT

Faculty Opinions recommended

References

1. Alexandrov LB, Nik-Zainal S, Wedge DC, et al.: Signatures of mutational processes in human cancer. Nature. 2013; 500(7463): 415–21. PubMed Abstract | Publisher Full Text | Free Full Text
2. Yang Z, Pandey P, Shibata D, et al.: HiLDA: a statistical approach to investigate differences in mutational signatures. bioRxiv. 2019; 577452. Publisher Full Text
3. Gröschel S, Hübschmann D, Raimondi F, et al.: Defective homologous recombination DNA repair as therapeutic target in advanced chordoma. Nat Commun. 2019; 10(1): 1635. PubMed Abstract | Publisher Full Text | Free Full Text
4. Ülgen E, Can C, Bilguvar K, et al.: Whole exome sequencing–based analysis to identify DNA damage repair deficiency as a major contributor to gliomagenesis in adult diffuse gliomas. J Neurosurg. 2019; 1(aop): 1–12. PubMed Abstract | Publisher Full Text
5. Omichessan H, Severi G, Perduca V: Computational tools to detect signatures of mutational processes in DNA from tumours: a review and empirical comparison of performance. PLoS One. 2019; 14(9): e0221235. PubMed Abstract | Publisher Full Text | Free Full Text
6. Baez-Ortega A, Gori K: Computational approaches for discovery of mutational signatures in cancer. Brief Bioinform. 2017; 20(1): 77–88. PubMed Abstract | Publisher Full Text | Free Full Text
7. Forbes SA, Beare D, Boutselakis H, et al.: COSMIC: somatic cancer genetics at high-resolution. Nucleic Acids Res. 2016; 45(D1): D777–D783. PubMed Abstract | Publisher Full Text | Free Full Text
8. Alexandrov LB, Kim J, Haradhvala NJ, et al.: The repertoire of mutational signatures in human cancer. Nature. 2020; 578(7793): 94–101. PubMed Abstract | Publisher Full Text | Free Full Text
9. Shiraishi Y, Tremmel G, Miyano S, et al.: A simple model-based approach to inferring and visualizing cancer mutation signatures. PLoS Genet. 2015; 11(12): e1005657. PubMed Abstract | Publisher Full Text | Free Full Text
10. Nik-Zainal S, Loo PV, Wedge DC, et al.: The life history of 21 breast cancers. Cell. 2012; 149(5): 994–1007. PubMed Abstract | Publisher Full Text | Free Full Text
11. Schulze K, Imbeaud S, Letouzé E, et al.: Exome sequencing of hepatocellular carcinomas identifies new mutational signatures and potential therapeutic targets. Nat Genet. 2015; 47(5): 505–511. PubMed Abstract | Publisher Full Text | Free Full Text
12. Helleday T, Eshtad S, Nik-Zainal S: Mechanisms underlying mutational signatures in human cancers. Nat Rev Genet. 2014; 15(9): 585–98. PubMed Abstract | Publisher Full Text | Free Full Text
13. Yokoyama A, Kakiuchi N, Yoshizato T, et al.: Age-related remodelling of oesophageal epithelia by mutated cancer drivers. Nature. 2019; 565(7739): 312–317. PubMed Abstract | Publisher Full Text
14. Guo J, Huang J, Zhou Y, et al.: Germline and somatic variations influence the somatic mutational signatures of esophageal squamous cell carcinomas in a chinese population. BMC Genomics. 2018; 19(1): 538. PubMed Abstract | Publisher Full Text | Free Full Text
15. Krüger S, Piro RM: decompTumor2Sig: Identification of mutational signatures active in individual tumors. BMC Bioinformatics. 2019; 20(Suppl 4): 152. PubMed Abstract | Publisher Full Text | Free Full Text
16. Yang Z: USCbiostats/iMutSig v1.2 (version v1.2). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.4132416

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 10 Jun 2020

Author details Author details

¹ Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, CA, 91003, USA

Zhi Yang
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Priyatama Pandey
Roles: Validation, Writing – Review & Editing

Paul Marjoram
Roles: Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Kimberly D. Siegmund
Roles: Funding Acquisition, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This work was supported by the National Cancer Institute [P01CA196569, P30CA014089 and R21 CA226106], and the National Institute of Environmental Health Sciences [P30ES07048]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health (NIH).
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 19 Nov 2020, 9:586

https://doi.org/10.12688/f1000research.24435.2

version 1

Published: 10 Jun 2020, 9:586

https://doi.org/10.12688/f1000research.24435.1

© 2020 Yang Z et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Yang Z, Pandey P, Marjoram P and Siegmund KD. iMutSig: a web application to identify the most similar mutational signature using shiny [version 2; peer review: 2 approved]. F1000Research 2020, 9:586 (https://doi.org/10.12688/f1000research.24435.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 19 Nov 2020

Revised

Views

Reviewer Report 27 Nov 2020

Adrian Baez-Ortega, Transmissible Cancer Group, Department of Veterinary Medicine, University of Cambridge, Cambridge, UK

Approved

https://doi.org/10.5256/f1000research.30641.r75096

In this revised manuscript, Yang et al. satisfactorily address all the major and minor revisions originally requested, resulting in improvements to both the paper and the software tool. Hence I believe this paper to be scientifically sound in its present form, and no further major revisions should be necessary. However, below I add a few non-essential points that could be addressed, all of which are quite straightforward and should not require an additional round of review. Moreover, I would understand if the authors disagreed with my last comment regarding cosine similarities.

In the iMutSig app, I noticed that the panel showing the membership of the selected COSMIC signature across tumour types does not display anything for some of the v3.1 signatures (e.g. SBS27, SBS28), while it does work for their v2 counterparts (e.g. C27, C28). I do not know if this is a mistake or if the distributions of some v3.1 signatures are really unknown.
Introduction, par. 2 reads: "thereby resulting a fewer signatures" instead of "thereby resulting in fewer signatures"; and "Shiraishi identified 27 signatures" instead of "Shiraishi et al. identified 27 signatures".
In Implementation, par. 1, when discussing the "expand" method whereby a COSMIC signature is constructed from three of the probabilities in the input PM signature, perhaps it would be good to mention that the PM signature may contain more features than just substitution type and immediate 5' and 3' bases (such as probabilities for -2/+2 bases and transcriptional strand), and that any information about these extra features of the PM signature is lost when "expanding" to the COSMIC format. Adding this comment might be valuable since the example in Table 1 does contain these extra features, and it would also highlight one of the strengths of PM signatures (more information in less parameters).
Implementation, par. 1 reads: "For example, to calculate the probability of the COSMIC signature C[C >A]T...". Should it not be "the COSMIC mutation type C[C>A]T"? A COSMIC signature would be a vector of 96 such mutation types/categories.
The comment above also applies to the next paragraph, which reads: "In a similar manner, the marginal probability of a flanking base is the sum of probabilities across all signatures containing the given flanking base."
Implementation, par. 2 reads: "To perform the “collapse” method, we calculate the marginal probability for each characteristic, the nucleotide substitution and each flanking base, and multiply the probabilities together using the independence assumption". Are you sure that the probabilities are multiplied together in the "collapse" method? As far as I understand, each marginal probability is obtained as a summation (as shown in Equation 2), and no multiplication is required afterwards – if I am correct, these marginal probabilities already define the PM signature.
Figure 2 legend reads: "The first two tabs allow users to finding...", instead of "to find".
Operation, par. 5 reads: "It is notable that the cosine similarity values tend to be higher using the collapse representation compared to the expand representation. We attribute this to the difference in model assumptions. When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not." While I understand this, I am not sure this is the only reason for the difference in cosine similarities. In general, one would expect high cosine similarity values to become less frequent as the number of dimensions increases; in other words, it is much less likely to find two 96-dimensional vectors with a near-zero angle between them than it is to find two 11-dimensional vectors with a similar angle. So it is possible that the mere fact of collapsing a COSMIC signature into a PM signature causes an overall increase in its cosine similarity with every other PM signature (and the opposite would be true when "expanding" signatures). However, I do not know which of these two explanations is more important for the change in similarity values observed in the signature heatmaps.

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational biology, Bioinformatics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 26 Nov 2020

Vittorio Perduca, Université de Paris, CNRS, MAP5 UMR 8145, F-75006, Paris, France

Approved

https://doi.org/10.5256/f1000research.30641.r75097

Thank you for taking into account my comments and for clarifying the differences between ... Continue reading

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 10 Jun 2020

Views

Reviewer Report 15 Jul 2020

Vittorio Perduca, Université de Paris, CNRS, MAP5 UMR 8145, F-75006, Paris, France

Approved with Reservations

https://doi.org/10.5256/f1000research.26954.r64570

This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on one side¹, and lower dimensional "pmsignature" vectors on the other side². The article is well written and the method behind the tool is clearly explained. The interactive tool runs smoothly and has the potential to provide useful support to researchers running mutational signature analyses using alternative frameworks.

My comments:

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.
My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?
In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.
I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

References

1. Alexandrov LB, Nik-Zainal S, Wedge DC, Aparicio SA, et al.: Signatures of mutational processes in human cancer.Nature. 2013; 500 (7463): 415-21 PubMed Abstract | Publisher Full Text
2. Shiraishi Y, Tremmel G, Miyano S, Stephens M: A Simple Model-Based Approach to Inferring and Visualizing Cancer Mutation Signatures.PLoS Genet. 2015; 11 (12): e1005657 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Applied statistics, biostatistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 19 Nov 2020

Zhi Yang, Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, 91003, USA

19 Nov 2020

Author Response
This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on ... Continue reading
This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on one side¹, and lower dimensional "pmsignature" vectors on the other side². The article is well written and the method behind the tool is clearly explained. The interactive tool runs smoothly and has the potential to provide useful support to researchers running mutational signature analyses using alternative frameworks.

My comments:

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.

Response: We now summarize explicitly the tasks the software performs at the end of the introduction: “iMutSig, an easy-to-use tool that allows users to 1) input a new mutational signature, 2) compare it using Cosine similarity to all published signatures from both the COSMIC and PM-signature databases, 3) identify the most similar signatures previously reported, and 4) to assemble the information characterizing those signatures using simple point-and-click navigation.”

My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?

Response: We are not recommending one method over another, but are providing a means for comparing signatures that are estimated under the different modeling assumptions. One can transform the format of either signature type to the format used by the other signature type (PM signature to COSMIC or COSMIC to PM signature). In the original submission we only considered expanding the PM signature to the COSMIC format. In this revision we have added the capability of collapsing the COSMIC signature to the PM signature format (see response to next comment). These are not symmetric activities and can lead to differences in the identification of most similar signature from the opposite model. The new method of ‘collapsing’ the COSMIC signature is described in the section: “Methods/Implementation”. The consequences for identifying the most similar signature of the opposite type are described in the last paragraph under “Methods/Operation”.

In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.

Response: Thank you for this suggestion. As we noted in our response to your last point, we have added this additional comparison to the app using a function implemented in the decompTumor2Sig package. Interestingly, the cosine similarity values tend to be higher using the above method. We interpret this in the paper as follows: “When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not. This difference in model assumptions results in lower estimates of cosine similarity.” (section Methods/Operation).

I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Response: The heatmap is now added to the Shiny app and the manuscript.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Response: We have corrected this typo in this version of the manuscript.
This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on one side¹, and lower dimensional "pmsignature" vectors on the other side². The article is well written and the method behind the tool is clearly explained. The interactive tool runs smoothly and has the potential to provide useful support to researchers running mutational signature analyses using alternative frameworks.

My comments:

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.

Response: We now summarize explicitly the tasks the software performs at the end of the introduction: “iMutSig, an easy-to-use tool that allows users to 1) input a new mutational signature, 2) compare it using Cosine similarity to all published signatures from both the COSMIC and PM-signature databases, 3) identify the most similar signatures previously reported, and 4) to assemble the information characterizing those signatures using simple point-and-click navigation.”

My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?

Response: We are not recommending one method over another, but are providing a means for comparing signatures that are estimated under the different modeling assumptions. One can transform the format of either signature type to the format used by the other signature type (PM signature to COSMIC or COSMIC to PM signature). In the original submission we only considered expanding the PM signature to the COSMIC format. In this revision we have added the capability of collapsing the COSMIC signature to the PM signature format (see response to next comment). These are not symmetric activities and can lead to differences in the identification of most similar signature from the opposite model. The new method of ‘collapsing’ the COSMIC signature is described in the section: “Methods/Implementation”. The consequences for identifying the most similar signature of the opposite type are described in the last paragraph under “Methods/Operation”.

In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.

Response: Thank you for this suggestion. As we noted in our response to your last point, we have added this additional comparison to the app using a function implemented in the decompTumor2Sig package. Interestingly, the cosine similarity values tend to be higher using the above method. We interpret this in the paper as follows: “When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not. This difference in model assumptions results in lower estimates of cosine similarity.” (section Methods/Operation).

I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Response: The heatmap is now added to the Shiny app and the manuscript.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Response: We have corrected this typo in this version of the manuscript.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 19 Nov 2020

Zhi Yang, Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, 91003, USA

19 Nov 2020

Author Response
This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on ... Continue reading
This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on one side¹, and lower dimensional "pmsignature" vectors on the other side². The article is well written and the method behind the tool is clearly explained. The interactive tool runs smoothly and has the potential to provide useful support to researchers running mutational signature analyses using alternative frameworks.

My comments:

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.

Response: We now summarize explicitly the tasks the software performs at the end of the introduction: “iMutSig, an easy-to-use tool that allows users to 1) input a new mutational signature, 2) compare it using Cosine similarity to all published signatures from both the COSMIC and PM-signature databases, 3) identify the most similar signatures previously reported, and 4) to assemble the information characterizing those signatures using simple point-and-click navigation.”

My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?

Response: We are not recommending one method over another, but are providing a means for comparing signatures that are estimated under the different modeling assumptions. One can transform the format of either signature type to the format used by the other signature type (PM signature to COSMIC or COSMIC to PM signature). In the original submission we only considered expanding the PM signature to the COSMIC format. In this revision we have added the capability of collapsing the COSMIC signature to the PM signature format (see response to next comment). These are not symmetric activities and can lead to differences in the identification of most similar signature from the opposite model. The new method of ‘collapsing’ the COSMIC signature is described in the section: “Methods/Implementation”. The consequences for identifying the most similar signature of the opposite type are described in the last paragraph under “Methods/Operation”.

In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.

Response: Thank you for this suggestion. As we noted in our response to your last point, we have added this additional comparison to the app using a function implemented in the decompTumor2Sig package. Interestingly, the cosine similarity values tend to be higher using the above method. We interpret this in the paper as follows: “When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not. This difference in model assumptions results in lower estimates of cosine similarity.” (section Methods/Operation).

I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Response: The heatmap is now added to the Shiny app and the manuscript.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Response: We have corrected this typo in this version of the manuscript.
This paper presents an original online tool for comparing mutational signatures represented according to two alternative formats, namely COSMIC vectors with the relative frequencies of the 96 types of substitutions on one side¹, and lower dimensional "pmsignature" vectors on the other side². The article is well written and the method behind the tool is clearly explained. The interactive tool runs smoothly and has the potential to provide useful support to researchers running mutational signature analyses using alternative frameworks.

My comments:

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.

Response: We now summarize explicitly the tasks the software performs at the end of the introduction: “iMutSig, an easy-to-use tool that allows users to 1) input a new mutational signature, 2) compare it using Cosine similarity to all published signatures from both the COSMIC and PM-signature databases, 3) identify the most similar signatures previously reported, and 4) to assemble the information characterizing those signatures using simple point-and-click navigation.”

My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?

Response: We are not recommending one method over another, but are providing a means for comparing signatures that are estimated under the different modeling assumptions. One can transform the format of either signature type to the format used by the other signature type (PM signature to COSMIC or COSMIC to PM signature). In the original submission we only considered expanding the PM signature to the COSMIC format. In this revision we have added the capability of collapsing the COSMIC signature to the PM signature format (see response to next comment). These are not symmetric activities and can lead to differences in the identification of most similar signature from the opposite model. The new method of ‘collapsing’ the COSMIC signature is described in the section: “Methods/Implementation”. The consequences for identifying the most similar signature of the opposite type are described in the last paragraph under “Methods/Operation”.

In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.

Response: Thank you for this suggestion. As we noted in our response to your last point, we have added this additional comparison to the app using a function implemented in the decompTumor2Sig package. Interestingly, the cosine similarity values tend to be higher using the above method. We interpret this in the paper as follows: “When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not. This difference in model assumptions results in lower estimates of cosine similarity.” (section Methods/Operation).

I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Response: The heatmap is now added to the Shiny app and the manuscript.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Response: We have corrected this typo in this version of the manuscript.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 22 Jun 2020

Adrian Baez-Ortega, Transmissible Cancer Group, Department of Veterinary Medicine, University of Cambridge, Cambridge, UK

Approved with Reservations

https://doi.org/10.5256/f1000research.26954.r64568

Yang et al. present an interactive software tool, iMutSig, which allows comparison between two alternative mathematical representations of mutational signatures. Both of these representations are widely used, but are remarkably different in their visual aspect, making intuitive comparisons difficult. To my knowledge, this is the first openly available method for comparison between signatures expressed in these two alternative representations.

The methods implemented for conversion between signature representations and for comparison between signatures are straightforward and based on a widely used similarity measure; although the main formula in the paper is incorrect, this mistake does not appear to extend to the implementation. Instead of simply reporting the most similar signature to the chosen signature, the tool provides information about the similarity of the chosen signature to all the signatures available in the alternative representation, allowing better assessment of the results. The user interface is thoughtfully and tastefully designed, making the tool both easy and pleasant to use. All the offered functionalities appear to work correctly and the platform runs smoothly. The authors provide their tool as an interactive website, as well as current and archived versions of the source code. However, there is a lack of information about how to install and run the software locally as an R package, which would increase the long-term usability of the tool.

Below I provide comments regarding major and minor issues in the article and online tool. I also provide a few optional suggestions that may be safely ignored, but which I think would enhance the functionality of the tool.

MAJOR COMMENTS

1. Implementation, paragraph 2: The formula for the cosine similarity defined in Equation 2 is not correct. While it is true that
CS(P,C) = (P·C) / (||P||·||C||),
it is not true that
CS(P,C) = sum(P_i * C_i) / (sum(P_i) * sum(C_i)).

The correct formula for the third part of Equation 2 would be:
CS(P,C) = sum(P_i * C_i) / (sqrt(sum(P_i^2)) * sqrt(sum(C_i^2)))
(see here).

Please ammend this formula, and make sure that it gives the same values as the formula you have defined in your code (function getCosDistance).

MINOR COMMENTS

2. Introduction, paragraph 1: This is somewhat inaccurate, in the sense that it is the cells in an organism's tissues that are exposed to mutational processes throughout the organism's life, and each cell or tissue develops its own mutational profile. The existence of a "unique mutational profile" thus may be better described as a property of a tissue, organ or tumour: it is not really accurate to say that each human has "his/her unique mutational profile", as this varies widely across tissues (e.g. cells in the blood, skin, liver, and colon have very different mutational spectra), and the differences among individuals also tend to be tissue-specific.

3. Introduction, paragraph 3: in the sentence where the motivation for PM signatures is mentioned ("due to it requiring fewer parameters"), it might be appropriate to add a brief note that the assumption of independence between substitution type and flanking bases also limits the representation of patterns where these features are dependent, although this is seen in relatively few COSMIC signatures (e.g. SBS8, SBS25, SBS35).

4. Implementation, paragraph 1: it would be useful to complement the example in Table 1 and Equation 1 with a figure that shows the original PM signature in Table 1, and the equivalent COSMIC signature that results from applying Equation 1 to each of the 96 substitution types. This would help the reader to understand the conversion between both graphical representations, which is shown in later figures.

5. Note that reference 5 has an updated version: Omichessan, Severi & Perduca (2019)¹.

6. Note that reference 6 is missing a colon between the author list and title.

7. The "About iMutSig" web page states that "On the Github page, you can: - install the iMutSig R pacakge and run it locally." However, on the GitHub page I found no instructions on how the package can be installed and run locally using R and Shiny. While I understand that the main purpose of the platform is to be an online tool, some users may be interested in having a local copy. For example, the availability of the tool seemed somewhat variable: I was able to access the website (https://zhiyang.shinyapps.io/imutsig/) on 17 June, but not on 18 June. Although this might be a rare issue, it highlights the advantage of providing users with an alternative way of accessing the tool in the long term. For example, some simple steps for installation and running could be added as a README.md file on the GitHub repository.

8. Note that, in the platform interface, some of the signature names read "COSIMIC" instead of "COSMIC".

OPTIONAL SUGGESTIONS

9. I found it strange that in the tabs "COSMIC to pmsignature" and "pmsignature to COSMIC", the drop-down menus for choosing the COSMIC and PM signatures to compare are located in the middle of the interface, below the top panels that show the chosen signature. It seems to me that it would be more intuitive to place the selection menus at the top of the page, although I might be wrong.

10. The authors might consider extending the user-supplied signature mode to allow the user to input a set of signatures, and then select the signature to compare using a drop-down menu (as in the other comparison modes), as it is likely that users will be interested in analysing sets of signatures, rather than single signatures. However, I understand this might not be straightforward to implement.

11. Another potential extension could be an additional mode in which comparison could be performed between two sets of user-supplied signatures (each of which could be in COSMIC or PM format), in order to find the best one-to-one match between the signatures.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

References

1. Omichessan H, Severi G, Perduca V: Computational tools to detect signatures of mutational processes in DNA from tumours: A review and empirical comparison of performance.PLoS One. 2019; 14 (9): e0221235 PubMed Abstract | Publisher Full Text

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational biology, Bioinformatics.

CITE

Report a concern

Author Response 19 Nov 2020

Zhi Yang, Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, 91003, USA

19 Nov 2020

Author Response

We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: ... Continue reading We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: The formula for the cosine similarity defined in Equation 2 is not correct. While it is true that
CS(P,C) = (P·C) / (||P||·||C||),
it is not true that
CS(P,C) = sum(P_i * C_i) / (sum(P_i) * sum(C_i)).

The correct formula for the third part of Equation 2 would be:
CS(P,C) = sum(P_i * C_i) / (sqrt(sum(P_i^2)) * sqrt(sum(C_i^2)))
(see here).

Please amend this formula, and make sure that it gives the same values as the formula you have defined in your code (function getCosDistance).

Response: The formula has been corrected in this new version of the manuscript. We have also verified that the formula was correctly implemented in the getCosDistance function in the software (see below).

getCosDistance <- function(F_1, F_2) {

if(length(F_1)!=length(F_2)){
    geterrmessage("Two signatures have different number of bases!")
}

cos <- sum(F_1*F_2)/(sqrt(sum(F_1^2))*sqrt(sum(F_2^2)))
return(cos)
}

MINOR COMMENTS

2. Introduction, paragraph 1: This is somewhat inaccurate, in the sense that it is the cells in an organism's tissues that are exposed to mutational processes throughout the organism's life, and each cell or tissue develops its own mutational profile. The existence of a "unique mutational profile" thus may be better described as a property of a tissue, organ or tumour: it is not really accurate to say that each human has "his/her unique mutational profile", as this varies widely across tissues (e.g. cells in the blood, skin, liver, and colon have very different mutational spectra), and the differences among individuals also tend to be tissue-specific.

Response: We agree that our phrasing was poorly chosen here. We have altered the text to reflect this comment. The text now says “These processes result in a catalog of somatic mutations in the tissue creating…”.

3. Introduction, paragraph 3: in the sentence where the motivation for PM signatures is mentioned ("due to it requiring fewer parameters"), it might be appropriate to add a brief note that the assumption of independence between substitution type and flanking bases also limits the representation of patterns where these features are dependent, although this is seen in relatively few COSMIC signatures (e.g. SBS8, SBS25, SBS35).

Response: We have added a sentence addressing this disadvantage of using the independence assumption. “However, the independence assumption might prevent signatures with dependent bases from being discovered, thereby resulting in fewer signatures.”

4. Implementation, paragraph 1: it would be useful to complement the example in Table 1 and Equation 1 with a figure that shows the original PM signature in Table 1, and the equivalent COSMIC signature that results from applying Equation 1 to each of the 96 substitution types. This would help the reader to understand the conversion between both graphical representations, which is shown in later figures.

Response: : As requested, we have added a new Figure 1 that shows the signature in Table 1 and the ‘expanded’ signature in COSMIC format to help illustrate Equation 1.

5. Note that reference 5 has an updated version: Omichessan, Severi & Perduca (2019)¹.

Response: Reference 5 is now updated.

6. Note that reference 6 is missing a colon between the author list and title.

Response: : The colon has been added to reference 6.

7. The "About iMutSig" web page states that "On the GitHub page, you can: - install the iMutSig R pacakge and run it locally." However, on the GitHub page I found no instructions on how the package can be installed and run locally using R and Shiny. While I understand that the main purpose of the platform is to be an online tool, some users may be interested in having a local copy. For example, the availability of the tool seemed somewhat variable: I was able to access the website (https://zhiyang.shinyapps.io/imutsig/) on 17 June, but not on 18 June. Although this might be a rare issue, it highlights the advantage of providing users with an alternative way of accessing the tool in the long term. For example, some simple steps for installation and running could be added as a README.md file on the GitHub repository.

Response: Thank you for the suggestion. A new README.md file was added to the GitHub repository (https://github.com/USCbiostats/iMutSig) providing instructions on how to install the necessary packages and host the app locally. The website failure on June 18^th resulted from a scheduled automatic downloading procedure which exceeded the server response time. Subsequently, we found that the COSMIC website posted new versions of signatures (v3.1) under a different website, allowing us to remove the automatic download procedure and avoid such an issue in the future.

8. Note that, in the platform interface, some of the signature names read "COSIMIC" instead of "COSMIC".

Response: Those typos have been corrected.

OPTIONAL SUGGESTIONS

9. I found it strange that in the tabs "COSMIC to pmsignature" and "pmsignature to COSMIC", the drop-down menus for choosing the COSMIC and PM signatures to compare are located in the middle of the interface, below the top panels that show the chosen signature. It seems to me that it would be more intuitive to place the selection menus at the top of the page, although I might be wrong.

Response: The dropdown menu for selection is now at the top of the webpage.

10. The authors might consider extending the user-supplied signature mode to allow the user to input a set of signatures, and then select the signature to compare using a drop-down menu (as in the other comparison modes), as it is likely that users will be interested in analysing sets of signatures, rather than single signatures. However, I understand this might not be straightforward to implement.

Response: Thank you for the suggestion. Indeed, allowing multiple signature inputs will require introducing a drop-down menu in order to maintain the current layout. Although not incorporated at this time, we plan to add this feature in the future.

11. Another potential extension could be an additional mode in which comparison could be performed between two sets of user-supplied signatures (each of which could be in COSMIC or PM format), in order to find the best one-to-one match between the signatures.

Response: Thank you for this suggestion as well. In the future, we also plan to add this feature by adding a tab allowing the comparison between user-supplied signatures.
We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: The formula for the cosine similarity defined in Equation 2 is not correct. While it is true that
CS(P,C) = (P·C) / (||P||·||C||),
it is not true that
CS(P,C) = sum(P_i * C_i) / (sum(P_i) * sum(C_i)).

The correct formula for the third part of Equation 2 would be:
CS(P,C) = sum(P_i * C_i) / (sqrt(sum(P_i^2)) * sqrt(sum(C_i^2)))
(see here).

Please amend this formula, and make sure that it gives the same values as the formula you have defined in your code (function getCosDistance).

Response: The formula has been corrected in this new version of the manuscript. We have also verified that the formula was correctly implemented in the getCosDistance function in the software (see below).

getCosDistance <- function(F_1, F_2) {

if(length(F_1)!=length(F_2)){
    geterrmessage("Two signatures have different number of bases!")
}

cos <- sum(F_1*F_2)/(sqrt(sum(F_1^2))*sqrt(sum(F_2^2)))
return(cos)
}

MINOR COMMENTS

2. Introduction, paragraph 1: This is somewhat inaccurate, in the sense that it is the cells in an organism's tissues that are exposed to mutational processes throughout the organism's life, and each cell or tissue develops its own mutational profile. The existence of a "unique mutational profile" thus may be better described as a property of a tissue, organ or tumour: it is not really accurate to say that each human has "his/her unique mutational profile", as this varies widely across tissues (e.g. cells in the blood, skin, liver, and colon have very different mutational spectra), and the differences among individuals also tend to be tissue-specific.

Response: We agree that our phrasing was poorly chosen here. We have altered the text to reflect this comment. The text now says “These processes result in a catalog of somatic mutations in the tissue creating…”.

3. Introduction, paragraph 3: in the sentence where the motivation for PM signatures is mentioned ("due to it requiring fewer parameters"), it might be appropriate to add a brief note that the assumption of independence between substitution type and flanking bases also limits the representation of patterns where these features are dependent, although this is seen in relatively few COSMIC signatures (e.g. SBS8, SBS25, SBS35).

Response: We have added a sentence addressing this disadvantage of using the independence assumption. “However, the independence assumption might prevent signatures with dependent bases from being discovered, thereby resulting in fewer signatures.”

4. Implementation, paragraph 1: it would be useful to complement the example in Table 1 and Equation 1 with a figure that shows the original PM signature in Table 1, and the equivalent COSMIC signature that results from applying Equation 1 to each of the 96 substitution types. This would help the reader to understand the conversion between both graphical representations, which is shown in later figures.

Response: : As requested, we have added a new Figure 1 that shows the signature in Table 1 and the ‘expanded’ signature in COSMIC format to help illustrate Equation 1.

5. Note that reference 5 has an updated version: Omichessan, Severi & Perduca (2019)¹.

Response: Reference 5 is now updated.

6. Note that reference 6 is missing a colon between the author list and title.

Response: : The colon has been added to reference 6.

7. The "About iMutSig" web page states that "On the GitHub page, you can: - install the iMutSig R pacakge and run it locally." However, on the GitHub page I found no instructions on how the package can be installed and run locally using R and Shiny. While I understand that the main purpose of the platform is to be an online tool, some users may be interested in having a local copy. For example, the availability of the tool seemed somewhat variable: I was able to access the website (https://zhiyang.shinyapps.io/imutsig/) on 17 June, but not on 18 June. Although this might be a rare issue, it highlights the advantage of providing users with an alternative way of accessing the tool in the long term. For example, some simple steps for installation and running could be added as a README.md file on the GitHub repository.

Response: Thank you for the suggestion. A new README.md file was added to the GitHub repository (https://github.com/USCbiostats/iMutSig) providing instructions on how to install the necessary packages and host the app locally. The website failure on June 18^th resulted from a scheduled automatic downloading procedure which exceeded the server response time. Subsequently, we found that the COSMIC website posted new versions of signatures (v3.1) under a different website, allowing us to remove the automatic download procedure and avoid such an issue in the future.

8. Note that, in the platform interface, some of the signature names read "COSIMIC" instead of "COSMIC".

Response: Those typos have been corrected.

OPTIONAL SUGGESTIONS

9. I found it strange that in the tabs "COSMIC to pmsignature" and "pmsignature to COSMIC", the drop-down menus for choosing the COSMIC and PM signatures to compare are located in the middle of the interface, below the top panels that show the chosen signature. It seems to me that it would be more intuitive to place the selection menus at the top of the page, although I might be wrong.

Response: The dropdown menu for selection is now at the top of the webpage.

10. The authors might consider extending the user-supplied signature mode to allow the user to input a set of signatures, and then select the signature to compare using a drop-down menu (as in the other comparison modes), as it is likely that users will be interested in analysing sets of signatures, rather than single signatures. However, I understand this might not be straightforward to implement.

Response: Thank you for the suggestion. Indeed, allowing multiple signature inputs will require introducing a drop-down menu in order to maintain the current layout. Although not incorporated at this time, we plan to add this feature in the future.

11. Another potential extension could be an additional mode in which comparison could be performed between two sets of user-supplied signatures (each of which could be in COSMIC or PM format), in order to find the best one-to-one match between the signatures.

Response: Thank you for this suggestion as well. In the future, we also plan to add this feature by adding a tab allowing the comparison between user-supplied signatures.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 19 Nov 2020

Zhi Yang, Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, 91003, USA

19 Nov 2020

Author Response

We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: ... Continue reading We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: The formula for the cosine similarity defined in Equation 2 is not correct. While it is true that
CS(P,C) = (P·C) / (||P||·||C||),
it is not true that
CS(P,C) = sum(P_i * C_i) / (sum(P_i) * sum(C_i)).

The correct formula for the third part of Equation 2 would be:
CS(P,C) = sum(P_i * C_i) / (sqrt(sum(P_i^2)) * sqrt(sum(C_i^2)))
(see here).

Please amend this formula, and make sure that it gives the same values as the formula you have defined in your code (function getCosDistance).

Response: The formula has been corrected in this new version of the manuscript. We have also verified that the formula was correctly implemented in the getCosDistance function in the software (see below).

getCosDistance <- function(F_1, F_2) {

if(length(F_1)!=length(F_2)){
    geterrmessage("Two signatures have different number of bases!")
}

cos <- sum(F_1*F_2)/(sqrt(sum(F_1^2))*sqrt(sum(F_2^2)))
return(cos)
}

MINOR COMMENTS

2. Introduction, paragraph 1: This is somewhat inaccurate, in the sense that it is the cells in an organism's tissues that are exposed to mutational processes throughout the organism's life, and each cell or tissue develops its own mutational profile. The existence of a "unique mutational profile" thus may be better described as a property of a tissue, organ or tumour: it is not really accurate to say that each human has "his/her unique mutational profile", as this varies widely across tissues (e.g. cells in the blood, skin, liver, and colon have very different mutational spectra), and the differences among individuals also tend to be tissue-specific.

Response: We agree that our phrasing was poorly chosen here. We have altered the text to reflect this comment. The text now says “These processes result in a catalog of somatic mutations in the tissue creating…”.

3. Introduction, paragraph 3: in the sentence where the motivation for PM signatures is mentioned ("due to it requiring fewer parameters"), it might be appropriate to add a brief note that the assumption of independence between substitution type and flanking bases also limits the representation of patterns where these features are dependent, although this is seen in relatively few COSMIC signatures (e.g. SBS8, SBS25, SBS35).

Response: We have added a sentence addressing this disadvantage of using the independence assumption. “However, the independence assumption might prevent signatures with dependent bases from being discovered, thereby resulting in fewer signatures.”

4. Implementation, paragraph 1: it would be useful to complement the example in Table 1 and Equation 1 with a figure that shows the original PM signature in Table 1, and the equivalent COSMIC signature that results from applying Equation 1 to each of the 96 substitution types. This would help the reader to understand the conversion between both graphical representations, which is shown in later figures.

Response: : As requested, we have added a new Figure 1 that shows the signature in Table 1 and the ‘expanded’ signature in COSMIC format to help illustrate Equation 1.

5. Note that reference 5 has an updated version: Omichessan, Severi & Perduca (2019)¹.

Response: Reference 5 is now updated.

6. Note that reference 6 is missing a colon between the author list and title.

Response: : The colon has been added to reference 6.

7. The "About iMutSig" web page states that "On the GitHub page, you can: - install the iMutSig R pacakge and run it locally." However, on the GitHub page I found no instructions on how the package can be installed and run locally using R and Shiny. While I understand that the main purpose of the platform is to be an online tool, some users may be interested in having a local copy. For example, the availability of the tool seemed somewhat variable: I was able to access the website (https://zhiyang.shinyapps.io/imutsig/) on 17 June, but not on 18 June. Although this might be a rare issue, it highlights the advantage of providing users with an alternative way of accessing the tool in the long term. For example, some simple steps for installation and running could be added as a README.md file on the GitHub repository.

Response: Thank you for the suggestion. A new README.md file was added to the GitHub repository (https://github.com/USCbiostats/iMutSig) providing instructions on how to install the necessary packages and host the app locally. The website failure on June 18^th resulted from a scheduled automatic downloading procedure which exceeded the server response time. Subsequently, we found that the COSMIC website posted new versions of signatures (v3.1) under a different website, allowing us to remove the automatic download procedure and avoid such an issue in the future.

8. Note that, in the platform interface, some of the signature names read "COSIMIC" instead of "COSMIC".

Response: Those typos have been corrected.

OPTIONAL SUGGESTIONS

9. I found it strange that in the tabs "COSMIC to pmsignature" and "pmsignature to COSMIC", the drop-down menus for choosing the COSMIC and PM signatures to compare are located in the middle of the interface, below the top panels that show the chosen signature. It seems to me that it would be more intuitive to place the selection menus at the top of the page, although I might be wrong.

Response: The dropdown menu for selection is now at the top of the webpage.

10. The authors might consider extending the user-supplied signature mode to allow the user to input a set of signatures, and then select the signature to compare using a drop-down menu (as in the other comparison modes), as it is likely that users will be interested in analysing sets of signatures, rather than single signatures. However, I understand this might not be straightforward to implement.

Response: Thank you for the suggestion. Indeed, allowing multiple signature inputs will require introducing a drop-down menu in order to maintain the current layout. Although not incorporated at this time, we plan to add this feature in the future.

11. Another potential extension could be an additional mode in which comparison could be performed between two sets of user-supplied signatures (each of which could be in COSMIC or PM format), in order to find the best one-to-one match between the signatures.

Response: Thank you for this suggestion as well. In the future, we also plan to add this feature by adding a tab allowing the comparison between user-supplied signatures.
We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: The formula for the cosine similarity defined in Equation 2 is not correct. While it is true that
CS(P,C) = (P·C) / (||P||·||C||),
it is not true that
CS(P,C) = sum(P_i * C_i) / (sum(P_i) * sum(C_i)).

The correct formula for the third part of Equation 2 would be:
CS(P,C) = sum(P_i * C_i) / (sqrt(sum(P_i^2)) * sqrt(sum(C_i^2)))
(see here).

Please amend this formula, and make sure that it gives the same values as the formula you have defined in your code (function getCosDistance).

Response: The formula has been corrected in this new version of the manuscript. We have also verified that the formula was correctly implemented in the getCosDistance function in the software (see below).

getCosDistance <- function(F_1, F_2) {

if(length(F_1)!=length(F_2)){
    geterrmessage("Two signatures have different number of bases!")
}

cos <- sum(F_1*F_2)/(sqrt(sum(F_1^2))*sqrt(sum(F_2^2)))
return(cos)
}

MINOR COMMENTS

2. Introduction, paragraph 1: This is somewhat inaccurate, in the sense that it is the cells in an organism's tissues that are exposed to mutational processes throughout the organism's life, and each cell or tissue develops its own mutational profile. The existence of a "unique mutational profile" thus may be better described as a property of a tissue, organ or tumour: it is not really accurate to say that each human has "his/her unique mutational profile", as this varies widely across tissues (e.g. cells in the blood, skin, liver, and colon have very different mutational spectra), and the differences among individuals also tend to be tissue-specific.

Response: We agree that our phrasing was poorly chosen here. We have altered the text to reflect this comment. The text now says “These processes result in a catalog of somatic mutations in the tissue creating…”.

3. Introduction, paragraph 3: in the sentence where the motivation for PM signatures is mentioned ("due to it requiring fewer parameters"), it might be appropriate to add a brief note that the assumption of independence between substitution type and flanking bases also limits the representation of patterns where these features are dependent, although this is seen in relatively few COSMIC signatures (e.g. SBS8, SBS25, SBS35).

Response: We have added a sentence addressing this disadvantage of using the independence assumption. “However, the independence assumption might prevent signatures with dependent bases from being discovered, thereby resulting in fewer signatures.”

4. Implementation, paragraph 1: it would be useful to complement the example in Table 1 and Equation 1 with a figure that shows the original PM signature in Table 1, and the equivalent COSMIC signature that results from applying Equation 1 to each of the 96 substitution types. This would help the reader to understand the conversion between both graphical representations, which is shown in later figures.

Response: : As requested, we have added a new Figure 1 that shows the signature in Table 1 and the ‘expanded’ signature in COSMIC format to help illustrate Equation 1.

5. Note that reference 5 has an updated version: Omichessan, Severi & Perduca (2019)¹.

Response: Reference 5 is now updated.

6. Note that reference 6 is missing a colon between the author list and title.

Response: : The colon has been added to reference 6.

7. The "About iMutSig" web page states that "On the GitHub page, you can: - install the iMutSig R pacakge and run it locally." However, on the GitHub page I found no instructions on how the package can be installed and run locally using R and Shiny. While I understand that the main purpose of the platform is to be an online tool, some users may be interested in having a local copy. For example, the availability of the tool seemed somewhat variable: I was able to access the website (https://zhiyang.shinyapps.io/imutsig/) on 17 June, but not on 18 June. Although this might be a rare issue, it highlights the advantage of providing users with an alternative way of accessing the tool in the long term. For example, some simple steps for installation and running could be added as a README.md file on the GitHub repository.

Response: Thank you for the suggestion. A new README.md file was added to the GitHub repository (https://github.com/USCbiostats/iMutSig) providing instructions on how to install the necessary packages and host the app locally. The website failure on June 18^th resulted from a scheduled automatic downloading procedure which exceeded the server response time. Subsequently, we found that the COSMIC website posted new versions of signatures (v3.1) under a different website, allowing us to remove the automatic download procedure and avoid such an issue in the future.

8. Note that, in the platform interface, some of the signature names read "COSIMIC" instead of "COSMIC".

Response: Those typos have been corrected.

OPTIONAL SUGGESTIONS

9. I found it strange that in the tabs "COSMIC to pmsignature" and "pmsignature to COSMIC", the drop-down menus for choosing the COSMIC and PM signatures to compare are located in the middle of the interface, below the top panels that show the chosen signature. It seems to me that it would be more intuitive to place the selection menus at the top of the page, although I might be wrong.

Response: The dropdown menu for selection is now at the top of the webpage.

10. The authors might consider extending the user-supplied signature mode to allow the user to input a set of signatures, and then select the signature to compare using a drop-down menu (as in the other comparison modes), as it is likely that users will be interested in analysing sets of signatures, rather than single signatures. However, I understand this might not be straightforward to implement.

Response: Thank you for the suggestion. Indeed, allowing multiple signature inputs will require introducing a drop-down menu in order to maintain the current layout. Although not incorporated at this time, we plan to add this feature in the future.

11. Another potential extension could be an additional mode in which comparison could be performed between two sets of user-supplied signatures (each of which could be in COSMIC or PM format), in order to find the best one-to-one match between the signatures.

Response: Thank you for this suggestion as well. In the future, we also plan to add this feature by adding a tab allowing the comparison between user-supplied signatures.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 10 Jun 2020

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 19 Nov 20	read	read
Version 1 10 Jun 20	read	read

Adrian Baez-Ortega, University of Cambridge, Cambridge, UK
Vittorio Perduca, Université de Paris, CNRS, MAP5 UMR 8145, F-75006, Paris, France

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

10 Views

27 Nov 2020 | for Version 2

Adrian Baez-Ortega, Transmissible Cancer Group, Department of Veterinary Medicine, University of Cambridge, Cambridge, UK

10 Views Cite this report Responses(0)

Approved

In the iMutSig app, I noticed that the panel showing the membership of the selected COSMIC signature across tumour types does not display anything for some of the v3.1 signatures (e.g. SBS27, SBS28), while it does work for their v2 counterparts (e.g. C27, C28). I do not know if this is a mistake or if the distributions of some v3.1 signatures are really unknown.
Introduction, par. 2 reads: "thereby resulting a fewer signatures" instead of "thereby resulting in fewer signatures"; and "Shiraishi identified 27 signatures" instead of "Shiraishi et al. identified 27 signatures".
In Implementation, par. 1, when discussing the "expand" method whereby a COSMIC signature is constructed from three of the probabilities in the input PM signature, perhaps it would be good to mention that the PM signature may contain more features than just substitution type and immediate 5' and 3' bases (such as probabilities for -2/+2 bases and transcriptional strand), and that any information about these extra features of the PM signature is lost when "expanding" to the COSMIC format. Adding this comment might be valuable since the example in Table 1 does contain these extra features, and it would also highlight one of the strengths of PM signatures (more information in less parameters).
Implementation, par. 1 reads: "For example, to calculate the probability of the COSMIC signature C[C >A]T...". Should it not be "the COSMIC mutation type C[C>A]T"? A COSMIC signature would be a vector of 96 such mutation types/categories.
The comment above also applies to the next paragraph, which reads: "In a similar manner, the marginal probability of a flanking base is the sum of probabilities across all signatures containing the given flanking base."
Implementation, par. 2 reads: "To perform the “collapse” method, we calculate the marginal probability for each characteristic, the nucleotide substitution and each flanking base, and multiply the probabilities together using the independence assumption". Are you sure that the probabilities are multiplied together in the "collapse" method? As far as I understand, each marginal probability is obtained as a summation (as shown in Equation 2), and no multiplication is required afterwards – if I am correct, these marginal probabilities already define the PM signature.
Figure 2 legend reads: "The first two tabs allow users to finding...", instead of "to find".
Operation, par. 5 reads: "It is notable that the cosine similarity values tend to be higher using the collapse representation compared to the expand representation. We attribute this to the difference in model assumptions. When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not." While I understand this, I am not sure this is the only reason for the difference in cosine similarities. In general, one would expect high cosine similarity values to become less frequent as the number of dimensions increases; in other words, it is much less likely to find two 96-dimensional vectors with a near-zero angle between them than it is to find two 11-dimensional vectors with a similar angle. So it is possible that the mere fact of collapsing a COSMIC signature into a PM signature causes an overall increase in its cosine similarity with every other PM signature (and the opposite would be true when "expanding" signatures). However, I do not know which of these two explanations is more important for the change in similarity values observed in the signature heatmaps.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational biology, Bioinformatics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

9 Views

26 Nov 2020 | for Version 2

Vittorio Perduca, Université de Paris, CNRS, MAP5 UMR 8145, F-75006, Paris, France

9 Views Cite this report Responses(0)

Approved

Thank you for taking into account my comments and for clarifying the differences between the original "expand" method and the new "collapse" method. I have no further comments.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Applied statistics, biostatistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

40 Views

15 Jul 2020 | for Version 1

Vittorio Perduca, Université de Paris, CNRS, MAP5 UMR 8145, F-75006, Paris, France

40 Views Cite this report Responses(1)

Approved With Reservations

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.
My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?
In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.
I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

References

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Applied statistics, biostatistics.

Respond to this report

Responses (1)

Author Response

19 Nov 2020

Zhi Yang, Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, 91003, USA

One important point worth stressing is that the proposed solution for comparing "PM signatures" and "COSMIC signatures" is to represent the former lower dimensional probabilistic vectors in the larger space of the latter vectors. This is clearly explained in the methods, but I believe it is worth mentioning explicitly that this happens even when the input is of the COSMIC type.

Response: We now summarize explicitly the tasks the software performs at the end of the introduction: “iMutSig, an easy-to-use tool that allows users to 1) input a new mutational signature, 2) compare it using Cosine similarity to all published signatures from both the COSMIC and PM-signature databases, 3) identify the most similar signatures previously reported, and 4) to assemble the information characterizing those signatures using simple point-and-click navigation.”

My major concern is that the described method relies on the pmsignature assumption of independence between the mutation features. Could the authors comment about the possible limitations entailed by this assumption?

Response: We are not recommending one method over another, but are providing a means for comparing signatures that are estimated under the different modeling assumptions. One can transform the format of either signature type to the format used by the other signature type (PM signature to COSMIC or COSMIC to PM signature). In the original submission we only considered expanding the PM signature to the COSMIC format. In this revision we have added the capability of collapsing the COSMIC signature to the PM signature format (see response to next comment). These are not symmetric activities and can lead to differences in the identification of most similar signature from the opposite model. The new method of ‘collapsing’ the COSMIC signature is described in the section: “Methods/Implementation”. The consequences for identifying the most similar signature of the opposite type are described in the last paragraph under “Methods/Operation”.

In my understanding, another possibility would have been to represent "COSMIC signatures" as 11-dimensional "PM signatures" by eliminating through summation two features out of three. For instance, one could compute the "PM signature" component representing the probability of the substitution S=[C>A] as
P(S = [C>A]) = sum_{l, r} P(L=l, S=[C>A], R=r), where L and R denote the -1 and +1 flanking bases, and P(L=l, S=[C>A], R=r) is one of the 96 probabilities in the input "COSMIC signature". This approach does not rely on the pmsignature assumption of independence. (This solution does not make it possible to consider "PM signatures" with more than two flanking bases, but in any case the information about such extra bases is lost when converting "PM signatures" to "COSMIC signatures" using the method described in the paper). Have the authors explored this other method? A comment on this point could possibly help clarifying the reason why the authors have decided to rely on the independence assumption.

Response: Thank you for this suggestion. As we noted in our response to your last point, we have added this additional comparison to the app using a function implemented in the decompTumor2Sig package. Interestingly, the cosine similarity values tend to be higher using the above method. We interpret this in the paper as follows: “When a COSMIC signature is collapsed to the PM signature format the independence assumption is imposed on both signature types. However, when a PM signature is expanded to the COSMIC signature format, the PM signature probability vector still represents the fit under feature independence whereas the COSMIC signature does not. This difference in model assumptions results in lower estimates of cosine similarity.” (section Methods/Operation).

I suggest to add a figure with the heatmap showing the cosine similarity between the original 27 "PM signatures" and the 30 v2 "COSMIC signatures". This would help understanding the type of correspondence between the two databases.

Response: The heatmap is now added to the Shiny app and the manuscript.

Minor point:

"Implementation" paragraph, line 6: pm-signature -> pmsignature.

Response: We have corrected this typo in this version of the manuscript.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

44 Views

22 Jun 2020 | for Version 1

Adrian Baez-Ortega, Transmissible Cancer Group, Department of Veterinary Medicine, University of Cambridge, Cambridge, UK

44 Views Cite this report Responses(1)

Approved With Reservations

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Partly
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

References

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational biology, Bioinformatics.

Respond to this report

Responses (1)

Author Response

19 Nov 2020

Zhi Yang, Department of Preventive Medicine, Keck School of Medicine of the University of Southern California, 2001 N.Soto Street, Los Angeles, 91003, USA

We are very grateful to the reviewers for their comments and suggestions. We give detailed responses to each of those comments below.

MAJOR COMMENTS

1. Implementation, paragraph 2: The formula for the cosine similarity defined in Equation 2 is not correct. While it is true that
CS(P,C) = (P·C) / (||P||·||C||),
it is not true that
CS(P,C) = sum(P_i * C_i) / (sum(P_i) * sum(C_i)).

The correct formula for the third part of Equation 2 would be:
CS(P,C) = sum(P_i * C_i) / (sqrt(sum(P_i^2)) * sqrt(sum(C_i^2)))
(see here).

Please amend this formula, and make sure that it gives the same values as the formula you have defined in your code (function getCosDistance).

Response: The formula has been corrected in this new version of the manuscript. We have also verified that the formula was correctly implemented in the getCosDistance function in the software (see below).

getCosDistance <- function(F_1, F_2) {

if(length(F_1)!=length(F_2)){
geterrmessage("Two signatures have different number of bases!")
}

cos <- sum(F_1*F_2)/(sqrt(sum(F_1^2))*sqrt(sum(F_2^2)))
return(cos)
}

MINOR COMMENTS

2. Introduction, paragraph 1: This is somewhat inaccurate, in the sense that it is the cells in an organism's tissues that are exposed to mutational processes throughout the organism's life, and each cell or tissue develops its own mutational profile. The existence of a "unique mutational profile" thus may be better described as a property of a tissue, organ or tumour: it is not really accurate to say that each human has "his/her unique mutational profile", as this varies widely across tissues (e.g. cells in the blood, skin, liver, and colon have very different mutational spectra), and the differences among individuals also tend to be tissue-specific.

Response: We agree that our phrasing was poorly chosen here. We have altered the text to reflect this comment. The text now says “These processes result in a catalog of somatic mutations in the tissue creating…”.

3. Introduction, paragraph 3: in the sentence where the motivation for PM signatures is mentioned ("due to it requiring fewer parameters"), it might be appropriate to add a brief note that the assumption of independence between substitution type and flanking bases also limits the representation of patterns where these features are dependent, although this is seen in relatively few COSMIC signatures (e.g. SBS8, SBS25, SBS35).

Response: We have added a sentence addressing this disadvantage of using the independence assumption. “However, the independence assumption might prevent signatures with dependent bases from being discovered, thereby resulting in fewer signatures.”

4. Implementation, paragraph 1: it would be useful to complement the example in Table 1 and Equation 1 with a figure that shows the original PM signature in Table 1, and the equivalent COSMIC signature that results from applying Equation 1 to each of the 96 substitution types. This would help the reader to understand the conversion between both graphical representations, which is shown in later figures.

Response: : As requested, we have added a new Figure 1 that shows the signature in Table 1 and the ‘expanded’ signature in COSMIC format to help illustrate Equation 1.

5. Note that reference 5 has an updated version: Omichessan, Severi & Perduca (2019)¹.

Response: Reference 5 is now updated.

6. Note that reference 6 is missing a colon between the author list and title.

Response: : The colon has been added to reference 6.

7. The "About iMutSig" web page states that "On the GitHub page, you can: - install the iMutSig R pacakge and run it locally." However, on the GitHub page I found no instructions on how the package can be installed and run locally using R and Shiny. While I understand that the main purpose of the platform is to be an online tool, some users may be interested in having a local copy. For example, the availability of the tool seemed somewhat variable: I was able to access the website (https://zhiyang.shinyapps.io/imutsig/) on 17 June, but not on 18 June. Although this might be a rare issue, it highlights the advantage of providing users with an alternative way of accessing the tool in the long term. For example, some simple steps for installation and running could be added as a README.md file on the GitHub repository.

Response: Thank you for the suggestion. A new README.md file was added to the GitHub repository (https://github.com/USCbiostats/iMutSig) providing instructions on how to install the necessary packages and host the app locally. The website failure on June 18^th resulted from a scheduled automatic downloading procedure which exceeded the server response time. Subsequently, we found that the COSMIC website posted new versions of signatures (v3.1) under a different website, allowing us to remove the automatic download procedure and avoid such an issue in the future.

8. Note that, in the platform interface, some of the signature names read "COSIMIC" instead of "COSMIC".

Response: Those typos have been corrected.

OPTIONAL SUGGESTIONS

9. I found it strange that in the tabs "COSMIC to pmsignature" and "pmsignature to COSMIC", the drop-down menus for choosing the COSMIC and PM signatures to compare are located in the middle of the interface, below the top panels that show the chosen signature. It seems to me that it would be more intuitive to place the selection menus at the top of the page, although I might be wrong.

Response: The dropdown menu for selection is now at the top of the webpage.

10. The authors might consider extending the user-supplied signature mode to allow the user to input a set of signatures, and then select the signature to compare using a drop-down menu (as in the other comparison modes), as it is likely that users will be interested in analysing sets of signatures, rather than single signatures. However, I understand this might not be straightforward to implement.

Response: Thank you for the suggestion. Indeed, allowing multiple signature inputs will require introducing a drop-down menu in order to maintain the current layout. Although not incorporated at this time, we plan to add this feature in the future.

11. Another potential extension could be an additional mode in which comparison could be performed between two sets of user-supplied signatures (each of which could be in COSMIC or PM format), in order to find the best one-to-one match between the signatures.

Response: Thank you for this suggestion as well. In the future, we also plan to add this feature by adding a tab allowing the comparison between user-supplied signatures.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Alexandrov LB, Nik-Zainal S, Wedge DC, et al.: Signatures of mutational processes in human cancer. Nature. 2013; 500(7463): 415–21. PubMed Abstract | Publisher Full Text | Free Full Text

[2] 2. Yang Z, Pandey P, Shibata D, et al.: HiLDA: a statistical approach to investigate differences in mutational signatures. bioRxiv. 2019; 577452. Publisher Full Text

[3] 3. Gröschel S, Hübschmann D, Raimondi F, et al.: Defective homologous recombination DNA repair as therapeutic target in advanced chordoma. Nat Commun. 2019; 10(1): 1635. PubMed Abstract | Publisher Full Text | Free Full Text

[4] 4. Ülgen E, Can C, Bilguvar K, et al.: Whole exome sequencing–based analysis to identify DNA damage repair deficiency as a major contributor to gliomagenesis in adult diffuse gliomas. J Neurosurg. 2019; 1(aop): 1–12. PubMed Abstract | Publisher Full Text

[5] 5. Omichessan H, Severi G, Perduca V: Computational tools to detect signatures of mutational processes in DNA from tumours: a review and empirical comparison of performance. PLoS One. 2019; 14(9): e0221235. PubMed Abstract | Publisher Full Text | Free Full Text

[6] 6. Baez-Ortega A, Gori K: Computational approaches for discovery of mutational signatures in cancer. Brief Bioinform. 2017; 20(1): 77–88. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Forbes SA, Beare D, Boutselakis H, et al.: COSMIC: somatic cancer genetics at high-resolution. Nucleic Acids Res. 2016; 45(D1): D777–D783. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Alexandrov LB, Kim J, Haradhvala NJ, et al.: The repertoire of mutational signatures in human cancer. Nature. 2020; 578(7793): 94–101. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Shiraishi Y, Tremmel G, Miyano S, et al.: A simple model-based approach to inferring and visualizing cancer mutation signatures. PLoS Genet. 2015; 11(12): e1005657. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Nik-Zainal S, Loo PV, Wedge DC, et al.: The life history of 21 breast cancers. Cell. 2012; 149(5): 994–1007. PubMed Abstract | Publisher Full Text | Free Full Text

[11] 11. Schulze K, Imbeaud S, Letouzé E, et al.: Exome sequencing of hepatocellular carcinomas identifies new mutational signatures and potential therapeutic targets. Nat Genet. 2015; 47(5): 505–511. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Helleday T, Eshtad S, Nik-Zainal S: Mechanisms underlying mutational signatures in human cancers. Nat Rev Genet. 2014; 15(9): 585–98. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Yokoyama A, Kakiuchi N, Yoshizato T, et al.: Age-related remodelling of oesophageal epithelia by mutated cancer drivers. Nature. 2019; 565(7739): 312–317. PubMed Abstract | Publisher Full Text

[14] 14. Guo J, Huang J, Zhou Y, et al.: Germline and somatic variations influence the somatic mutational signatures of esophageal squamous cell carcinomas in a chinese population. BMC Genomics. 2018; 19(1): 538. PubMed Abstract | Publisher Full Text | Free Full Text

[15] 15. Krüger S, Piro RM: decompTumor2Sig: Identification of mutational signatures active in individual tumors. BMC Bioinformatics. 2019; 20(Suppl 4): 152. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Yang Z: USCbiostats/iMutSig v1.2 (version v1.2). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.4132416

iMutSig: a web application to identify the most similar mutational signature using shiny

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Methods

Implementation

Table 1. An example of PM signatures.

Figure 1. The PM signature appearing in Table 1 (top) with the ‘expanded’ signature appearing in COSMIC format (bottom).

Operation

Figure 2. Overview of three workflows in the iMutSig interface.

Figure 3. Cosine similarity heatmaps between PM signatures and COSMIC signatures.

Use cases

Figure 4. Input a COSMIC v3.1 signature, SBS1.

Figure 5. Input a PM signature, P1.

Figure 6. Input a user-supplied COSMIC signature.

Figure 7. Input a user-supplied PM signature.

Conclusions

Data availability

Software availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated