Keywords
transcription-factors, DNA-binding, gene-expression, r-package, bioconductor, workflow
This article is included in the RPackage gateway.
This article is included in the Cell & Molecular Biology gateway.
This article is included in the Bioinformatics gateway.
This article is included in the Bioconductor gateway.
transcription-factors, DNA-binding, gene-expression, r-package, bioconductor, workflow
The following changes were made in this revised version of the article:
See the authors' detailed response to the review by Mireia Ramos-Rodríguez
See the authors' detailed response to the review by Shulan Tian and Yan Huihuang
The binding of a transcription factor to a genomic region (e.g., gene promoter) can have the effect of inducing or repressing its expression Latchman1. The binding sites can be identified using ChIP experiments. High through-put ChIP experiments produce hundreds or thousands of binding sites for most factors Johnson et al.2. Therefore, methods to determine which of these sites are true binding sites and whether they are functional or not are needed Ucar et al.3. On the other hand, perturbing the transcription factor by over-expression or knockdown and measuring the gene expression changes provide valuable information on the function of the factor Tran et al.4. Methods exist to integrate the binding data and the factor perturbation gene expression to predict the real target regions (e.g., genes)5,6. This article presents a workflow for using the target package to integrate binding and expression data to predict the shared targets and the combined function of two transcription factors.
To illustrate the utility of this workflow, we applied it to the binding and expression data of the transcription factors YY1 and YY2. We asked whether the two factors cooperate or compete on their shared targets in HeLa cells.
We developed an open-source R/Bioconductor package target to implement BETA for predicting direct transcription factor targets from binding and expression data. The details of the algorithm were described here Wang et al.6. In addition, our implementation extends BETA to apply for factor combinations (Ahmed et al.7). Briefly, we identify the factor potential binding sites by ChIP-sequencing and gene expression under factor perturbation by microarrays or sequencing. Next, we score the peaks based on their distances to the transcription start sites. The sum of the scores of the individual peaks in a certain region of interest is the region’s regulatory potential. The signed statistics (fold-change or t-statistics) from the differential gene expression of the factor perturbation reflect the factor effects. The product of the ranks of the regulatory potential and the signed statistics is the final rank of the regions.
To predict the combined function of two factors, two sets of data are required. The overlapping peaks are the potential binding sites. The product of the two signed statistics is the factor function. When the two factors agree in the direction of the regulation of a region where they both bind, they could be said to cooperate on this region. When the sign is opposite, they could be said to regulate that region competitively.
The package leverages the Bioconductor data structures such as GRanges and DataFrame to provide fast and flexible computation on the data Huber et al.8. Similar to the original python implementation, the input data are the identified peaks from the ChIP-Seq experiment and the expression data from RNA-Seq or microarrays perturbation experiment. The final output is the peaks associated with the factor binding and the predicted direct targets. We use the terms “peaks” to refer to the GRanges object that contains the coordinates of the peaks. Likewise, we use the term “region” to refer to a similar object that contains the information on the regions of interest; genes, transcripts, promoter regions, etc. In both cases, additional information on the ranges can be added to the object as metadata.
The algorithm was implemented in R (>= 3.6) and should run on any operating system. Libraries required for running the workflow are listed and loaded below. Alternatively, a docker image is available with R and the libraries installed on an Ubuntu image: https://hub.docker.com/r/bcmslab/target_flow.
# load required libraries library(GenomicRanges) library(Biostrings) library(rtracklayer) library(TxDb.Hsapiens.UCSC.hg19.knownGene) library(BSgenome.Hsapiens.UCSC.hg19) library(org.Hs.eg.db) library(tidyverse) library(BCRANK) library(seqLogo) library(target)
YY1 and YY2 belong to the same family of transcription factors. YY1 is a zinc finger protein that directs histone deacetylase and acetyltransferases of the promoters of many genes. The protein also binds to the enhancer regions of many of its targets. The binding of YY1 to the regulatory regions of genes results in the induction or repression of their expression. YY2 is a paralog of YY1. Similarly, it is a zinc finger protein with both activation or repression functions on its targets. We will attempt to answer the following questions using the target analysis: Do the two transcription factors share the same target genes? What are the consequences of the binding of each factor on its targets? If the two factors share binding sites, what is the function of the two factors binding to these sites?
To answer these questions, we use publicly available datasets to model the binding and gene expression under the transcription factors perturbations (Table 1). This dataset was obtained in the form of differential expression between the two conditions from KnockTF Feng et al.9. The first dataset is gene expression profiling using microarrays of YY1/YY2 knockdown and control HeLa cells. Next, the binding sites of the factors in HeLa cells were determined using two ChIP-Seq datasets. The ChIP peaks were acquired in the form of bed files from ChIP-Atlas Oki et al.10. Finally, we used the UCSC hg19 human genome to extract the genomic annotations.
| GEO ID | Data Type | Design | Ref. |
|---|---|---|---|
| GSE14964 | Microarrays | YY#-knockdown | Chen et al.11 |
| GSE31417 | ChIP-Seq | YY1 vs input | Michaud et al.12 |
| GSE96878 | ChIP-Seq | YY2 vs input | Wu et al.13 |
Briefly, we first prepared the three sources of data for the target analysis. Then we predict the specific targets for each individual factor. Third, we predict the combined function of the two factors on the shared target genes. Finally, we show an example of a motif analysis of the competitively and cooperatively regulated targets.
if(!file.exists('data.zip')) { # download the manuscript data download.file('https://ndownloader.figshare.com/articles/10918463/versions/1', destfile = 'data.zip') # decompress file unzip('data.zip', exdir = 'data') }
The ChIP peaks were downloaded in the form of separate bed files for each factor. We first locate the files in the data/ directory and load the files using import.bed. Then the data is transformed into a suitable format, GRanges. The resulting object, peaks, is a list of two GRanges items, one for each factor.
# locate the peaks bed files peak_files <- c(YY1 = 'data/Oth.Utr.05.YY1.AllCell.bed', YY2 = 'data/Oth.Utr.05.YY2.AllCell.bed') # load the peaks bed files as GRanges peaks <- map(peak_files, ~GRanges(import.bed(.x)))
The differential expression data were downloaded in tabular format. After locating the files in data/, we read the files using read_tsv and select and rename the relevant columns. The resulting object, express, is a list of two tibble items.
# locate the expression text files expression_files <- c(YY1 = 'data/DataSet_01_18.tsv', YY2 = 'data/DataSet_01_19.tsv') # load the expression text files express <- map(expression_files, ~read_tsv(.x, col_names = FALSE) %>% dplyr::select(2, 3, 7, 9) %>% #9 setNames(c('tf', 'gene', 'fc', 'pvalue')) %>% filter(tf %in% c('YY1', 'YY2')) %>% na.omit())
The knockdown of either factor in HeLa cells seems to change the expression of many genes in either direction (Figure 1A&B). Moreover, the changes resulting from the separate knockdown of the factors are correlated (Figure 1C). These observations suggest that many of the regulated genes are shared targets of the two factors, or they respond similarly to their perturbation of either factor.
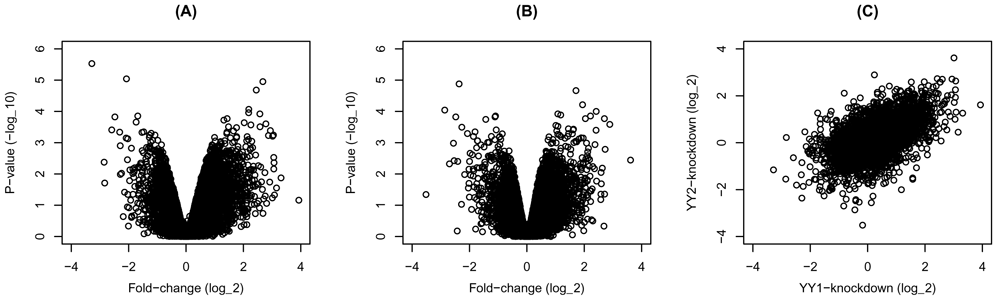
Gene expression was compared between transcription factors knockdown and control HeLa cells. The fold-change and p-values of (A) YY1- and (B) YY2-knockdown are shown as volcano plots. (C) Scatter plot of the fold-change of the YY1- and YY2-knockdown.
# Figure 1 par(mfrow = c(1, 3)) # volcano plot of YY1 knockdown plot(express$YY1$fc, -log10(express$YY1$pvalue), xlab = 'Fold-change (log_2)', ylab = 'P-value (-log_10)', xlim = c(-4, 4), ylim = c(0, 6)) title('(A)') # volcano plot of YY2 knockdown plot(express$YY2$fc, -log10(express$YY2$pvalue), xlab = 'Fold-change (log_2)', ylab = 'P-value (-log_10)', xlim = c(-4, 4), ylim = c(0, 6)) title('(B)') # plot fold-change of YY1 and YY2 plot(express$YY1$fc[order(express$YY1$gene)], express$YY2$fc[order(express$YY2$gene)], xlab = 'YY1-knockdown (log_2)', ylab = 'YY2-knockdown (log_2)', xlim = c(-4, 4), ylim = c(-4, 4)) title('(C)')
express records the gene information using the gene Symbols. We mapped the Symbols to the Entrez IDs before extracting the genomic coordinates. To do that, we use the org.Hs.eg.db to convert between the identifiers. Next, we use the TxDb.Hsapiens.UCSC.hg19.knownGene to get the genomic coordinates for the transcripts and extend them to 100kb upstream from the transcription start sites.
# load genome data symbol_entrez <- AnnotationDbi::select(org.Hs.eg.db, unique(c(express$YY1$gene)), 'ENTREZID', 'SYMBOL') %>% setNames(c('gene', 'gene_id')) # format genome to join with express genome <- promoters(TxDb.Hsapiens.UCSC.hg19.knownGene, upstream = 100000, columns = c('tx_id', 'tx_name', 'gene_id')) %>% as_tibble() %>% mutate(gene_id = as.character(gene_id))
The resulting object, genome, from the previous step is a tibble that shares the column gene_id with the expression data express. Now the two objects can be merged. The merged object, regions, is similarly a tibble containing genome and expression information of all common genes.
# make regions by merging the genome and express data regions <- map(express, ~inner_join(genome, symbol_entrez) %>% inner_join(.x) %>% makeGRangesFromDataFrame(keep.extra.columns = TRUE))
The standard target analysis identifies associated peaks using associated_peaks and direct targets using direct_targets. The inputs for these functions are the objects peaks and regions from the previous steps in addition to the column names for regions regions_col or the region and the statistics column stats_col, which is the fold-change in this case. The resulting objects are GRanges for the identified peaks assigned to the regions, ap, or the ranked targets. Several columns are added to the metadata objects of the GRanges to save the output.
# get associated peaks ap <- map2(peaks, regions, ~associated_peaks(peaks=.x, regions = .y, regions_col = 'tx_id')) # get direct targets dt <- map2(peaks, regions, ~direct_targets(peaks=.x, regions = .y, regions_col = 'tx_id', stats_col = 'fc'))
To determine the dominant function of a factor, we divide the targets by the direction of the effect of factor knockdown. We group the targets by the change in gene expression (regulatory potential). We use the empirical distribution function (ECDF) to show the fraction of targets with a specified regulatory potential or less. Because we use the ranks rather than the absolute value of the regulatory potential, the lower the rank, the higher the potential. Then, {we compare} the groups of targets to each other or to a theoretical distribution.
# Figure 2 par(mfrow = c(1, 3)) # plot distance by score of associate peaks plot(ap$YY1$distance, ap$YY1$peak_score, xlab = 'Distance', ylab = 'Peak Score', main = '(A)') points(ap$YY2$distance, ap$YY2$peak_score) # make labels, colors and groups labs <- c('Down', 'None', 'Up') cols <- c('green', 'gray', 'red') # make three groups by quantiles groups <- map(dt,~{ cut(.x$stat, breaks = 3, labels = labs) }) # plot the group functions pmap(list(dt, groups, c('(B)', '(C)')), function(x, y, z) { plot_predictions(x$score_rank, group = y, colors = cols, labels = labs, xlab = 'Regulatory Potential', ylab = 'ECDF') title(z) })
The scores of the individual peaks are a decreasing function of the distance from the transcription start sites— the closer the factor binding site from the start site, the higher the score. The distribution of these scores is very similar for both factors (Figure 2A). The ECDF of the down-regulated of YY1 is higher than that of up-and none-regulated targets (Figure 2B). Therefore, the absence of YY1 on its targets results in aggregate in their downregulation. If indeed these are true targets, then we expect YY1 to induce their expression. The opposite is true for YY2, where more high-ranking targets are up-regulated by the factor knockdown (Figure 2C).
# Table 2 # test individual factor functions map2(dt, groups, ~test_predictions(.x$rank, group = .y, compare = c('Down', 'Up')))
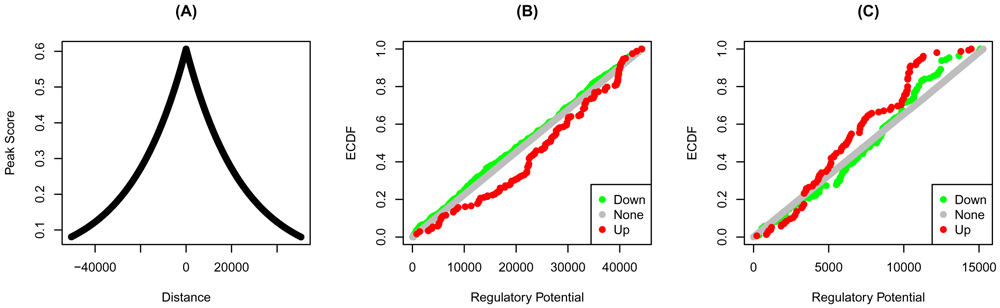
Bindings peaks of the transcription factors in HeLa cells were determined using ChIP-Seq. Distances from the transcription start sites, and the transformed distances of the (A) YY1 and YY2 peaks are shown. The regulatory potential of each gene was calculated using target. Genes were grouped into up, none, or down-regulated based on the fold-change. The empirical cumulative distribution functions (ECDF) of the groups of (C) YY1 and (C) YY2 targets are shown at each regulatory potential rank.
To formally test these observations, we use the Kolmogorov-Smirnov (KS) test. First, we compare the distributions of the two groups for equality. If one lies on either side of the other, then they must be drawn from different distributions. Here, we contrast the up and down-regulated functions for both factors (Table 2). In both cases, the distributions of the two groups were significantly different from one another.
Using target to predict the shared target genes and the combined function of the two factors is a variation of the previous analysis. First, the shared/common peaks are generated using the overlap of their genomic coordinates, subsetByOverlaps. Second, Instead of one, two columns for the differential expression statistics, one for each factor is needed; these are supplied to the argument stats_col in the same way. Here, common_peaks and both_regions are the main inputs for the analysis functions.
# merge and name peaks common_peaks <- GenomicRanges::reduce(subsetByOverlaps(peaks$YY1, peaks$YY2)) common_peaks$name <- paste0('common_peak_', 1:length(common_peaks))
# bind express tables into one both_express <- bind_rows(express) %>% nest(fc, pvalue, .key = 'values_col') %>% spread(tf, values_col) %>% unnest(YY1, YY2, .sep = '_')
# make regions using genome and expression data of both factors both_regions <- inner_join(genome, symbol_entrez) %>% inner_join(both_express) %>% makeGRangesFromDataFrame(keep.extra.columns = TRUE)
# get associated peaks with both factors common_ap <- associated_peaks(peaks = common_peaks, regions = both_regions, regions_col = 'tx_id') # get direct targets of both factors common_dt <- direct_targets(peaks = common_peaks, regions = both_regions, regions_col = 'tx_id', stats_col = c('YY1_fc', 'YY2_fc'))
The output, associated_peaks, is similar to before. direct_targets is the same, but the stat and the stat_rank columns carry the product and the rank of the two statistics provided in the previous step.
We can also visualize the output in a similar way. The targets are divided into three groups based on the statistics product. When the two statistics agree in the sign, the product is positive. This means the knockdown of either transcription factor results in the same direction change in the target gene expression. Therefore, the two factors would cooperate if they bind to the same site on that gene. The reverse is true for targets with oppositely signed statistics. The two factors would be expected to compete on these targets for inducing opposing changes in the expression.
# Figure 3 par(mfrow = c(1, 2)) # plot distiace by score for associated peaks plot(common_ap$distance, common_ap$peak_score, xlab = 'Distance', ylab = 'Peak Score') title('(A)') # make labels, colors and gorups labs <- c('Competitive', 'None', 'Cooperative') cols <- c('green', 'gray', 'red') # make three groups by quantiles common_groups <- cut(common_dt$stat, breaks = 3, labels = labs) # plot predicted function plot_predictions(common_dt$score_rank, group = common_groups, colors = cols, labels = labs, xlab = 'Regulatory Interaction', ylab = 'ECDF') title('(B)')
The common peak distances and scores take the same shape (Figure 3A). Furthermore, the two factors seem to cooperate on more of the common target than any of the two other possibilities (Figure 3B). This observation can be tested using the KS test. The curve of the cooperative targets lies above that of none and competitively regulated targets (Table 3).

Shared bindings sites of YY1 and YY2 in HeLa cells were determined using the overlap of the individual factor ChIP-Seq peaks. (A) Distances from the transcription start sites, and the transformed distances of the shared peaks are shown. The regulatory interaction of each gene was calculated using target. Genes were grouped into cooperatively, none, or competitively regulated based on the product of the fold-changes from YY1- and YY2-knockdown. (B) The empirical cumulative distribution functions (ECDF) of the targets groups are shown at each regulatory potential rank.
# Table 3 # test factors are cooperative test_predictions(common_dt$score_rank, group = common_groups, compare = c('Cooperative', 'None'), alternative = 'greater') # test factors are more cooperative than competitive test_predictions(common_dt$score_rank, group = common_groups, compare = c('Cooperative', 'Competitive'), alternative = 'greater')
The users can perform any number of downstream analyses on the final output. For example, we could apply binding motif analysis to the groups of regulated targets. In this example, all the motif analysis itself is handled by the BCRANK package Ameur et al.14. Here, we explain how to prepare the input from the shared peaks and target objects produced in the last step.
First, we extract the transcript IDs of the targets in their respective groups. Then the peaks assigned to these targets are ordered and sliced.
# group peaks by their assigned targets peak_groups <- split(common_dt$tx_id, common_groups) # reorder peaks and get top n peaks peak_groups <- lapply(peak_groups, function(x) { # get peaks in x targets group p <- common_ap[common_ap$assigned_region %in% unique(x)] # order peaks by score p <- p[order(p$peak_score, decreasing = TRUE)] # get n top peaks p[seq_len(ifelse(length(p) > 50, 50, length(p)))] })
The input for bcrank is a fasta file with the sequence of the regions to look for frequent motifs. We used the BSgenome.Hsapiens.UCSC.hg19 to extract the sequences of the common peaks in the competitive and cooperative target groups. The sequences are first written to a temporary file and feed to the search function.
bcout <- map(peak_groups[c('Competitive', 'Cooperative')], ~{ # extract sequences of top peaks from the hg19 genome pseq <- getSeq(BSgenome.Hsapiens.UCSC.hg19, names = .x) # write sequences to fasta file tmp_fasta <- tempfile() writeXStringSet(pseq, tmp_fasta) # set random see set.seed(1234) # call bcrank with the fasta file bcrank(tmp_fasta, silent = TRUE) })
The sequences in the search path of the regions of interest are shown in (Figure 4). In the competitively regulated regions, one sequence was more frequent than all other sequences. By contrast, no sequence was uniquely frequent in the regions of cooperative targets.
# Figure 4 par(mfrow = c(1, 2)) # plot the occurrences of consensus sequesnce in the regions map2(bcout, c('(A)', '(B)'), ~{ plot(toptable(.x, 1)) title(.y) })
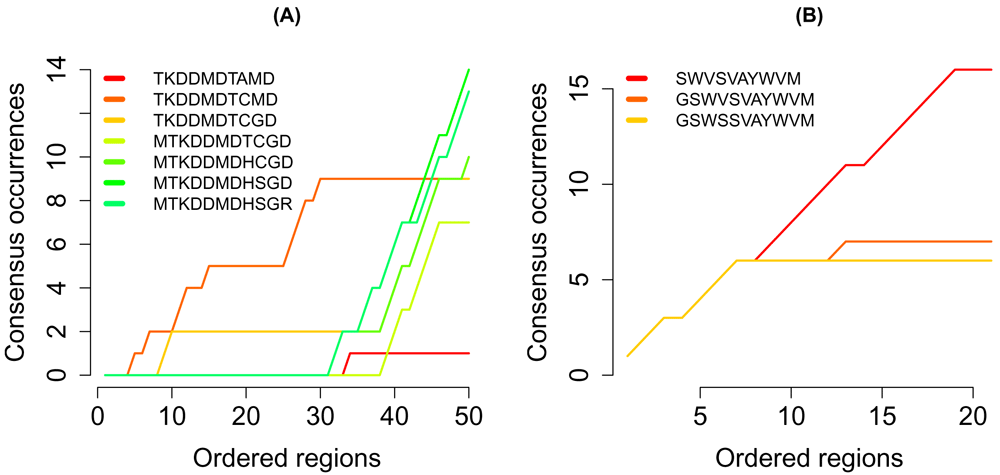
The number of occurances of the sequences in the search path in the regions of (A) competitively and (B) cooperatively regulated regions.
The most frequent motifs in the two groups are shown as seq logos using the seqLogo package (Figure 5).
# Figure 5 # plot the sequence of the predicted motifs map(bcout, c('(A)', '(B)'), ~{ seqLogo(pwm(toptable(.x, 1))) title(.y) })
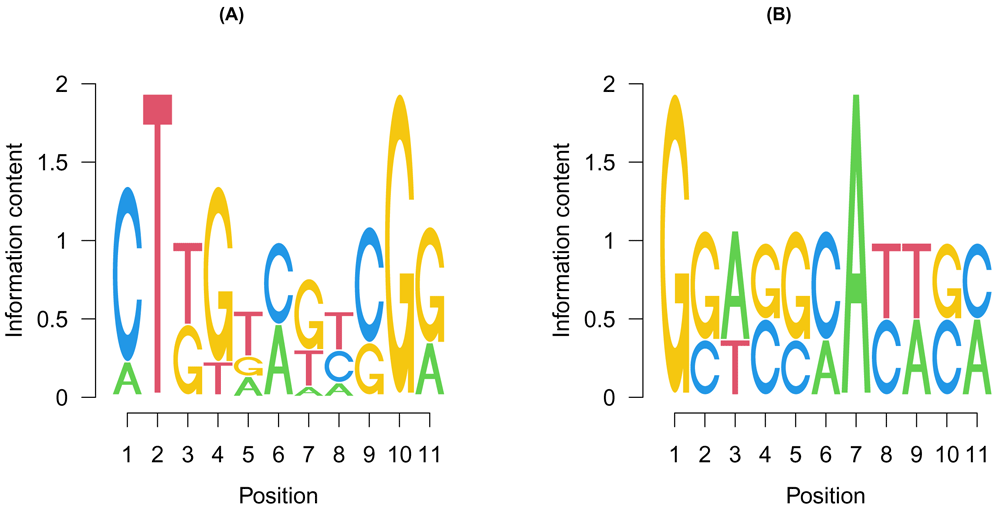
The position weight matrices of the most frequent motifs in the (A) competitively and (B) cooperatively regulated regions were calculated and shown as sequence logos. y-axis represents the information content at each position. The size of each letter represents the frequency in which the letter occurs at that position.
In this article, we present a workflow for predicting the direct targets of a transcription factor by integrating binding and expression data. The target package implements the BETA algorithm ranking gene targets based on the distances of the ChIP peaks of the transcription factor relative to the TSSs of the genes and the differential expression of the factor perturbation. To predict the combined function of two factors, two sets of data are used to find the shared peaks and the rank product of their differential expression statistics.
All data underlying the results are available as part of the article and no additional source data are required.
Software available from: https://doi.org/doi:10.18129/B9.bioc.target15
Source code available from: https://github.com/MahShaaban/target
Archived source code as at time of publication: https://doi.org/doi:10.18129/B9.bioc.target15
License: GPL-3
MA. Convinced the idea and wrote the draft of the manuscript. DK. Contributed to writing and revising the manuscript.
We thank all lab members for the discussion and comments on the early drafts of the article.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Yes
References
1. Wilkinson FH, Park K, Atchison ML: Polycomb recruitment to DNA in vivo by the YY1 REPO domain.Proc Natl Acad Sci U S A. 2006; 103 (51): 19296-301 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Genomics and Regulatory Genomics, Bioinformatics, R and Bioconductor.
Is the rationale for developing the new software tool clearly explained?
Yes
Is the description of the software tool technically sound?
Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?
Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?
Partly
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?
Yes
References
1. Weintraub AS, Li CH, Zamudio AV, Sigova AA, et al.: YY1 Is a Structural Regulator of Enhancer-Promoter Loops.Cell. 2017; 171 (7): 1573-1588.e28 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Genomics, bioinformatics, epigenomics, data science, etc
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||
|---|---|---|
| 1 | 2 | |
|
Version 4 (revision) 03 Aug 22 |
||
|
Version 3 (revision) 16 Nov 21 |
read | read |
|
Version 2 (revision) 10 Nov 21 |
||
|
Version 1 05 May 21 |
read | read |
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)