Improving genomic prediction of rhizomania resistance in sugar beet (<i>Beta vulgaris</i> L.) by implementing epistatic effects and feature selection

Thomas Martin Lange; Felix Heinrich; Friedrich Kopisch-Obuch; Harald Keunecke; Mehmet Gültas; Armin O. Schmitt

doi:10.12688/f1000research.131134.1

Home Browse Improving genomic prediction of rhizomania resistance in sugar beet...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Research Article

Improving genomic prediction of rhizomania resistance in sugar beet (Beta vulgaris L.) by implementing epistatic effects and feature selection

[version 1; peer review: 3 not approved]

Thomas Martin Lange¹, Felix Heinrich¹, Friedrich Kopisch-Obuch², Harald Keunecke², Mehmet Gültas³, Armin O. Schmitt^1,4

Thomas Martin Lange¹, Felix Heinrich¹, [...] Friedrich Kopisch-Obuch², Harald Keunecke², Mehmet Gültas³, Armin O. Schmitt^1,4

PUBLISHED 14 Mar 2023

Author details Author details

¹ Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany
² KWS Saat SE & Co. KGaA, Einbeck, 37574, Germany
³ Faculty of Agriculture, South Westphalia University of Applied Sciences, Soest, 59494, Germany
⁴ Center of Integrated Breeding Research (CiBreed), Göttingen, 37075, Germany

Thomas Martin Lange
Roles: Formal Analysis, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Felix Heinrich
Roles: Formal Analysis, Methodology, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Friedrich Kopisch-Obuch
Roles: Investigation, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Harald Keunecke
Roles: Investigation, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Mehmet Gültas
Roles: Conceptualization, Investigation, Methodology, Project Administration, Supervision, Validation, Writing – Review & Editing

Armin O. Schmitt
Roles: Conceptualization, Investigation, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Bioinformatics gateway.

This article is included in the Genomics and Genetics gateway.

This article is included in the Plant Computational and Quantitative Genomics collection.

Abstract

Background: Rhizomania counts as the most important disease in sugar beet Beta vulgaris L. for which no plant protection is available, leaving plant breeding as the only defence strategy at the moment. Five resistance genes have been detected on the same chromosome and further studies suggested that these might be different alleles at two resistance clusters. Nevertheless, it was postulated that rhizomania resistance might be a quantitative trait with multiple unknown minor resistance genes. Here, we present a first attempt at genomic prediction of rhizomania resistance in a population that was genotyped using single nucleotide polymorphism (SNP) markers.
Methods: First, genomic prediction was performed using all SNPs. Next, we calculated the variable importance for each SNP using machine learning and performed genomic prediction by including the SNPs incrementally in the prediction model based on their variable importance. Using this method, we selected the optimal number of SNPs that maximised the prediction accuracy. Furthermore, we performed genomic prediction with SNP pairs. We also performed feature selection with SNP pairs using the information about the variable importance of the single SNPs.
Results: From the four methods under investigation, the latter led to the highest prediction accuracy. These results lead to the following conclusions: (I) The genotypes that were resistant at all known resistance genes, provided the highest possible variation of virus concentrations that the machine can measure. Thus, it can be assumed that more genes must be involved in the resistance towards rhizomania. (II) We show that prediction models that include SNP interactions increased the prediction accuracy.
Conclusions: Altogether, our findings suggest that rhizomania resistance is a complex quantitative trait that is affected by multiple genes as well as their interaction.

Keywords

Epistasis, genomic prediction, machine learning, rhizomania, resistance breeding, Beet necrotic yellow vein virus, variable importance

Corresponding authors: Mehmet Gültas, Armin O. Schmitt

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2023 Lange TM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Lange TM, Heinrich F, Kopisch-Obuch F et al. Improving genomic prediction of rhizomania resistance in sugar beet (Beta vulgaris L.) by implementing epistatic effects and feature selection [version 1; peer review: 3 not approved]. F1000Research 2023, 12:280 (https://doi.org/10.12688/f1000research.131134.1) First published: 14 Mar 2023, 12:280 (https://doi.org/10.12688/f1000research.131134.1) Latest published: 28 Aug 2024, 12:280 (https://doi.org/10.12688/f1000research.131134.2)

Introduction

Sugar beet (Beta vulgaris L.) is an important crop to secure production of white sugar, especially in industrialised countries.¹ In general, sugar beet makes up 20% of the sugar production in the world.² Next to high sugar yield, resistance to diseases, of which rhizomania is the most significant, is the main goal of sugar beet breeding.³

Rhizomania is caused by the Beet necrotic yellow vein virus (BNYVV)⁴ and is transmitted via the fungus Polymyxa betae Keskin.⁵^,⁶ Severe infection with rhizomania can cause a reduced sugar yield of up to 90%.⁷ Moreover, Abe and Tamada (1986) have shown that rhizomania can persist in resting spores of P. betae for over fifteen years, making a decontamination through an enlarged crop rotation nearly impossible.⁸ Furthermore, there is no pesticide available for plant protection,⁹ leaving resistance breeding as the only defence strategy at the moment.¹⁰

Since the first observation of rhizomania in 1951 in northern Italy, the disease has spread globally and occurs nowadays in all major sugar beet growing regions in the world.¹¹ While strain groups of BNYVV with four ribonucleic acid (RNA) strands are spread globally,¹² BNYVV strains with five RNA strands have been found in certain regions in France,¹³ Japan,¹⁴ the UK,¹⁵ Kazakhstan,¹⁶ and Turkey.⁷ Comparisons between their pathogenicities revealed that pathotypes of BNYVV with five RNA strands showed significantly higher levels of infection in partially resistant sugar beet varieties than pathotypes with four RNA strands.¹⁷

The first breeding projects against rhizomania started in 1970¹⁸ and resulted in the publication of three resistance genes in 1987 called “Rizor”,¹⁹ “Holly”,²⁰ and “WB42”.²⁰ Nevertheless, further analyses of the resistance genes “Rizor” and “Holly” indicated that these are probably the same gene, henceforth called “Rz1”.²¹ The resistance gene “WB42” which is also often referred to as “Rz2”, however, was assumed to be a further resistance gene independent from Rz1 with an approximate distance of 20 cM between Rz1 and Rz2.²² Recent studies could not only prove the existence of the Rz2 resistance gene in wild relatives of sugar beet but also found a stop codon in Rz2 in susceptible genotypes which was not present in resistant genotypes.²³ In the following years, three further resistance genes were published called “Rz3”,²⁴ “Rz4”,²⁵ and “Rz5”.²⁶

Although five resistance genes against rhizomania have been published, doubts have been raised on whether all resistance genes are in fact separate genes or rather alleles of the same genes. All five resistance genes were located on chromosome three¹⁸^,²⁵^,²⁶ where mainly two clusters emerged.²⁷ McGrann et al. (2009) assumed that the resistance against rhizomania may be mainly explained by two loci, with the first locus being represented by Rz1, Rz4, and Rz5, and the second locus being represented by Rz2 and Rz3.¹² Although only two resistance clusters against rhizomania are known, it is assumed that rhizomania resistance is a quantitative trait caused by multiple loci with different effects, which have not yet been identified.¹⁸

In general, it has also been postulated that asymmetric variation in quantitative traits can be caused by epistasis.²⁸ Epistasis can be defined as non-additive interaction between genes.²⁹ Theoretically, this interaction can be formed by more than two genes but the analysis of an interaction between more than two genes is challenging due to the computational complexity and the requirement to have large enough samples for each subgroup.³⁰ Although it has been demanded to analyse epistasis in complex trait studies³¹^,³² and epistasis has been analysed for a multitude of traits in sugar beet,³³ such a study has not yet been conducted for rhizomania resistance to the best of our knowledge.

It is generally assumed that a plant’s resistance towards diseases is quantitative and caused by a complex network of multiple loci.³⁴^,³⁵ In such cases, genomic prediction is a useful tool to predict an individual’s resistance towards the disease. Such studies have been performed, for example, in soy bean,³⁶ barley,³⁷ rapeseed,³⁸ rice,³⁹ wheat,⁴⁰ and maize.⁴¹^,⁴² Although rhizomania resistance is believed to be a complex trait caused by multiple loci, genomic prediction of rhizomania resistance has not yet been published. Here, we present the first study of genomic prediction of rhizomania resistance with 9,127 single nucleotide polymorphism (SNP) markers in a sugar beet population that is assumed to carry the known resistance genes (Rz1 and Rz2).

Our aim is to maximise the accuracy of genomic prediction of rhizomania resistance in sugar beet. Therefore, we performed genomic prediction using random forest with all available SNP markers. Moreover, we estimated the variable importance of each SNP and, subsequently, performed incremental feature selection to optimise the prediction model by only including an optimal set of SNPs. Furthermore, we used the SNP markers to create SNP pairs and performed genomic prediction with the SNP pairs instead of the single SNPs. Finally, we used the information about the variable importance of each single SNP to create SNP pairs with only the best SNP markers and selected the optimal set of SNPs for genomic prediction with SNP pairs. We provide an R script as well as the data from this trial to encourage researchers to perform feature selection with SNP pairs in their studies. The R script as well as the data from this trial have been published in version v1.0 at https://github.com/tmlange/IFS\_SNPpairs.git.⁴³

Methods

Experimental design and data preparation

The greenhouse test was performed with 156 genotypes. For each genotype, 15 plants were grown. Therefore, sugar beet lines were used which were created by crossing two sugar beet lines and self-pollinating the resulting hybrids two times. From the resulting seeds, 15 were chosen from each of the S2 plants as seeds for this trial and the genotype of the parent was assumed as the genotype of each of the seedlings. Thus, the parent was analysed using a SNP chip and the genomic data were used for the descendants. From the 156 genotypes that were used in this trial, 155 genotypes carried the resistance at the two known genes in homozygous form. Thus, it can be assumed that the descendants from these plants must carry the resistance in a homozygous form as well. One genotype, however, was susceptible at Rz2. Also here, it can be assumed that the descendants from this plant must be susceptible in a homozygous form.

Plants were grown for ten weeks in the greenhouse in soil infested with BNYVV, pathotype P. This variant of BNYVV contains five RNA strands⁴⁴ and is, thus, assumed to be more aggressive than the variants with four RNA strands.¹⁷ After ten weeks, plants were removed from the soil and plant sap from lateral roots was extracted. Afterwards, the optical density (OD) value of each sample was measured using the double antibody sandwich enzyme-linked immunosorbent assay (DAS-ELISA). The OD values were measured after 60 minutes, 90 minutes, and 120 minutes using the Infinite F50® (Tecan Group AG, Männedorf, Switzerland) at a wavelength of 405 nm. Harvest, sample preparation and conduction of the DAS-ELISA test followed the protocol described in.⁴⁵

Although DAS-ELISA is an often used tool to measure the concentration of BNYVV in samples from sugar beet,⁷^,¹⁰^,²³ it does not directly measure the virus concentration in form of the OD values.⁴⁶ To estimate the virus concentrations from the raw OD values as well as to reduce measurement errors for each 96-well plate, we transformed the non-normally distributed raw data to normally distributed data with an inverse logistic regression model.⁴⁷ Therefore, a logistic regression model was derived using a serial dilution with 12 samples on each 96-well plate. The transformation followed the protocol in Ref. 47 with one adjustment: The ODs were not only measured after 90 minutes but also after 60 and 120 minutes. Thus, each sample had three OD measurements and three transformed measurements. As described in Ref. 47, it can be assumed that the transformed data are normally distributed. Thus, the mean of the transformed data has been calculated and used as response variable to reduce technical errors during measurement at each time point. A statistical model was fit to the data points in the serial dilution and, subsequently, OD values were transformed according to equation 1:

(1)

\begin{array}{l} {\hat{OD}}_{i} = \tilde{bc} + \frac{tl - \tilde{bc}}{{[1 + 2^{S \cdot (ld (I) - ld (C_{i}))}]}^{A}} \\ ld (\hat{C_{i}}) = ld (\frac{I}{{[{(\frac{tl - \tilde{bc}}{{OD}_{i} - \tilde{bc}})}^{\frac{1}{A}} - 1]}^{\frac{1}{S}}}) \end{array}

with

{OD}_{i}

being the OD value of sample

i

C_{i}

being the virus concentration of sample

i

\tilde{bc}

being the median of the buffer controls on each 96-well plate,

tl

being the technical limit of the machine,

A

describing the asymmetry of the curve,

I

being the relative virus concentration (

C_{i}

) at the inflection point if

A = 1

, and

S

being the slope at the inflection point. Both

A

and

S

can be set freely with the lower limit of zero.

After the data set was transformed, the mean of the transformed data was calculated for all plants which were descendants of the same parent. Thus, if no plants died during the trial, the mean from 15 plants was calculated as the phenotypic data point for the corresponding genotype.

After transformation and calculating the mean of the transformed values, the SNPs were prepared. For this, SNPs with missing values were removed from the data set. Moreover, redundant SNPs were removed through linkage disequilibrium pruning. In this step, one of two SNPs that were correlated with more than an $r^{2}$ of $0.95$ was removed. This step should ensure that epistasis results were not confounded by linkage disequilibrium.³²^,⁴⁸ Furthermore, SNPs with a major allele frequency of 0.95 or higher were removed. After the final step of SNP filtering, 9,127 SNPs were kept in the data set. Furthermore, since only one of the 155 genotypes was susceptible at Rz2, it can be assumed that the SNPs in high linkage disequilibrium with Rz2 must have been removed in the last step of filtering.

Finally, the remaining SNPs were recoded as 0 (homozygous major allele), 2 (homozygous minor allele), and 1 (heterozygous). This kind of coding was recommended for analysing genotypic and additive genetic models.⁴⁹ All filtering steps and the recoding of the SNPs were performed using PLINK v1.90b6.10.⁵⁰

Genomic prediction and feature selection using single SNPs

After data were prepared, genomic prediction was performed using single SNPs. Therefore, the data set was divided randomly into 80% training data (125 data points) and 20% test data (31 data points). Following the experimental design in other studies that used feature selection,⁵¹ this process was repeated 10 times. Subsequently, genomic prediction was performed using random forest. To do so, the R package ranger, version 0.14.1 was used with default settings.⁵²

Prediction accuracy was evaluated by prediction of the test data set with a prediction model that was derived using the training data set. Subsequently, the coefficient of determination ( $R^{2}$ ) was used to compare the predicted values to the observed values in the test data set. The coefficient of determination is defined as the proportion of the explained variability of the total variability⁵³ and was used in previous studies as measure for the prediction accuracy.⁵⁴^,⁵⁵

To perform feature selection, the variable importance of each SNP was estimated using random forest in a first step. Therefore, the R package Boruta, version 7.0.0 was used.⁵⁶ The R function Boruta from this package performs multiple random forest runs with the given input data and calculates multiple quantities as the resulting variable importance per input variable. This function was used in previous studies to assess the variable importance of SNPs.⁵⁴^,⁵⁷^,⁵⁸ We chose the mean variable importance as estimate of the variable importance per SNP. We used a confidence level of $10^{- 10}$ , 2,000 trees and 200 as the maximum number of runs.

After the variable importance per SNP was estimated, feature selection was performed by carrying out genomic prediction with a random forest model that contained only the two SNPs with the highest variable importance. Subsequently, genomic prediction was performed using the three best SNPs, and so on. For each number of SNPs in the prediction model, the prediction accuracy as explained above was calculated. Since random forest can lead to different results in prediction accuracy even if the same data were used as training and test data set, prediction accuracy was estimated as the median prediction accuracy from ten repetitions. To prevent over-optimistic values for the prediction accuracy, variable importance was only estimated using the training data set.⁵⁹ In this way, genomic prediction using feature selection can be compared to genomic prediction using all available SNPs.⁵¹^,⁶⁰

Performing the feature selection method as described above led to a variable importance per SNP as well as a prediction accuracy for each prediction model containing the $i$ best SNPs for each of the ten random splits of the data set. In a next step, the prediction accuracy for each number of SNPs was defined as the median from these ten repetitions. Subsequently, the optimal number of SNPs was defined as the number of SNPs that maximised the median prediction accuracy from the ten repetitions.

Genomic prediction and feature selection using SNP pairs

Besides genomic prediction with single SNPs, genomic prediction was also performed using SNP pairs. Since the genomic data set contained 9,127 SNPs after the data preparation and filtering, theoretically more than 41 million SNP pairs could be created out of these single SNPs. To reduce the resulting data set to a size that a computer can handle, PLINK’s epistasis test was performed using default settings. In this way, the interaction term of each two SNPs is tested for significance at a significance threshold of $α = 0.0001$ .⁶¹ The selection of SNP pairs was performed with each training data set individually to prevent bias during the selection process.

After the SNP pairs were selected using PLINK’s epistasis test, the genotype of each SNP pair was defined using an additive-additive interaction model. In this way, the genotype of each SNP pair was defined as the product of both single SNPs.⁴⁹ Thus, if any of the single SNPs was homozygous for the major allele (coded as 0 in the single SNPs), the genotype of the SNP pair was defined as 0. This was the case for five of the nine possible genotypes of a SNP pair. The combination of two heterozygous single SNPs would lead to a 1 for the SNP pair, the combination of a heterozygous SNP with a SNP that provides a homozygous minor allele would be 2, and the combination of two SNPs that provide homozygous minor alleles would be 4. The recoding of single SNPs as well as the resulting genotype of the SNP pair is summarised in Table 1.

Table 1. Recoding of two theoretical SNPs as well as the resulting SNP pair according to Ref. 49.

A and B represent major alleles and a and b represent minor alleles for SNP A and SNP B, respectively. The resulting SNP pair corresponds to the product of the single SNPs in an additive-additive SNP-interaction model.

Genotypes	Coding for SNP A	Coding for SNP B	Coding for SNP pair
AA/BB	0	0	0
AA/Bb	0	1	0
AA/bb	0	2	0
Aa/BB	1	0	0
Aa/Bb	1	1	1
Aa/bb	1	2	2
aa/BB	2	0	0
aa/Bb	2	1	2
aa/bb	2	2	4

After the SNP pairs were recoded, genomic prediction was performed with all SNP pairs that were selected from each training data set. Therefore, a prediction model was derived using random forest with each training data set (as described above with the ranger function with default settings), the phenotypic values of the corresponding test data set were predicted with the prediction model, and prediction accuracy was estimated as $R^{2}$ between the predicted and the observed values.

However, since PLINK’s epistasis test is based on linear regression and random forest is a method from machine learning, we developed an alternative for selecting SNP pairs from single SNPs based on machine learning methods. Therefore, we used the information about the variable importance of each single SNP as it was provided by the Boruta function and combined the single SNPs with the highest variable importance to all possible SNP pairs. Subsequently, genomic prediction was performed using all SNP pairs created with the best single SNPs and the resulting prediction accuracy was stored. This process was repeated for the three to 200 single SNPs with the highest variable importance. Finally, the number of single SNPs was determined where the resulting SNP pairs maximised the prediction accuracy. As with the other methods, this method was repeated with each training data set individually to avoid bias and afterwards the median from the ten repetitions was calculated for each number of analysed SNPs. An R script as well as the data from this trial are provided at https://github.com/tmlange/IFS\_SNPpairs.git⁴³ to give researchers the possibility to perform feature selection with SNP pairs based on the variable importance of single SNPs.

Results

The 155 genotypes which carry both known resistances provided raw OD values measured after 90 minutes in the range from 0.1107 to 4 which is the technical limit of the machine. The transformed data were in the range from -7.06 to 12.33. These results show the highest possible variation of virus concentrations that the machine can measure. Thus, although these genotypes were assumed to be resistant at the two known resistance clusters, the resulting data set provides sufficient variance of the resistance levels to perform genomic prediction.

Genomic prediction and feature selection using single SNPs

First, genomic prediction was performed using all 9,127 single SNPs that were left after filtering. Performing genomic prediction with the single SNPs with the ten random splits of the data set resulted in a median prediction accuracy of $R^{2} = 0.146$ . The median prediction accuracies resulting from genomic prediction using any of the methods described can be seen in Table 2.

Table 2. Prediction accuracy as median of $R^{2}$ from the ten repetitions with each of the four methods: Using all single SNPs that were left after filtering, using the 29 SNPs that were assumed to be the optimal subset after feature selection, using all SNP pairs that were left after selection via PLINK’s epistasis test, and using the SNP pairs that result from including the 16 single SNPs with the highest variable importance.

Method	Single SNPs	SNP pairs
All variables after filtering	0.146	0.191
Subset after feature selection	0.267	0.306

Next to genomic prediction with all SNPs that were left after filtering, incremental feature selection was performed to optimise prediction accuracy by selecting a subset of optimal SNPs for genomic prediction. Therefore, Boruta was performed to estimate the variable importance of each SNP. To prevent bias in the data analysis, this analysis was performed in each training data set individually. Subsequently, genomic prediction was performed using random forest.

After performing this analysis, each number of SNPs and the corresponding prediction accuracy was retrieved for each of the ten splits between training and test data set. Figure 1 shows the number of SNPs in the prediction model on the X axis and the corresponding prediction accuracy as the median of the prediction accuracy from the ten repetitions on the Y axis. One can see that the prediction accuracy increases steeply when the first SNPs are included in the prediction model. However, slightly above $R^{2} = 0.25$ , the prediction accuracy forms a peak and decreases from there on with the decrease being less steep than the increase at the beginning of the curve.

Figure 1. Median of the $R^{2}$ values from the ten repetitions of genomic prediction using random forest with the 2, $\dots$ , 9,127 SNPs.

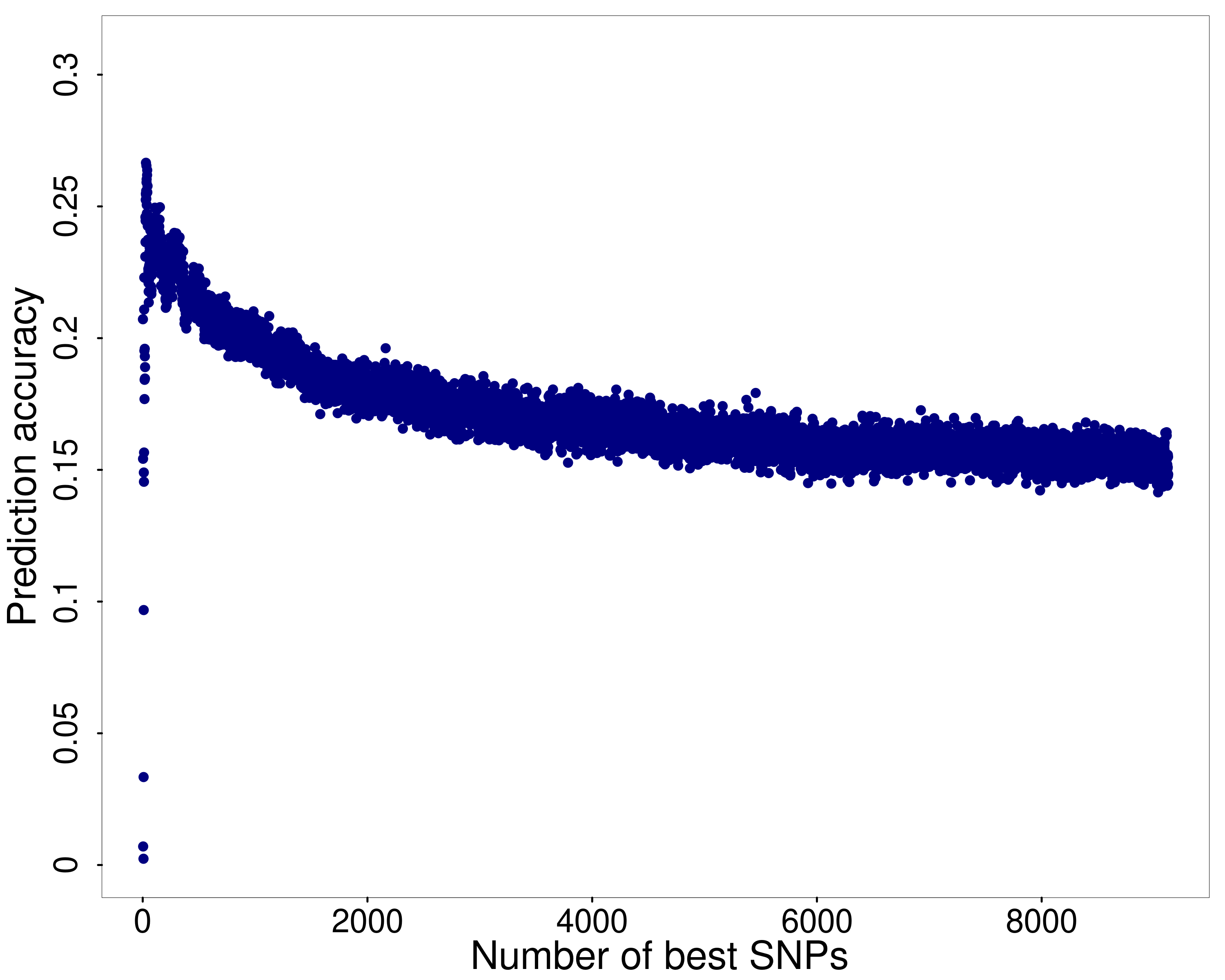
In this way, the optimal set of SNPs for genomic prediction was determined. Thus, the number of SNPs was selected that maximised the median of the prediction accuracy from the ten repetitions. Here, the prediction accuracy maximised if 29 SNPs were included in the prediction model. This resulted in a median prediction accuracy of $R^{2} = 0.267$ . However, we found that within the ten training data sets, not all 29 SNPs were the same.

Genomic prediction and feature selection using SNP pairs

Besides genomic prediction and feature selection with single SNPs, similar approaches have been performed using SNP pairs. To perform genomic prediction with SNP pairs, PLINK’s epistasis test was performed with default settings for each training data set individually. After filtering via PLINK’s epistasis test, only SNP pairs were kept in the data set whose interaction term in a linear regression model led to a $p$ value below the default threshold of 0.0001. The resulting sample sizes resulted in 46,556 to 87,529 SNP pairs. Taking the 41 million theoretically possible SNP pairs into consideration, this is a reduction to 0.1% to 0.2%. When genomic prediction was performed with all SNP pairs that were left after filtering using PLINK’s epistasis test with each training set, the median prediction accuracy was $R^{2} = 0.191$ .

Besides genomic prediction with all SNP pairs that were left after filtering with PLINK’s epistasis test, feature selection was performed to analyse an optimal subset of SNP pairs for genomic prediction. Therefore, the best single SNPs judged by their variable importance were selected and used to create SNP pairs as described in Table 1. Subsequently, genomic prediction was performed using random forest with the SNP pairs that resulted from the 3, $\dots$ , 200 best single SNPs. Figure 2 displays the median prediction accuracy from the ten repetitions on the Y axis and the corresponding number of single SNPs that make up the SNP pairs on the X axis.

Figure 2. Median of the $R^{2}$ values from the ten repetitions of genomic prediction using random forest when the 3, $\dots$ , 200 best single SNPs are combined to SNP pairs.

One can see that the prediction accuracy increases steeply when a small number of SNP pairs are included in the prediction model. Similar to Figure 1 that displays the prediction accuracy with the single SNPs, the prediction accuracy with the SNP pairs also forms a peak and decreases from there on. One can see that the peak height is slightly above $R^{2} = 0.3$ when SNP pairs are created using the 16 best SNPs.

Considering Figure 2, one can assume that the number of SNP pairs has an effect on the resulting prediction accuracy. Thus, one could assume that the prediction accuracy could be affected by the number of SNP pairs that is selected via PLINK’s epistasis test. Therefore, we have analysed how many SNP pairs were selected via PLINK if the significance threshold was modified. Naturally, the number of selected SNP pairs was reduced if the threshold was decreased and conversely, more SNP pairs were left after filtering if the threshold was increased. However, if subsequently all selected SNP pairs were used for genomic prediction, the resulting prediction accuracy did not seem to be affected (tested for thresholds $10^{- 2}$ , $\dots$ , $10^{- 8}$ , data not shown). Thus, we conclude that although the number of selected SNP pairs can be easily adjusted in PLINK’s epistasis test, this selection did not affect the resulting prediction accuracy for this data set.

Discussion

Although rhizomania resistance was assumed to be a quantitative trait caused by major and minor resistance genes,¹⁸ to date no attempt of genomic prediction of rhizomania resistance has been performed. We provide a first attempt at predicting the resistance of sugar beet genotypes against rhizomania. To do so, we used a sugar beet population where each genotpye can be assumed to be resistant at Rz1. Furthermore, 155 of the 156 genotypes can be assumed to be resistant at Rz2. Thus, all SNPs in high linkage disequilibrium with either Rz1 or Rz2 should have been removed during SNP pruning. However, the results show that genomic prediction of rhizomania resistance was still possible. In this way, we provide evidence that the genomic architecture of rhizomania resistance is most probably caused by more than two resistance clusters.

To perform genomic prediction, we split the data set ten times randomly into subsets of 80% training data and 20% test data. Performing genomic prediction with all available SNP markers led to a median prediction accuracy of $R^{2} = 0.146$ . Moreover, we performed feature selection using methods from machine learning to reduce the number of SNPs in the prediction model to an optimal subset. This method led to a median prediction accuracy of $R^{2} = 0.267$ when only the 29 best SNPs were included in the prediction model.

Previous studies of variable importance in genomic prediction have concluded that although SNP interactions can be detected in random forest algorithms, such interactions can be masked by other variables when working with high-dimensional data.⁶²^,⁶³ Thus, it could be assumed that SNP interactions are masked when genomic prediction was performed with all single SNPs. Consequently, when the number of SNPs was reduced, SNP interactions were not masked and could be included in the prediction model more efficiently.

Besides genomic prediction using single SNPs, we also present results from genomic prediction using SNP pairs. For this, single SNPs were combined to pairs and the theoretical number of resulting SNP pairs was reduced using PLINK’s epistasis test. Performing genomic prediction with all SNP pairs that were left after filtering resulted in a median prediction accuracy of $R^{2} = 0.191$ .

Finally, we used the information about variable importance of each SNP to perform feature selection also with the SNP pairs. Therefore, SNP pairs were created using only the 3, $\dots$ , 200 single SNPs with the highest variable importance and the corresponding prediction accuracy was estimated. This new approach allowed us to perform incremental feature selection using machine learning with SNP pairs. Similar to feature selection with single SNPs, the prediction accuracy for the SNP pairs was maximised if only a certain number of SNP pairs was included in the prediction model. Here, the prediction accuracy was maximised if the prediction model contained SNP pairs from the 16 best single SNPs. This method led to a median prediction accuracy of $R^{2} = 0.306$ which was the highest prediction accuracy from all four methods under investigation. These results might indicate that rhizomania is affected by interactions between SNP pairs which are also masked if all SNP pairs are included in the prediction model. Consequently, it might be assumed that not only epistatic effects caused by two genes but also by multiple genes could play a role in rhizomania resistance.

Feature selection was used in recent studies to increase the prediction accuracy of genomic prediction models in man⁵⁹ and crops.⁵¹^,⁵⁴ However, these studies led to heterogeneous results such that no general recommendation can be given regarding feature selection. Here, we show that in case of rhizomania resistance, prediction accuracy could be increased using feature selection. We postulate that the success of implementing feature selection to improve prediction accuracy might be related to epistatic effects that are masked if a large number of SNPs are included in a prediction model. However, we assume the present study alone is not sufficient to underpin this hypothesis. Thus, further research is necessary to study the role of SNP interactions in rhizomania resistance as well as the possibility to improve genomic prediction via feature selection.

Besides improving prediction accuracy of genomic prediction models, other studies used results from feature selection via genomic prediction to determine the association between certain SNPs and the phenotype.⁵⁴^,⁶⁴ Following this approach, it could be interesting to use the method presented here to select the 29 single SNPs or the 16 SNP pairs, respectively, as being associated with rhizomania resistance. However, we found that the estimation of variable importance did not lead to the same results in each training data set. Consequently, the SNP pairs differed for each training data set as well. Thus, we conclude that the present method can be useful to increase the prediction accuracy of prediction models but is not useful to select certain SNPs or SNP pairs as being associated with the phenotype.

Conclusions

Here, we present a first attempt at genomic prediction of rhizomania resistance in sugar beet. Therefore, we used a sugar beet population with 156 genotypes of which all genotypes can be assumed to be resistant at Rz1 and 155 genotypes can be assumed to be resistant at Rz2. The 155 genotypes that were resistant at Rz2, provided the highest possible variation of virus concentrations that the machine can measure. Moreover, although SNPs in high linkage disequilibrium with Rz1 and Rz2 were removed during SNP pruning, genomic prediction was possible with the genomic data. If rhizomania resistance was caused only by the two known resistance clusters, this should not be the case.

To perform genomic prediction, we have used single SNPs as well as SNP pairs. In the provided data set, the genomic prediction using SNP pairs led to higher prediction accuracy than the genomic prediction using single SNPs. These results lead to the conclusion that epistatic effects might affect rhizomania resistance and that the usage of SNP pairs can include these effects more efficiently in the prediction model.

Moreover, we have shown that a selection of the “best” SNPs increased prediction accuracy even further. It was concluded in former studies that although random forest can detect SNP interactions, such interactions can be masked by other variables in high-dimensional data.⁶²^,⁶³ In this way, our results fit to the conclusions from these studies since the prediction accuracy was increased if only a subset of all available SNPs was used for genomic prediction. Moreover, our results indicate that the variable importance that was estimated using Boruta, hence, random forest, also included information about SNP interactions. Thus, we conclude that a reduction of the SNP number via the variable importance enables the random forest algorithm to incorporate SNP interactions better into the prediction model.

Furthermore, we have also performed feature selection with the SNP pairs to reduce the data set to a certain subset of optimal SNP pairs. The inclusion of a subset of SNP pairs in the prediction model increased the prediction accuracy compared to the prediction model that included all SNP pairs that were left after filtering via PLINK’s epistasis test. Following the conclusion with the single SNPs, this might indicate that rhizomania resistance is caused by interactions of more than two genes and that the interaction of SNP pairs might be similarly masked if a large number of SNP pairs is included in the prediction model.

All in all, the optimisation of the prediction model increased the median prediction accuracy with the ten repetitions that are provided here. These results make us assume that rhizomania resistance could be caused by a multitude of genes which interact and that the implementation of such interactions in a prediction model can increase prediction accuracy. However, further research in this regard is necessary. To encourage researchers to perform feature selection with SNP pairs in their own studies, we have published an R script as well as the data from this trial at https://github.com/tmlange/IFS_SNPpairs.git.⁴³

Data availability

Underlying data

Zenodo: IFS_SNPpairs v1.0, https://doi.org/10.5281/zenodo.7624425.⁴³

This project contains the following underlying data:

• TestData.csv
• TrainingData.csv

Data are available under the terms of the Creative Commons Zero “No rights reserved” data waiver (CC0 1.0 Public domain dedication).

Extended data

Analysis code

Analysis code available from: https://github.com/tmlange/IFS_SNPpairs.git

Archived analysis code at time of publication: https://doi.org/10.5281/zenodo.7624425.⁴³

License: MIT

Acknowledgements

We acknowledge support by the Open Access Publication Funds of the Göttingen University. Furthermore, we would like to thank the Phytopathology group of KWS SAAT SE & Co. KGaA for performing the greenhouse trial and laboratory work.

References

1. Řezbová H, Belová A, Škubna O: Sugar beet production in the European Union and their future trends. Agris on-line Papers in Economics and Informatics. 2013; 5(665-2016-44967): 165–178.
2. Draycott AP: Sugar Beet. 1st ed.New York: John Wiley & Sons; 2008. 978-1-405-17336-0.
3. Scholten OE, Lange W: Breeding for resistance to rhizomania in sugar beet: A review. Euphytica. 2000; 112(3): 219–231. Publisher Full Text
4. Tamada T: Beet necrotic yellow vein virus. CMI/AAB Description of plant viruses. 1975; 144: 1–4.
5. Giunchedi L, Giuchedi L, Langenberg WG: Beet necrotic yellow vein virus transmission by Polymyxa betae keskin zoospores. Phytopathol. Mediterr. 1982;5–7.
6. Ciafardini G: Evaluation of Polymyxa betae Keskin contaminated by Beet necrotic yellow vein virus in soil. Appl. Environ. Microbiol. 1991; 57(6): 1817–1821. PubMed Abstract | Publisher Full Text | Free Full Text
7. Özmen CY, Khabbazi SD, Khabbazi AD, et al.: Genome composition analysis of multipartite BNYVV reveals the occurrence of genetic re-assortment in the isolates of Asia Minor and Thrace. Sci. Rep. 2020; 10(1): 4111–4129. PubMed Abstract | Publisher Full Text | Free Full Text
8. Abe H, Tamada T: Association of beet necrotic yellow vein virus with isolates of Polymyxa betae Keskin. Japanese Journal of Phytopathology. 1986; 52(2): 235–247. Publisher Full Text
9. Biancardi E, Tamada T: Rhizomania. Springer International Publishing; 2016. Publisher Full Text
10. Broccanello C, McGrath JM, Panella L, et al.: A SNP mutation affects rhizomania-virus content of sugar beets grown on resistance-breaking soils. Euphytica. 2017; 214(1). Publisher Full Text
11. European Food Safety Authority (EFSA) Panel on Plant Health (PLH)Dehnen-Schmutz K, Di Serio F, et al.: Pest categorisation of beet necrotic yellow vein virus. EFSA J. 2020; 18(12). 18314732. Publisher Full Text
12. McGrann GRD, Grimmer MK, Mutasa-Göttgens ES, et al.: Progress towards the understanding and control of sugar beet rhizomania disease. Mol. Plant Pathol. 2009; 10(1): 129–141. PubMed Abstract | Publisher Full Text | Free Full Text
13. Koenig R, Lüddecke P, Haeberle AM: Detection of beet necrotic yellow vein virus strains, variants and mixed infections by examining single-strand conformation polymorphisms of immunocapture RT-PCR products. J. Gen. Virol. 1995; 76(8): 2051–2055. PubMed Abstract | Publisher Full Text
14. Tamada T, Shirako Y, Abe H, et al.: Production and pathogenicity of isolates of beet necrotic yellow vein virus with different numbers of rna components. J. Gen. Virol. 1989; 70(12): 3399–3409. Publisher Full Text
15. Harju VA, Mumford RA, Blockley A, et al.: The occurrence in the United Kingdom of Beet necrotic yellow vein virus isolates which contain RNA 5. New Dis. Rep. 2002; 51: 18–18. Publisher Full Text
16. Koenig R, Lennefors B-L: Molecular analyses of European A, B and P type sources of Beet necrotic yellow vein virus and detection of the rare P type in Kazakhstan. Arch. Virol. 2000; 145(8): 1561–1570. PubMed Abstract | Publisher Full Text
17. Heijbroek W, Musters PMS, Schoone AHL: Variation in pathogenicity and multiplication of beet necrotic yellow vein virus (BNYVV) in relation to the resistance of sugar-beet cultivars. Eur. J. Plant Pathol. 1999; 105(4): 397–405. Publisher Full Text
18. De Biaggi M, Stevanato P, Saccomani M, et al.: Sugar beet resistance to rhizomania: State of the art and perspectives. Sugar Tech. 2010; 12(3-4): 238–242. Publisher Full Text
19. De Biaggi M: Methodes de delection-un cas concret. Proceedings of IIBR 50th Winter Congress, 1987. Institut International de Recherches Betteravieres; 1987.
20. Lewellen RT, Skoyen IO, Erichsen AW: Breeding sugar beet for resistance to rhizomania: Evaluation of host-plant reactions and selection for and inheritance of resistance. 50. Winter Congress of the International Institute for Sugar Beet Research, Bruxelles (Belgium), 11-12 Feb. 1987. IIRB. Secretariat General. 1987.
21. Stevanato P, De Biaggi M, Broccanello C, et al.: Molecular genotyping of “rizor” and “holly” rhizomania resistances in sugar beet. Euphytica. 2015; 206(2): 427–431. Publisher Full Text
22. Scholten OE, De Bock TSM, Klein-Lankhorst RM, et al.: Inheritance of resistance to beet necrotic yellow vein virus in Beta vulgaris conferred by a second gene for resistance. Theor. Appl. Genet. 1999; 99(3-4): 740–746. PubMed Abstract | Publisher Full Text
23. Capistrano-Gossmann GG, Ries D, Holtgräwe D, et al.: Crop wild relative populations of Beta vulgaris allow direct mapping of agronomically important genes. Nat. Commun. 2017; 8(1): 1–8.
24. Gidner S, Lennefors B-L, Nilsson N-O, et al.: QTL mapping of BNYVV resistance from the WB41 source in sugar beet. Genome. 2005; 48(2): 279–285. PubMed Abstract | Publisher Full Text
25. Grimmer MK, Trybush S, Hanley S, et al.: An anchored linkage map for sugar beet based on AFLP, SNP and RAPD markers and QTL mapping of a new source of resistance to Beet necrotic yellow vein virus. Theor. Appl. Genet. 2007; 114(7): 1151–1160. February. PubMed Abstract | Publisher Full Text
26. Grimmer MK, Kraft T, Francis SA, et al.: QTL mapping of BNYVV resistance from the WB258 source in sugar beet. Plant Breed. 2008; 127(6): 650–652. Publisher Full Text
27. Lein JC, Asbach K, Tian Y, et al.: Resistance gene analogues are clustered on chromosome 3 of sugar beet and cosegregate with QTL for rhizomania resistance. Genome. 2006; 50(1): 61–71. Publisher Full Text
28. Olatoye MO, Hu Z, Aikpokpodion PO: Epistasis detection and modeling for genomic selection in cowpea (Vigna unguiculata L. Walp.). Front. Genet. 2019; 10: 677. PubMed Abstract | Publisher Full Text | Free Full Text
29. Cordell HJ: Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002; 11(20): 2463–2468. PubMed Abstract | Publisher Full Text
30. Mathew B, Léon J, Sannemann W, et al.: Detection of epistasis for flowering time using bayesian multilocus estimation in a barley MAGIC population. Genetics. 2018; 208(2): 525–536. PubMed Abstract | Publisher Full Text | Free Full Text
31. Carlborg Ö, Haley CS: Epistasis: too often neglected in complex trait studies?. Nat. Rev. Genet. 2004; 5(8): 618–625. PubMed Abstract | Publisher Full Text
32. Heinrich F, Ramzan F, Rajavel A, et al.: MIDESP: Mutual Information-Based Detection of Epistatic SNP Pairs for Qualitative and Quantitative Phenotypes. Biology. 2021; 10(9): 921. PubMed Abstract | Publisher Full Text | Free Full Text
33. Würschum T, Maurer HP, Schulz B, et al.: Genome-wide association mapping reveals epistasis and genetic interaction networks in sugar beet. Theor. Appl. Genet. 2011; 123(1): 109–118. PubMed Abstract | Publisher Full Text
34. Poland JA, Balint-Kurti PJ, Wisser RJ, et al.: Shades of gray: the world of quantitative disease resistance. Trends Plant Sci. 2009; 14(1): 21–29. PubMed Abstract | Publisher Full Text
35. St DA, Clair: Quantitative disease resistance and quantitative resistance loci in breeding. Annu. Rev. Phytopathol. 2010; 48: 247–268. Publisher Full Text
36. Bao Y, Vuong T, Meinhardt C, et al.: Potential of association mapping and genomic selection to explore pi 88788 derived soybean cyst nematode resistance. Plant Genome. 2014; 7(3). plantgenome2013–11. Publisher Full Text
37. Tiede T, Smith KP: Evaluation and retrospective optimization of genomic selection for yield and disease resistance in spring barley. Mol. Breed. 2018; 38(5): 1–16. Publisher Full Text
38. Roy J, Shaikh TM, del Río Mendoza L , et al.: Genome-wide association mapping and genomic prediction for adult stage sclerotinia stem rot resistance in brassica napus (l) under field environments. Sci. Rep. 2021; 11(1): 1–18. Publisher Full Text
39. Huang M, Balimponya EG, Mgonja EM, et al.: Use of genomic selection in breeding rice (Oryza sativa L.) for resistance to rice blast (magnaporthe oryzae). Mol. Breed. 2019; 39(8): 1–16. Publisher Full Text
40. Tomar V, Singh Dhillon G, Singh D, et al.: Evaluations of genomic prediction and identification of new loci for resistance to stripe rust disease in wheat (Triticum aestivum L.). Front. Genet. 2021; 12. PubMed Abstract | Publisher Full Text | Free Full Text
41. Ornella L, Pérez P, Tapia E, et al.: Genomic-enabled prediction with classification algorithms. Heredity. 2014; 112(6): 616–626. PubMed Abstract | Publisher Full Text | Free Full Text
42. González-Camacho JM, Ornella L, Pérez-Rodríguez P, et al.: Applications of machine learning methods to genomic selection in breeding wheat for rust resistance. Plant Genome. 2018; 11(2): 170104. PubMed Abstract | Publisher Full Text
43. Lange TM: IFS_SNPpairs.Feb 2023. Reference Source
44. Schirmer A, Link D, Cognat V, et al.: Phylogenetic analysis of isolates of Beet necrotic yellow vein virus collected worldwide. J. Gen. Virol. 2005; 86(10): 2897–2911. PubMed Abstract | Publisher Full Text
45. Lange TM, Wutke M, Bertram L, et al.: Decision Strategies for Absorbance Readings from an Enzyme-Linked Immunosorbent Assay—A Case Study about Testing Genotypes of Sugar Beet (Beta vulgaris L.) for Resistance against Beet necrotic yellow vein virus (BNYVV). Agriculture. 2021; 11(10): 956. Publisher Full Text
46. Clark MF, Adams AN: Characteristics of the microplate method of enzyme-linked immunosorbent assay for the detection of plant viruses. J. Gen. Virol. 1977; 34(3): 475–483. PubMed Abstract | Publisher Full Text
47. Lange TM, Rotärmel M, Müller D, et al.: Non-linear transformation of enzyme-linked immunosorbent assay (ELISA) measurements allows usage of linear models for data analysis. Virol. J. 2022; 19(1): 1–11. Publisher Full Text
48. Joiret M, Mahachie John JM, Gusareva ES, et al.: Confounding of linkage disequilibrium patterns in large scale DNA based gene-gene interaction studies. BioData Min. 2019; 12(1): 1–23. Publisher Full Text
49. Hartwig FP: SNP-SNP Interactions: focusing on variable coding for complex models of epistasis. J. Genet. Syndr. Gene Ther. 2013; 4(189): 10–4172.
50. Purcell S, Neale B, Todd-Brown K, et al.: PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007; 81(3): 559–575. PubMed Abstract | Publisher Full Text | Free Full Text
51. Azodi CB, Bolger E, McCarren A, et al.: Benchmarking parametric and machine learning models for genomic prediction of complex traits. G3: Genes, Genomes, Genetics. 2019; 9(11): 3691–3702. PubMed Abstract | Publisher Full Text | Free Full Text
52. Wright MN, Ziegler A: ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017; 77(1): 1–17. Publisher Full Text
53. Renaud O, Victoria-Feser M-P: A robust coefficient of determination for regression. J. Stat. Plan. Inference. 2010; 140(7): 1852–1862. Publisher Full Text
54. Haleem A, Klees S, Schmitt AO, et al.: Deciphering pleiotropic signatures of regulatory SNPs in Zea mays L. using multi-omics data and machine learning algorithms. Int. J. Mol. Sci. 2022; 23(9): 5121. PubMed Abstract | Publisher Full Text | Free Full Text
55. Segelke D, Chen J, Liu Z, et al.: Reliability of genomic prediction for German Holsteins using imputed genotypes from low-density chips. J. Dairy Sci. 2012; 95(9): 5403–5411. PubMed Abstract | Publisher Full Text
56. Kursa MB, Rudnicki WR: Feature selection with the Boruta package. J. Stat. Softw. 2010; 36: 1–13. Publisher Full Text
57. Ramzan F, Klees S, Schmitt AO, et al.: Identification of Age-Specific and Common Key Regulatory Mechanisms Governing Eggshell Strength in Chicken using Random Forests. Gen. 2020; 11(4): 464. Publisher Full Text
58. Klees S, Lange TM, Bertram H, et al.: In silico identification of the complex interplay between regulatory snps, transcription factors, and their related genes in brassica napus l. using multi-omics data. Int. J. Mol. Sci. 2021; 22(2): 789. PubMed Abstract | Publisher Full Text | Free Full Text
59. Bermingham ML, Pong-Wong R, Spiliopoulou A, et al.: Application of high-dimensional feature selection: evaluation for genomic prediction in man. Sci. Rep. 2015; 5(1): 1–12.
60. Sirsat MS, Oblessuc PR, Ramiro RS: Genomic prediction of wheat grain yield using machine learning. Agriculture. 2022; 12(9): 1406. Publisher Full Text
61. Chang C: Epistasis test - plink 1.9. Retrieved March 01, 2022, 2022. Reference Source
62. Winham SJ, Colby CL, Freimuth RR, et al.: SNP interaction detection with random forests in high-dimensional genetic data. BMC bioinformatics. 2012; 13(1): 1–13. Publisher Full Text
63. Wright MN, Ziegler A, König IR: Do little interactions get lost in dark random forests? BMC bioinformatics. 2016; 17(1): 1–10. Publisher Full Text
64. Shikha M, Kanika A, Rao AR, et al.: Genomic selection for drought tolerance using genome-wide snps in maize. Front. Plant Sci. 2017; 8: 550. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 14 Mar 2023

Author details Author details

Thomas Martin Lange
Roles: Formal Analysis, Investigation, Methodology, Software, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Felix Heinrich
Roles: Formal Analysis, Methodology, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Friedrich Kopisch-Obuch
Roles: Investigation, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Harald Keunecke
Roles: Investigation, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

Mehmet Gültas
Roles: Conceptualization, Investigation, Methodology, Project Administration, Supervision, Validation, Writing – Review & Editing

Armin O. Schmitt
Roles: Conceptualization, Investigation, Methodology, Project Administration, Resources, Supervision, Validation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 28 Aug 2024, 12:280

https://doi.org/10.12688/f1000research.131134.2

version 1

Published: 14 Mar 2023, 12:280

https://doi.org/10.12688/f1000research.131134.1

© 2023 Lange TM et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Lange TM, Heinrich F, Kopisch-Obuch F et al. Improving genomic prediction of rhizomania resistance in sugar beet (Beta vulgaris L.) by implementing epistatic effects and feature selection [version 1; peer review: 3 not approved]. F1000Research 2023, 12:280 (https://doi.org/10.12688/f1000research.131134.1)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Current Reviewer Status: ?

Key to Reviewer Statuses VIEW HIDE

ApprovedThe paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approvedFundamental flaws in the paper seriously undermine the findings and conclusions

Version 1

VERSION 1

PUBLISHED 14 Mar 2023

Views

Reviewer Report 27 Sep 2023

Daniela Holtgräwe, Genetics and Genomics of Plants, CeBiTec and Faculty of Biology, Bielefeld University, Bielefeld, Germany

Not Approved

https://doi.org/10.5256/f1000research.143945.r196899

The present manuscript deals with genomic prediction of the presumably quantitative trait 'Rhizomania resistance' in sugar beet using genome-wide SNP data. The paper presents bioinformatic and ML-based calculations using all SNPs individually, or in pairs and adding the SNP information step by step.
The pyramiding of sugar beet resistance to rhizomania is of great interest from an agronomic and breeding perspective and is very challenging due to the concentration of the loci on a single chromosome (chr. 3). Medium and large SNP genotyping data sets, such as those used here, are generally well suited for improved prediction of a trait, especially if several genes or gene clusters are involved in the expression of the trait. Not only the aim of the investigations, but also the selection of the sugar beet population and the various bioinformatic methods are interesting and well designed. Nevertheless, the manuscript must be revised with regard to the transparency of the biological material, the data used and the limitations of the results. The revision should present the data in a way so that the results and experiences become more usable for those interested.

Main points:

In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
The programs on github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Plant genetics, crop genomics, computational biology, transcriptomics, genome assembly, gene annotation, RGAs, genetic mapping, genotyping

I confirm that I have read this submission and believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

CITE

Report a concern

Author Response 28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

28 Aug 2024

Author Response

Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At ... Continue reading Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
Author Response:
We agree with the reviewer and have adjusted the introduction based on the recommendations of the reviewer. Furthermore, we have adjusted the Discussion section of the manuscript by adding a short discussion about epistasis and additive effects affecting rhizomania resistance.

Reviewer Comment:
(2) The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
Author Response:
Unfortunately, the rights to the germplasm used in this trial are held by KWS Saat SE & Co. KGaA. We are therefore not in the position to publish this information. However, we have added a data availability statement to the manuscript stating that this information can be shared upon reasonable request.

Reviewer Comment:
(3) For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Author Response:
For the analysis, we have focused on the transformed data that were produced by transforming and averaging the ELISA measurements at all three time points. At the beginning of the results section, however, we have briefly described the OD measurements to show the range of the resulting OD values. Nevertheless, we agree with the reviewer that it is not clear why we have described the range of the OD values measured after 90 minutes and not after 60 and 120 minutes. Thus, we have added the range of the ELISA measurements after 60 and 120 minutes in the manuscript.

Reviewer Comment:
(4) Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
Author Response:
We appreciate the reviewer's criticism and agree that the current version of the manuscript lacked detailed information about the SNPs. Additionally, the reviewer correctly pointed out that, prior to MAF filtering, we are actually considering SNVs, not SNPs. However, we would like to keep referring to the SNVs as SNPs to improve readability of the manuscript since the data were collected using a SNP chip.

Reviewer Comment:
(5) The programs on Github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
Author Response:
We acknowledge the reviewer’s valuable feedback regarding the accessibility of the data from the trial on GitHub. We agree with the criticism and have significantly improved the documentation as requested. This should ensure that the data are now easily accessible and usable.

Reviewer Comment:
(6) In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
Author Response:
This was indeed a typo and we have corrected the corresponding part of the manuscript.

Reviewer Comment:
(7) It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
Author Response:
We have added genotype names for each individual in the data set on GitHub. Furthermore, we have given a special name for the genotype that was susceptible at Rz2 (``Control_susceptibleRz2'').

Reviewer Comment:
(8) For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
Author Response:
We thank the reviewer for this very attentive comment and have adjusted the corresponding part of the manuscript.

Reviewer Comment:
(9) Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
Author Response:
Following the suggestion, we conducted an analysis to assess the overlap of the selected SNPs. Our findings revealed that four SNPs were consistently identified through this approach. Subsequently, we have integrated this information into the manuscript, highlighting that these four detected SNPs account for a significant portion of the total variance in the phenotypic data.

Reviewer Comment:
(10) The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Author Response:
Thanks to the advice of the reviewer to analyse the overlap of selected SNPs, we discovered four SNPs that carry information about rhizomania resistance. In consultation with KWS Saat SE & Co. KGaA, we were allowed to publish the chromosomes on which these four SNPs are located. We show that two of the identified SNPs are not located on chromosome 3 but on chromosomes 2 and 5. We have included this new information in the manuscript which shows the importance of including SNPs from various chromosomes when examining SNP interactions.

Reviewer Comment:
(11) The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.
Author Response:
We appreciate the reviewer's feedback and acknowledge that the manuscript's writing style required enhancement. In response to the reviewer's criticism, we have refined the writing style of the manuscript to reduce redundancy in both the discussion and conclusion sections.
Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
Author Response:
We agree with the reviewer and have adjusted the introduction based on the recommendations of the reviewer. Furthermore, we have adjusted the Discussion section of the manuscript by adding a short discussion about epistasis and additive effects affecting rhizomania resistance.

Reviewer Comment:
(2) The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
Author Response:
Unfortunately, the rights to the germplasm used in this trial are held by KWS Saat SE & Co. KGaA. We are therefore not in the position to publish this information. However, we have added a data availability statement to the manuscript stating that this information can be shared upon reasonable request.

Reviewer Comment:
(3) For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Author Response:
For the analysis, we have focused on the transformed data that were produced by transforming and averaging the ELISA measurements at all three time points. At the beginning of the results section, however, we have briefly described the OD measurements to show the range of the resulting OD values. Nevertheless, we agree with the reviewer that it is not clear why we have described the range of the OD values measured after 90 minutes and not after 60 and 120 minutes. Thus, we have added the range of the ELISA measurements after 60 and 120 minutes in the manuscript.

Reviewer Comment:
(4) Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
Author Response:
We appreciate the reviewer's criticism and agree that the current version of the manuscript lacked detailed information about the SNPs. Additionally, the reviewer correctly pointed out that, prior to MAF filtering, we are actually considering SNVs, not SNPs. However, we would like to keep referring to the SNVs as SNPs to improve readability of the manuscript since the data were collected using a SNP chip.

Reviewer Comment:
(5) The programs on Github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
Author Response:
We acknowledge the reviewer’s valuable feedback regarding the accessibility of the data from the trial on GitHub. We agree with the criticism and have significantly improved the documentation as requested. This should ensure that the data are now easily accessible and usable.

Reviewer Comment:
(6) In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
Author Response:
This was indeed a typo and we have corrected the corresponding part of the manuscript.

Reviewer Comment:
(7) It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
Author Response:
We have added genotype names for each individual in the data set on GitHub. Furthermore, we have given a special name for the genotype that was susceptible at Rz2 (``Control_susceptibleRz2'').

Reviewer Comment:
(8) For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
Author Response:
We thank the reviewer for this very attentive comment and have adjusted the corresponding part of the manuscript.

Reviewer Comment:
(9) Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
Author Response:
Following the suggestion, we conducted an analysis to assess the overlap of the selected SNPs. Our findings revealed that four SNPs were consistently identified through this approach. Subsequently, we have integrated this information into the manuscript, highlighting that these four detected SNPs account for a significant portion of the total variance in the phenotypic data.

Reviewer Comment:
(10) The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Author Response:
Thanks to the advice of the reviewer to analyse the overlap of selected SNPs, we discovered four SNPs that carry information about rhizomania resistance. In consultation with KWS Saat SE & Co. KGaA, we were allowed to publish the chromosomes on which these four SNPs are located. We show that two of the identified SNPs are not located on chromosome 3 but on chromosomes 2 and 5. We have included this new information in the manuscript which shows the importance of including SNPs from various chromosomes when examining SNP interactions.

Reviewer Comment:
(11) The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.
Author Response:
We appreciate the reviewer's feedback and acknowledge that the manuscript's writing style required enhancement. In response to the reviewer's criticism, we have refined the writing style of the manuscript to reduce redundancy in both the discussion and conclusion sections.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

28 Aug 2024

Author Response

Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At ... Continue reading Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
Author Response:
We agree with the reviewer and have adjusted the introduction based on the recommendations of the reviewer. Furthermore, we have adjusted the Discussion section of the manuscript by adding a short discussion about epistasis and additive effects affecting rhizomania resistance.

Reviewer Comment:
(2) The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
Author Response:
Unfortunately, the rights to the germplasm used in this trial are held by KWS Saat SE & Co. KGaA. We are therefore not in the position to publish this information. However, we have added a data availability statement to the manuscript stating that this information can be shared upon reasonable request.

Reviewer Comment:
(3) For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Author Response:
For the analysis, we have focused on the transformed data that were produced by transforming and averaging the ELISA measurements at all three time points. At the beginning of the results section, however, we have briefly described the OD measurements to show the range of the resulting OD values. Nevertheless, we agree with the reviewer that it is not clear why we have described the range of the OD values measured after 90 minutes and not after 60 and 120 minutes. Thus, we have added the range of the ELISA measurements after 60 and 120 minutes in the manuscript.

Reviewer Comment:
(4) Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
Author Response:
We appreciate the reviewer's criticism and agree that the current version of the manuscript lacked detailed information about the SNPs. Additionally, the reviewer correctly pointed out that, prior to MAF filtering, we are actually considering SNVs, not SNPs. However, we would like to keep referring to the SNVs as SNPs to improve readability of the manuscript since the data were collected using a SNP chip.

Reviewer Comment:
(5) The programs on Github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
Author Response:
We acknowledge the reviewer’s valuable feedback regarding the accessibility of the data from the trial on GitHub. We agree with the criticism and have significantly improved the documentation as requested. This should ensure that the data are now easily accessible and usable.

Reviewer Comment:
(6) In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
Author Response:
This was indeed a typo and we have corrected the corresponding part of the manuscript.

Reviewer Comment:
(7) It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
Author Response:
We have added genotype names for each individual in the data set on GitHub. Furthermore, we have given a special name for the genotype that was susceptible at Rz2 (``Control_susceptibleRz2'').

Reviewer Comment:
(8) For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
Author Response:
We thank the reviewer for this very attentive comment and have adjusted the corresponding part of the manuscript.

Reviewer Comment:
(9) Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
Author Response:
Following the suggestion, we conducted an analysis to assess the overlap of the selected SNPs. Our findings revealed that four SNPs were consistently identified through this approach. Subsequently, we have integrated this information into the manuscript, highlighting that these four detected SNPs account for a significant portion of the total variance in the phenotypic data.

Reviewer Comment:
(10) The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Author Response:
Thanks to the advice of the reviewer to analyse the overlap of selected SNPs, we discovered four SNPs that carry information about rhizomania resistance. In consultation with KWS Saat SE & Co. KGaA, we were allowed to publish the chromosomes on which these four SNPs are located. We show that two of the identified SNPs are not located on chromosome 3 but on chromosomes 2 and 5. We have included this new information in the manuscript which shows the importance of including SNPs from various chromosomes when examining SNP interactions.

Reviewer Comment:
(11) The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.
Author Response:
We appreciate the reviewer's feedback and acknowledge that the manuscript's writing style required enhancement. In response to the reviewer's criticism, we have refined the writing style of the manuscript to reduce redundancy in both the discussion and conclusion sections.
Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
Author Response:
We agree with the reviewer and have adjusted the introduction based on the recommendations of the reviewer. Furthermore, we have adjusted the Discussion section of the manuscript by adding a short discussion about epistasis and additive effects affecting rhizomania resistance.

Reviewer Comment:
(2) The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
Author Response:
Unfortunately, the rights to the germplasm used in this trial are held by KWS Saat SE & Co. KGaA. We are therefore not in the position to publish this information. However, we have added a data availability statement to the manuscript stating that this information can be shared upon reasonable request.

Reviewer Comment:
(3) For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Author Response:
For the analysis, we have focused on the transformed data that were produced by transforming and averaging the ELISA measurements at all three time points. At the beginning of the results section, however, we have briefly described the OD measurements to show the range of the resulting OD values. Nevertheless, we agree with the reviewer that it is not clear why we have described the range of the OD values measured after 90 minutes and not after 60 and 120 minutes. Thus, we have added the range of the ELISA measurements after 60 and 120 minutes in the manuscript.

Reviewer Comment:
(4) Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
Author Response:
We appreciate the reviewer's criticism and agree that the current version of the manuscript lacked detailed information about the SNPs. Additionally, the reviewer correctly pointed out that, prior to MAF filtering, we are actually considering SNVs, not SNPs. However, we would like to keep referring to the SNVs as SNPs to improve readability of the manuscript since the data were collected using a SNP chip.

Reviewer Comment:
(5) The programs on Github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
Author Response:
We acknowledge the reviewer’s valuable feedback regarding the accessibility of the data from the trial on GitHub. We agree with the criticism and have significantly improved the documentation as requested. This should ensure that the data are now easily accessible and usable.

Reviewer Comment:
(6) In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
Author Response:
This was indeed a typo and we have corrected the corresponding part of the manuscript.

Reviewer Comment:
(7) It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
Author Response:
We have added genotype names for each individual in the data set on GitHub. Furthermore, we have given a special name for the genotype that was susceptible at Rz2 (``Control_susceptibleRz2'').

Reviewer Comment:
(8) For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
Author Response:
We thank the reviewer for this very attentive comment and have adjusted the corresponding part of the manuscript.

Reviewer Comment:
(9) Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
Author Response:
Following the suggestion, we conducted an analysis to assess the overlap of the selected SNPs. Our findings revealed that four SNPs were consistently identified through this approach. Subsequently, we have integrated this information into the manuscript, highlighting that these four detected SNPs account for a significant portion of the total variance in the phenotypic data.

Reviewer Comment:
(10) The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Author Response:
Thanks to the advice of the reviewer to analyse the overlap of selected SNPs, we discovered four SNPs that carry information about rhizomania resistance. In consultation with KWS Saat SE & Co. KGaA, we were allowed to publish the chromosomes on which these four SNPs are located. We show that two of the identified SNPs are not located on chromosome 3 but on chromosomes 2 and 5. We have included this new information in the manuscript which shows the importance of including SNPs from various chromosomes when examining SNP interactions.

Reviewer Comment:
(11) The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.
Author Response:
We appreciate the reviewer's feedback and acknowledge that the manuscript's writing style required enhancement. In response to the reviewer's criticism, we have refined the writing style of the manuscript to reduce redundancy in both the discussion and conclusion sections.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 12 Sep 2023

Muhammad Massub Tehseen, Department of Plant Sciences, North Dakota State University, Fargo, North Dakota, USA

Not Approved

https://doi.org/10.5256/f1000research.143945.r201121

This paper aimed at comparing several four methods to investigate genomic prediction models to predict rhizomnia resistance in sugar beet. The topic is of general interest and the findings could be used in sugar beet breeding programs targeting rhizomnia resistance. However, there were certain limitations in the manuscript like insufficient description of Materials and methods, phenoytpic data not reliable, lacking novelty. The manuscript needs to be substantially revised to be able to be indexed.

First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by a cross and the progenies were advanced for two generations. It is very unclear as for what is happening, whether the 156 initial were used or the progenies derived from the cross? Why the crosses were made? The choice of parents and the reason or basis of selection? The authors assume the presence/absence of resistance which is not backed up by the variance in the phenotypic data generated. There should be detail description of the panel used, the experimental design, replications and phenotypic data generation.

The genomic prediction (GP) for any trait relies heavily on the traits heritability values, here the authors have claimed the maximum GP estimates of .030 which is fairly below moderate however it is hard to conclude its reliability without judging the quality and heritability values of the traits under study. Therefore, authors’ are suggested to estimate heritability before reporting any conclusions.

The analysis was conducted without including SNP in LD with the two resistance genes which seems to be strange and requires clarification from authors as why it was done? If the presence of highly associated SNPs would skew the prediction results then they should be mentioned and in fact presented side by side for comparison. Furthermore, to avoid the prediction ability influence by the low number of cross-validation i.e. 5-fold in the current study, each method should have run at least 100 CVs. If not 50 instead of just 10. The 10 times iteration generally just gives a rough idea of the prediction accuracy for more reliable estimates there should be at least 50 iterations.

As for the revision of the manuscript, the authors should avoid the lots of repetition and use of assumptions in the text. In many instances the assumed statements could be verified easily. The authors are requested to re-submit the revised manuscript to be considered for indexing.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Sugarbeet genetics, genomics and breeding.

CITE

Report a concern

Author Response 28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

28 Aug 2024

Author Response

Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by ... Continue reading Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by a cross and the progenies were advanced for two generations. It is very unclear as for what is happening, whether the 156 initial were used or the progenies derived from the cross? Why the crosses were made? The choice of parents and the reason or basis of selection? The authors assume the presence/absence of resistance which is not backed up by the variance in the phenotypic data generated. There should be detail description of the panel used, the experimental design, replications and phenotypic data generation.

Author Response:
We agree with the reviewer that the manuscript did not provide sufficient detail on how the sugar beet population in this trial was created. We have revised the corresponding paragraph to improve the clarity of the study.

Reviewer Comments:
(2) The genomic prediction (GP) for any trait relies heavily on the traits heritability values, here the authors have claimed the maximum GP estimates of .030 which is fairly below moderate however it is hard to conclude its reliability without judging the quality and heritability values of the traits under study. Therefore, authors’ are suggested to estimate heritability before reporting any conclusions.

Author Response:
It is important to clarify that our analysis focuses on the coefficient of determination (R²) rather than the correlation coefficient (r). R² is generally lower than r and represents the proportion of the variance explained by the model. In this context, the GP estimate of 0.30 suggests that a significant portion of the trait's variance can be explained by genomic information, demonstrating the potential of genomic prediction for this particular trait.

We agree that heritability estimates are crucial for assessing the reliability of GP and acknowledge the need to consider the quality and heritability values of the traits under study. Therefore, we concur with the reviewer's recommendation to include heritability estimates in future studies which would provide a more comprehensive understanding of the trait's predictability. In the current manuscript, our primary objective was to demonstrate the feasibility of genomic prediction for this trait, even with lower GP estimates. We believe that our results demonstrate potential in this area and we look forward to refining our analysis by incorporating heritability estimates in future research to strengthen our conclusions.

Reviewer Comments:
(3) The analysis was conducted without including SNP in LD with the two resistance genes which seems to be strange and requires clarification from authors as why it was done? If the presence of highly associated SNPs would skew the prediction results then they should be mentioned and in fact presented side by side for comparison. Furthermore, to avoid the prediction ability influence by the low number of cross-validation i.e. 5-fold in the current study, each method should have run at least 100 CVs. If not 50 instead of just 10. The 10 times iteration generally just gives a rough idea of the prediction accuracy for more reliable estimates there should be at least 50 iterations.

Author Response:
As thoroughly explained in the manuscript, each individual in the population is resistant at Rz1, with only one individual being susceptible at Rz2. The SNPs in high LD with the known resistance genes were not removed to skew prediction results. Instead, SNPs in high LD with Rz1 provide no variance and, thus, carry no useful information. The same applies to SNPs in high LD with Rz2, as they are identical for all but one individual in the population. Therefore, these SNPs were excluded in the minor allele frequency filtering step (MAF smaller than or equal to 0.05) which is standard practice to ensure minimum genetic variance in both the test and training data sets.

Regarding the second part of the criticism, the methods we used are computationally intensive, making it impractical to repeat the analysis 100 times as suggested. We employed a ten-fold repetition, consistent with similar research methodologies. For instance, Azodi et al. (2019) utilised this number of repetitions in their study on benchmarking parametric and machine learning models for genomic prediction of complex traits. As stated in the manuscript, our R script and data are publicly available and we encourage the reviewer or any interested party to replicate the study with a higher number of repetitions if desired.

Reviewer Comments:
(4) As for the revision of the manuscript, the authors should avoid the lots of repetition and use of assumptions in the text. In many instances the assumed statements could be verified easily. The authors are requested to re-submit the revised manuscript to be considered for indexing.

Author Response:
We appreciate the reviewer's criticism and agree that the manuscript's writing style required enhancement. We have revised the manuscript to improve the writing style, addressing the reviewer's concerns by reducing repetitions and clarifying assumptions.
Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by a cross and the progenies were advanced for two generations. It is very unclear as for what is happening, whether the 156 initial were used or the progenies derived from the cross? Why the crosses were made? The choice of parents and the reason or basis of selection? The authors assume the presence/absence of resistance which is not backed up by the variance in the phenotypic data generated. There should be detail description of the panel used, the experimental design, replications and phenotypic data generation.

Author Response:
We agree with the reviewer that the manuscript did not provide sufficient detail on how the sugar beet population in this trial was created. We have revised the corresponding paragraph to improve the clarity of the study.

Reviewer Comments:
(2) The genomic prediction (GP) for any trait relies heavily on the traits heritability values, here the authors have claimed the maximum GP estimates of .030 which is fairly below moderate however it is hard to conclude its reliability without judging the quality and heritability values of the traits under study. Therefore, authors’ are suggested to estimate heritability before reporting any conclusions.

Author Response:
It is important to clarify that our analysis focuses on the coefficient of determination (R²) rather than the correlation coefficient (r). R² is generally lower than r and represents the proportion of the variance explained by the model. In this context, the GP estimate of 0.30 suggests that a significant portion of the trait's variance can be explained by genomic information, demonstrating the potential of genomic prediction for this particular trait.

We agree that heritability estimates are crucial for assessing the reliability of GP and acknowledge the need to consider the quality and heritability values of the traits under study. Therefore, we concur with the reviewer's recommendation to include heritability estimates in future studies which would provide a more comprehensive understanding of the trait's predictability. In the current manuscript, our primary objective was to demonstrate the feasibility of genomic prediction for this trait, even with lower GP estimates. We believe that our results demonstrate potential in this area and we look forward to refining our analysis by incorporating heritability estimates in future research to strengthen our conclusions.

Reviewer Comments:
(3) The analysis was conducted without including SNP in LD with the two resistance genes which seems to be strange and requires clarification from authors as why it was done? If the presence of highly associated SNPs would skew the prediction results then they should be mentioned and in fact presented side by side for comparison. Furthermore, to avoid the prediction ability influence by the low number of cross-validation i.e. 5-fold in the current study, each method should have run at least 100 CVs. If not 50 instead of just 10. The 10 times iteration generally just gives a rough idea of the prediction accuracy for more reliable estimates there should be at least 50 iterations.

Author Response:
As thoroughly explained in the manuscript, each individual in the population is resistant at Rz1, with only one individual being susceptible at Rz2. The SNPs in high LD with the known resistance genes were not removed to skew prediction results. Instead, SNPs in high LD with Rz1 provide no variance and, thus, carry no useful information. The same applies to SNPs in high LD with Rz2, as they are identical for all but one individual in the population. Therefore, these SNPs were excluded in the minor allele frequency filtering step (MAF smaller than or equal to 0.05) which is standard practice to ensure minimum genetic variance in both the test and training data sets.

Regarding the second part of the criticism, the methods we used are computationally intensive, making it impractical to repeat the analysis 100 times as suggested. We employed a ten-fold repetition, consistent with similar research methodologies. For instance, Azodi et al. (2019) utilised this number of repetitions in their study on benchmarking parametric and machine learning models for genomic prediction of complex traits. As stated in the manuscript, our R script and data are publicly available and we encourage the reviewer or any interested party to replicate the study with a higher number of repetitions if desired.

Reviewer Comments:
(4) As for the revision of the manuscript, the authors should avoid the lots of repetition and use of assumptions in the text. In many instances the assumed statements could be verified easily. The authors are requested to re-submit the revised manuscript to be considered for indexing.

Author Response:
We appreciate the reviewer's criticism and agree that the manuscript's writing style required enhancement. We have revised the manuscript to improve the writing style, addressing the reviewer's concerns by reducing repetitions and clarifying assumptions.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

28 Aug 2024

Author Response

Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by ... Continue reading Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by a cross and the progenies were advanced for two generations. It is very unclear as for what is happening, whether the 156 initial were used or the progenies derived from the cross? Why the crosses were made? The choice of parents and the reason or basis of selection? The authors assume the presence/absence of resistance which is not backed up by the variance in the phenotypic data generated. There should be detail description of the panel used, the experimental design, replications and phenotypic data generation.

Author Response:
We agree with the reviewer that the manuscript did not provide sufficient detail on how the sugar beet population in this trial was created. We have revised the corresponding paragraph to improve the clarity of the study.

Reviewer Comments:
(2) The genomic prediction (GP) for any trait relies heavily on the traits heritability values, here the authors have claimed the maximum GP estimates of .030 which is fairly below moderate however it is hard to conclude its reliability without judging the quality and heritability values of the traits under study. Therefore, authors’ are suggested to estimate heritability before reporting any conclusions.

Author Response:
It is important to clarify that our analysis focuses on the coefficient of determination (R²) rather than the correlation coefficient (r). R² is generally lower than r and represents the proportion of the variance explained by the model. In this context, the GP estimate of 0.30 suggests that a significant portion of the trait's variance can be explained by genomic information, demonstrating the potential of genomic prediction for this particular trait.

We agree that heritability estimates are crucial for assessing the reliability of GP and acknowledge the need to consider the quality and heritability values of the traits under study. Therefore, we concur with the reviewer's recommendation to include heritability estimates in future studies which would provide a more comprehensive understanding of the trait's predictability. In the current manuscript, our primary objective was to demonstrate the feasibility of genomic prediction for this trait, even with lower GP estimates. We believe that our results demonstrate potential in this area and we look forward to refining our analysis by incorporating heritability estimates in future research to strengthen our conclusions.

Reviewer Comments:
(3) The analysis was conducted without including SNP in LD with the two resistance genes which seems to be strange and requires clarification from authors as why it was done? If the presence of highly associated SNPs would skew the prediction results then they should be mentioned and in fact presented side by side for comparison. Furthermore, to avoid the prediction ability influence by the low number of cross-validation i.e. 5-fold in the current study, each method should have run at least 100 CVs. If not 50 instead of just 10. The 10 times iteration generally just gives a rough idea of the prediction accuracy for more reliable estimates there should be at least 50 iterations.

Author Response:
As thoroughly explained in the manuscript, each individual in the population is resistant at Rz1, with only one individual being susceptible at Rz2. The SNPs in high LD with the known resistance genes were not removed to skew prediction results. Instead, SNPs in high LD with Rz1 provide no variance and, thus, carry no useful information. The same applies to SNPs in high LD with Rz2, as they are identical for all but one individual in the population. Therefore, these SNPs were excluded in the minor allele frequency filtering step (MAF smaller than or equal to 0.05) which is standard practice to ensure minimum genetic variance in both the test and training data sets.

Regarding the second part of the criticism, the methods we used are computationally intensive, making it impractical to repeat the analysis 100 times as suggested. We employed a ten-fold repetition, consistent with similar research methodologies. For instance, Azodi et al. (2019) utilised this number of repetitions in their study on benchmarking parametric and machine learning models for genomic prediction of complex traits. As stated in the manuscript, our R script and data are publicly available and we encourage the reviewer or any interested party to replicate the study with a higher number of repetitions if desired.

Reviewer Comments:
(4) As for the revision of the manuscript, the authors should avoid the lots of repetition and use of assumptions in the text. In many instances the assumed statements could be verified easily. The authors are requested to re-submit the revised manuscript to be considered for indexing.

Author Response:
We appreciate the reviewer's criticism and agree that the manuscript's writing style required enhancement. We have revised the manuscript to improve the writing style, addressing the reviewer's concerns by reducing repetitions and clarifying assumptions.
Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by a cross and the progenies were advanced for two generations. It is very unclear as for what is happening, whether the 156 initial were used or the progenies derived from the cross? Why the crosses were made? The choice of parents and the reason or basis of selection? The authors assume the presence/absence of resistance which is not backed up by the variance in the phenotypic data generated. There should be detail description of the panel used, the experimental design, replications and phenotypic data generation.

Author Response:
We agree with the reviewer that the manuscript did not provide sufficient detail on how the sugar beet population in this trial was created. We have revised the corresponding paragraph to improve the clarity of the study.

Reviewer Comments:
(2) The genomic prediction (GP) for any trait relies heavily on the traits heritability values, here the authors have claimed the maximum GP estimates of .030 which is fairly below moderate however it is hard to conclude its reliability without judging the quality and heritability values of the traits under study. Therefore, authors’ are suggested to estimate heritability before reporting any conclusions.

Author Response:
It is important to clarify that our analysis focuses on the coefficient of determination (R²) rather than the correlation coefficient (r). R² is generally lower than r and represents the proportion of the variance explained by the model. In this context, the GP estimate of 0.30 suggests that a significant portion of the trait's variance can be explained by genomic information, demonstrating the potential of genomic prediction for this particular trait.

We agree that heritability estimates are crucial for assessing the reliability of GP and acknowledge the need to consider the quality and heritability values of the traits under study. Therefore, we concur with the reviewer's recommendation to include heritability estimates in future studies which would provide a more comprehensive understanding of the trait's predictability. In the current manuscript, our primary objective was to demonstrate the feasibility of genomic prediction for this trait, even with lower GP estimates. We believe that our results demonstrate potential in this area and we look forward to refining our analysis by incorporating heritability estimates in future research to strengthen our conclusions.

Reviewer Comments:
(3) The analysis was conducted without including SNP in LD with the two resistance genes which seems to be strange and requires clarification from authors as why it was done? If the presence of highly associated SNPs would skew the prediction results then they should be mentioned and in fact presented side by side for comparison. Furthermore, to avoid the prediction ability influence by the low number of cross-validation i.e. 5-fold in the current study, each method should have run at least 100 CVs. If not 50 instead of just 10. The 10 times iteration generally just gives a rough idea of the prediction accuracy for more reliable estimates there should be at least 50 iterations.

Author Response:
As thoroughly explained in the manuscript, each individual in the population is resistant at Rz1, with only one individual being susceptible at Rz2. The SNPs in high LD with the known resistance genes were not removed to skew prediction results. Instead, SNPs in high LD with Rz1 provide no variance and, thus, carry no useful information. The same applies to SNPs in high LD with Rz2, as they are identical for all but one individual in the population. Therefore, these SNPs were excluded in the minor allele frequency filtering step (MAF smaller than or equal to 0.05) which is standard practice to ensure minimum genetic variance in both the test and training data sets.

Regarding the second part of the criticism, the methods we used are computationally intensive, making it impractical to repeat the analysis 100 times as suggested. We employed a ten-fold repetition, consistent with similar research methodologies. For instance, Azodi et al. (2019) utilised this number of repetitions in their study on benchmarking parametric and machine learning models for genomic prediction of complex traits. As stated in the manuscript, our R script and data are publicly available and we encourage the reviewer or any interested party to replicate the study with a higher number of repetitions if desired.

Reviewer Comments:
(4) As for the revision of the manuscript, the authors should avoid the lots of repetition and use of assumptions in the text. In many instances the assumed statements could be verified easily. The authors are requested to re-submit the revised manuscript to be considered for indexing.

Author Response:
We appreciate the reviewer's criticism and agree that the manuscript's writing style required enhancement. We have revised the manuscript to improve the writing style, addressing the reviewer's concerns by reducing repetitions and clarifying assumptions.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 28 Jul 2023

J Mitchell McGrath, USDA-ARS Sugarbeet and Bean Research Unit, Michigan State University, East Lansing, Michigan, USA

Not Approved

https://doi.org/10.5256/f1000research.143945.r181537

First review of draft of "Improving genomic prediction of rhizomania resistance in sugar beet (Beta vulgaris L.) by implementing epistatic effects and feature selection." by Lange et al. (doi.org/10.12688/f1000research.131134.1) for potential indexing.

This manuscript details computational investigations using genomic prediction methods to evaluate rhizomania resistance in sugar beet. The topic is very important and results would be useful for sugar beet breeders, and other scientists interested in genomic prediction for their traits of interest. The approach taken is valid, and the authors are highly regarded with good facilities and means to accomplish their task. The authors appear to have generated some evidence suggesting additional factors beyond the traditional single gene rhizomania resistances may be available for breeding enhancement for rhizomania resistance, however, the manuscript needs revision to make this clearer and marginally useful.

It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used were 'assumed' to carry the relevant genes Rz1 and Rz2 (in all but one of 156 entries) (gene symbols need to be italicized in publication). It is entirely unclear what material was used (presumably material initiating from KWS), with one statement suggesting 156 lines and, conversely, a following statement that two lines were crossed and selfed for two generations. Which of these are the population(s) for which the analyses were done? And if both, it needs to be made clearer in the text, as well as for what question each of the populations was used. A list of germplasm used should be included.

Analyses proceeded without using SNPs for the two named resistance genes, and I think this is a flaw in the logic of the paper. Evidence for the assumption that the germplasm is resistant is essential. Assuming the author's assumption is valid, the logic for excluding SNPs for Rz1 and Rz2 should be presented. I suspect there may have been a concern that the known genes with major effect may have overwhelmed the signal from discovered modifiers (the point of the manuscript), however this needs to be demonstrated. If this is the case, what are the implications for the 'strength' or 'effectiveness' of the discovered modifiers? Since the manuscript deals strictly with in silico investigations, it seems a relatively small matter to test the effect of named resistance genes on the results, and then exclude for cause if that is indeed the case.

The author's writing suggests many assumptions were used in their analyses. It is difficult to interpret what is indeed a true assumption from a postulate they wish to have tested, so purging the manuscript for words relating to 'assume' would create better credibility for the work, unless it is absolutely essential (and even then with clear implication for their results if the assumption does not hold). (For many assumptions presented, relatively simple procedures can validate them, which may have been done in the course of the work.) Excluding SNPs with a major allele frequency of >0.95 seems arbitrary as well, although as above, it is difficult to ascertain the author's intent given the questions of the population(s) evaluated. So, in that respect, the manuscript can not be properly vetted yet.

As suggestions for revision, clarity of writing for an audience is essential. Right now, this seems to be a draft that organizes the authors' thoughts into a manuscript format. Jargon should be avoided. Assumptions should be justified. Where available, actual numbers should be presented (rather than qualitative statements such as 'many', 'the remaining', etc.) to allow the reader to properly account for the process obtaining results. Concepts used should be defined (e.g. 'variable importance', 'technical limit', etc.). I would also like to see what genomic regions the author's have discovered and how the different methods/ algorithms differed with respect to the types of genes and elements discovered. Specifically, one needs evidence that this approach is likely to be successful. Or, if this is a manuscript describing negative results, that should be stated as well.

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Genetics, genomics, and germplasm enhancement of sugar beet

CITE

Report a concern

Author Response 28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

28 Aug 2024

Author Response

Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used ... Continue reading Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used were 'assumed' to carry the relevant genes Rz1 and Rz2 (in all but one of 156 entries) (gene symbols need to be italicized in publication). It is entirely unclear what material was used (presumably material initiating from KWS), with one statement suggesting 156 lines and, conversely, a following statement that two lines were crossed and selfed for two generations. Which of these are the population(s) for which the analyses were done? And if both, it needs to be made clearer in the text, as well as for what question each of the populations was used. A list of germplasm used should be included.

Author Response:
After revising the addressed paragraph, we agree with the reviewer's assessment. The paragraph describing the experimental design and, notably, the composition of the analysed population was overly complex and did not clearly articulate how the population was established. We have revised the paragraph to provide a clearer explanation of the population's creation and genotyping process.

Additionally, the reviewer raised concerns regarding the lack of naming for the initial two sugar beet lines used to create this population. We acknowledge that the rights to the germplasm utilised in this trial are held by KWS Saat SE & Co. KGaA, and as such, we are unable to disclose this information. However, in response to the reviewer's criticism, we have included a data availability statement in the manuscript and italicised the gene names.

Reviewer Comment:
(2) Analyses proceeded without using SNPs for the two named resistance genes, and I think this is a flaw in the logic of the paper. Evidence for the assumption that the germplasm is resistant is essential. Assuming the author's assumption is valid, the logic for excluding SNPs for Rz1 and Rz2 should be presented. I suspect there may have been a concern that the known genes with major effect may have overwhelmed the signal from discovered modifiers (the point of the manuscript), however this needs to be demonstrated. If this is the case, what are the implications for the 'strength' or 'effectiveness' of the discovered modifiers? Since the manuscript deals strictly with in silico investigations, it seems a relatively small matter to test the effect of named resistance genes on the results, and then exclude for cause if that is indeed the case.

Author Response:
We appreciate the reviewer's point regarding the importance of providing evidence for the assumption of germplasm resistance. Indeed, we have conducted an analysis of the resistance of the population at Rz1 and Rz2 using SNP markers. However, it is crucial to note that the SNPs in high linkage disequilibrium (LD) with Rz1 and Rz2 exhibit minimal genetic variance because all plants in the population are resistant at the two known resistance genes. Consequently, these SNPs do not contribute any meaningful information and are unsuitable for genomic prediction. Consequently, these SNPs were removed due to minor allele frequency filtering (MAF smaller than or equal to 0.05). We recognise that the omission of this information about the removal of SNPs in high LD with the resistance genes may has caused confusion, and we have thoroughly adjusted the Materials and Methods section of the manuscript to clarify this aspect.

Reviewer Comment:
(3) The author's writing suggests many assumptions were used in their analyses. It is difficult to interpret what is indeed a true assumption from a postulate they wish to have tested, so purging the manuscript for words relating to 'assume' would create better credibility for the work, unless it is absolutely essential (and even then with clear implication for their results if the assumption does not hold). (For many assumptions presented, relatively simple procedures can validate them, which may have been done in the course of the work.) Excluding SNPs with a major allele frequency of >0.95 seems arbitrary as well, although as above, it is difficult to ascertain the author's intent given the questions of the population(s) evaluated. So, in that respect, the manuscript can not be properly vetted yet.

Author Response:
We acknowledge the reviewer's feedback and have revised the manuscript accordingly. We acknowledge that the term "to assume" was overused, particularly when describing the "assumption" that the plants are resistant at Rz1 and Rz2. As detailed in the manuscript, the plants were analysed using SNP markers. All genotypes were homozygous for the resistance gene at SNPs in high LD with Rz1, and 155 out of 156 genotypes were homozygous for the resistance gene at SNPs in high LD with Rz2. However, we use the term "to assume" because LD does not provide absolute certainty that an individual carries the specified gene when the corresponding SNP marker shows a particular allele. Nonetheless, the reviewer's point is well taken, and we have adjusted the relevant sections to enhance the manuscript's readability.

Furthermore, the reviewer criticised the removal of SNPs with a major allele frequency of 0.95 or higher from the data set. This practice is common to ensure that each SNP contributes sufficient genetic variance in both the training and test populations. Therefore, we do not intend to alter this aspect of the method or the corresponding section of the manuscript.

Reviewer Comment:
(4) As suggestions for revision, clarity of writing for an audience is essential. Right now, this seems to be a draft that organizes the authors' thoughts into a manuscript format. Jargon should be avoided. Assumptions should be justified. Where available, actual numbers should be presented (rather than qualitative statements such as 'many', 'the remaining', etc.) to allow the reader to properly account for the process obtaining results. Concepts used should be defined (e.g. 'variable importance', 'technical limit', etc.). I would also like to see what genomic regions the author's have discovered and how the different methods/ algorithms differed with respect to the types of genes and elements discovered. Specifically, one needs evidence that this approach is likely to be successful. Or, if this is a manuscript describing negative results, that should be stated as well.

Author Response:
We appreciate the reviewer's feedback and agree that the writing style of the manuscript required improvement. We have revised the manuscript accordingly. Definitions of technical terms, such as variable importance and the technical limit of the machine, have been added for clarity. Additionally, we have included more information on the overlap in methods regarding the detection of important SNPs. In response to the reviewer's criticism, KWS Saat SE & Co. KGaA agreed to publish the chromosomes on which SNPs are located that were detected using our method. We have also added a data availability statement to the manuscript stating that the exact position on the chromosome as well as the genomic positions of the other SNPs in this data set are available upon reasonable request.
Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used were 'assumed' to carry the relevant genes Rz1 and Rz2 (in all but one of 156 entries) (gene symbols need to be italicized in publication). It is entirely unclear what material was used (presumably material initiating from KWS), with one statement suggesting 156 lines and, conversely, a following statement that two lines were crossed and selfed for two generations. Which of these are the population(s) for which the analyses were done? And if both, it needs to be made clearer in the text, as well as for what question each of the populations was used. A list of germplasm used should be included.

Author Response:
After revising the addressed paragraph, we agree with the reviewer's assessment. The paragraph describing the experimental design and, notably, the composition of the analysed population was overly complex and did not clearly articulate how the population was established. We have revised the paragraph to provide a clearer explanation of the population's creation and genotyping process.

Additionally, the reviewer raised concerns regarding the lack of naming for the initial two sugar beet lines used to create this population. We acknowledge that the rights to the germplasm utilised in this trial are held by KWS Saat SE & Co. KGaA, and as such, we are unable to disclose this information. However, in response to the reviewer's criticism, we have included a data availability statement in the manuscript and italicised the gene names.

Reviewer Comment:
(2) Analyses proceeded without using SNPs for the two named resistance genes, and I think this is a flaw in the logic of the paper. Evidence for the assumption that the germplasm is resistant is essential. Assuming the author's assumption is valid, the logic for excluding SNPs for Rz1 and Rz2 should be presented. I suspect there may have been a concern that the known genes with major effect may have overwhelmed the signal from discovered modifiers (the point of the manuscript), however this needs to be demonstrated. If this is the case, what are the implications for the 'strength' or 'effectiveness' of the discovered modifiers? Since the manuscript deals strictly with in silico investigations, it seems a relatively small matter to test the effect of named resistance genes on the results, and then exclude for cause if that is indeed the case.

Author Response:
We appreciate the reviewer's point regarding the importance of providing evidence for the assumption of germplasm resistance. Indeed, we have conducted an analysis of the resistance of the population at Rz1 and Rz2 using SNP markers. However, it is crucial to note that the SNPs in high linkage disequilibrium (LD) with Rz1 and Rz2 exhibit minimal genetic variance because all plants in the population are resistant at the two known resistance genes. Consequently, these SNPs do not contribute any meaningful information and are unsuitable for genomic prediction. Consequently, these SNPs were removed due to minor allele frequency filtering (MAF smaller than or equal to 0.05). We recognise that the omission of this information about the removal of SNPs in high LD with the resistance genes may has caused confusion, and we have thoroughly adjusted the Materials and Methods section of the manuscript to clarify this aspect.

Reviewer Comment:
(3) The author's writing suggests many assumptions were used in their analyses. It is difficult to interpret what is indeed a true assumption from a postulate they wish to have tested, so purging the manuscript for words relating to 'assume' would create better credibility for the work, unless it is absolutely essential (and even then with clear implication for their results if the assumption does not hold). (For many assumptions presented, relatively simple procedures can validate them, which may have been done in the course of the work.) Excluding SNPs with a major allele frequency of >0.95 seems arbitrary as well, although as above, it is difficult to ascertain the author's intent given the questions of the population(s) evaluated. So, in that respect, the manuscript can not be properly vetted yet.

Author Response:
We acknowledge the reviewer's feedback and have revised the manuscript accordingly. We acknowledge that the term "to assume" was overused, particularly when describing the "assumption" that the plants are resistant at Rz1 and Rz2. As detailed in the manuscript, the plants were analysed using SNP markers. All genotypes were homozygous for the resistance gene at SNPs in high LD with Rz1, and 155 out of 156 genotypes were homozygous for the resistance gene at SNPs in high LD with Rz2. However, we use the term "to assume" because LD does not provide absolute certainty that an individual carries the specified gene when the corresponding SNP marker shows a particular allele. Nonetheless, the reviewer's point is well taken, and we have adjusted the relevant sections to enhance the manuscript's readability.

Furthermore, the reviewer criticised the removal of SNPs with a major allele frequency of 0.95 or higher from the data set. This practice is common to ensure that each SNP contributes sufficient genetic variance in both the training and test populations. Therefore, we do not intend to alter this aspect of the method or the corresponding section of the manuscript.

Reviewer Comment:
(4) As suggestions for revision, clarity of writing for an audience is essential. Right now, this seems to be a draft that organizes the authors' thoughts into a manuscript format. Jargon should be avoided. Assumptions should be justified. Where available, actual numbers should be presented (rather than qualitative statements such as 'many', 'the remaining', etc.) to allow the reader to properly account for the process obtaining results. Concepts used should be defined (e.g. 'variable importance', 'technical limit', etc.). I would also like to see what genomic regions the author's have discovered and how the different methods/ algorithms differed with respect to the types of genes and elements discovered. Specifically, one needs evidence that this approach is likely to be successful. Or, if this is a manuscript describing negative results, that should be stated as well.

Author Response:
We appreciate the reviewer's feedback and agree that the writing style of the manuscript required improvement. We have revised the manuscript accordingly. Definitions of technical terms, such as variable importance and the technical limit of the machine, have been added for clarity. Additionally, we have included more information on the overlap in methods regarding the detection of important SNPs. In response to the reviewer's criticism, KWS Saat SE & Co. KGaA agreed to publish the chromosomes on which SNPs are located that were detected using our method. We have also added a data availability statement to the manuscript stating that the exact position on the chromosome as well as the genomic positions of the other SNPs in this data set are available upon reasonable request.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

28 Aug 2024

Author Response

Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used ... Continue reading Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used were 'assumed' to carry the relevant genes Rz1 and Rz2 (in all but one of 156 entries) (gene symbols need to be italicized in publication). It is entirely unclear what material was used (presumably material initiating from KWS), with one statement suggesting 156 lines and, conversely, a following statement that two lines were crossed and selfed for two generations. Which of these are the population(s) for which the analyses were done? And if both, it needs to be made clearer in the text, as well as for what question each of the populations was used. A list of germplasm used should be included.

Author Response:
After revising the addressed paragraph, we agree with the reviewer's assessment. The paragraph describing the experimental design and, notably, the composition of the analysed population was overly complex and did not clearly articulate how the population was established. We have revised the paragraph to provide a clearer explanation of the population's creation and genotyping process.

Additionally, the reviewer raised concerns regarding the lack of naming for the initial two sugar beet lines used to create this population. We acknowledge that the rights to the germplasm utilised in this trial are held by KWS Saat SE & Co. KGaA, and as such, we are unable to disclose this information. However, in response to the reviewer's criticism, we have included a data availability statement in the manuscript and italicised the gene names.

Reviewer Comment:
(2) Analyses proceeded without using SNPs for the two named resistance genes, and I think this is a flaw in the logic of the paper. Evidence for the assumption that the germplasm is resistant is essential. Assuming the author's assumption is valid, the logic for excluding SNPs for Rz1 and Rz2 should be presented. I suspect there may have been a concern that the known genes with major effect may have overwhelmed the signal from discovered modifiers (the point of the manuscript), however this needs to be demonstrated. If this is the case, what are the implications for the 'strength' or 'effectiveness' of the discovered modifiers? Since the manuscript deals strictly with in silico investigations, it seems a relatively small matter to test the effect of named resistance genes on the results, and then exclude for cause if that is indeed the case.

Author Response:
We appreciate the reviewer's point regarding the importance of providing evidence for the assumption of germplasm resistance. Indeed, we have conducted an analysis of the resistance of the population at Rz1 and Rz2 using SNP markers. However, it is crucial to note that the SNPs in high linkage disequilibrium (LD) with Rz1 and Rz2 exhibit minimal genetic variance because all plants in the population are resistant at the two known resistance genes. Consequently, these SNPs do not contribute any meaningful information and are unsuitable for genomic prediction. Consequently, these SNPs were removed due to minor allele frequency filtering (MAF smaller than or equal to 0.05). We recognise that the omission of this information about the removal of SNPs in high LD with the resistance genes may has caused confusion, and we have thoroughly adjusted the Materials and Methods section of the manuscript to clarify this aspect.

Reviewer Comment:
(3) The author's writing suggests many assumptions were used in their analyses. It is difficult to interpret what is indeed a true assumption from a postulate they wish to have tested, so purging the manuscript for words relating to 'assume' would create better credibility for the work, unless it is absolutely essential (and even then with clear implication for their results if the assumption does not hold). (For many assumptions presented, relatively simple procedures can validate them, which may have been done in the course of the work.) Excluding SNPs with a major allele frequency of >0.95 seems arbitrary as well, although as above, it is difficult to ascertain the author's intent given the questions of the population(s) evaluated. So, in that respect, the manuscript can not be properly vetted yet.

Author Response:
We acknowledge the reviewer's feedback and have revised the manuscript accordingly. We acknowledge that the term "to assume" was overused, particularly when describing the "assumption" that the plants are resistant at Rz1 and Rz2. As detailed in the manuscript, the plants were analysed using SNP markers. All genotypes were homozygous for the resistance gene at SNPs in high LD with Rz1, and 155 out of 156 genotypes were homozygous for the resistance gene at SNPs in high LD with Rz2. However, we use the term "to assume" because LD does not provide absolute certainty that an individual carries the specified gene when the corresponding SNP marker shows a particular allele. Nonetheless, the reviewer's point is well taken, and we have adjusted the relevant sections to enhance the manuscript's readability.

Furthermore, the reviewer criticised the removal of SNPs with a major allele frequency of 0.95 or higher from the data set. This practice is common to ensure that each SNP contributes sufficient genetic variance in both the training and test populations. Therefore, we do not intend to alter this aspect of the method or the corresponding section of the manuscript.

Reviewer Comment:
(4) As suggestions for revision, clarity of writing for an audience is essential. Right now, this seems to be a draft that organizes the authors' thoughts into a manuscript format. Jargon should be avoided. Assumptions should be justified. Where available, actual numbers should be presented (rather than qualitative statements such as 'many', 'the remaining', etc.) to allow the reader to properly account for the process obtaining results. Concepts used should be defined (e.g. 'variable importance', 'technical limit', etc.). I would also like to see what genomic regions the author's have discovered and how the different methods/ algorithms differed with respect to the types of genes and elements discovered. Specifically, one needs evidence that this approach is likely to be successful. Or, if this is a manuscript describing negative results, that should be stated as well.

Author Response:
We appreciate the reviewer's feedback and agree that the writing style of the manuscript required improvement. We have revised the manuscript accordingly. Definitions of technical terms, such as variable importance and the technical limit of the machine, have been added for clarity. Additionally, we have included more information on the overlap in methods regarding the detection of important SNPs. In response to the reviewer's criticism, KWS Saat SE & Co. KGaA agreed to publish the chromosomes on which SNPs are located that were detected using our method. We have also added a data availability statement to the manuscript stating that the exact position on the chromosome as well as the genomic positions of the other SNPs in this data set are available upon reasonable request.
Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used were 'assumed' to carry the relevant genes Rz1 and Rz2 (in all but one of 156 entries) (gene symbols need to be italicized in publication). It is entirely unclear what material was used (presumably material initiating from KWS), with one statement suggesting 156 lines and, conversely, a following statement that two lines were crossed and selfed for two generations. Which of these are the population(s) for which the analyses were done? And if both, it needs to be made clearer in the text, as well as for what question each of the populations was used. A list of germplasm used should be included.

Author Response:
After revising the addressed paragraph, we agree with the reviewer's assessment. The paragraph describing the experimental design and, notably, the composition of the analysed population was overly complex and did not clearly articulate how the population was established. We have revised the paragraph to provide a clearer explanation of the population's creation and genotyping process.

Additionally, the reviewer raised concerns regarding the lack of naming for the initial two sugar beet lines used to create this population. We acknowledge that the rights to the germplasm utilised in this trial are held by KWS Saat SE & Co. KGaA, and as such, we are unable to disclose this information. However, in response to the reviewer's criticism, we have included a data availability statement in the manuscript and italicised the gene names.

Reviewer Comment:
(2) Analyses proceeded without using SNPs for the two named resistance genes, and I think this is a flaw in the logic of the paper. Evidence for the assumption that the germplasm is resistant is essential. Assuming the author's assumption is valid, the logic for excluding SNPs for Rz1 and Rz2 should be presented. I suspect there may have been a concern that the known genes with major effect may have overwhelmed the signal from discovered modifiers (the point of the manuscript), however this needs to be demonstrated. If this is the case, what are the implications for the 'strength' or 'effectiveness' of the discovered modifiers? Since the manuscript deals strictly with in silico investigations, it seems a relatively small matter to test the effect of named resistance genes on the results, and then exclude for cause if that is indeed the case.

Author Response:
We appreciate the reviewer's point regarding the importance of providing evidence for the assumption of germplasm resistance. Indeed, we have conducted an analysis of the resistance of the population at Rz1 and Rz2 using SNP markers. However, it is crucial to note that the SNPs in high linkage disequilibrium (LD) with Rz1 and Rz2 exhibit minimal genetic variance because all plants in the population are resistant at the two known resistance genes. Consequently, these SNPs do not contribute any meaningful information and are unsuitable for genomic prediction. Consequently, these SNPs were removed due to minor allele frequency filtering (MAF smaller than or equal to 0.05). We recognise that the omission of this information about the removal of SNPs in high LD with the resistance genes may has caused confusion, and we have thoroughly adjusted the Materials and Methods section of the manuscript to clarify this aspect.

Reviewer Comment:
(3) The author's writing suggests many assumptions were used in their analyses. It is difficult to interpret what is indeed a true assumption from a postulate they wish to have tested, so purging the manuscript for words relating to 'assume' would create better credibility for the work, unless it is absolutely essential (and even then with clear implication for their results if the assumption does not hold). (For many assumptions presented, relatively simple procedures can validate them, which may have been done in the course of the work.) Excluding SNPs with a major allele frequency of >0.95 seems arbitrary as well, although as above, it is difficult to ascertain the author's intent given the questions of the population(s) evaluated. So, in that respect, the manuscript can not be properly vetted yet.

Author Response:
We acknowledge the reviewer's feedback and have revised the manuscript accordingly. We acknowledge that the term "to assume" was overused, particularly when describing the "assumption" that the plants are resistant at Rz1 and Rz2. As detailed in the manuscript, the plants were analysed using SNP markers. All genotypes were homozygous for the resistance gene at SNPs in high LD with Rz1, and 155 out of 156 genotypes were homozygous for the resistance gene at SNPs in high LD with Rz2. However, we use the term "to assume" because LD does not provide absolute certainty that an individual carries the specified gene when the corresponding SNP marker shows a particular allele. Nonetheless, the reviewer's point is well taken, and we have adjusted the relevant sections to enhance the manuscript's readability.

Furthermore, the reviewer criticised the removal of SNPs with a major allele frequency of 0.95 or higher from the data set. This practice is common to ensure that each SNP contributes sufficient genetic variance in both the training and test populations. Therefore, we do not intend to alter this aspect of the method or the corresponding section of the manuscript.

Reviewer Comment:
(4) As suggestions for revision, clarity of writing for an audience is essential. Right now, this seems to be a draft that organizes the authors' thoughts into a manuscript format. Jargon should be avoided. Assumptions should be justified. Where available, actual numbers should be presented (rather than qualitative statements such as 'many', 'the remaining', etc.) to allow the reader to properly account for the process obtaining results. Concepts used should be defined (e.g. 'variable importance', 'technical limit', etc.). I would also like to see what genomic regions the author's have discovered and how the different methods/ algorithms differed with respect to the types of genes and elements discovered. Specifically, one needs evidence that this approach is likely to be successful. Or, if this is a manuscript describing negative results, that should be stated as well.

Author Response:
We appreciate the reviewer's feedback and agree that the writing style of the manuscript required improvement. We have revised the manuscript accordingly. Definitions of technical terms, such as variable importance and the technical limit of the machine, have been added for clarity. Additionally, we have included more information on the overlap in methods regarding the detection of important SNPs. In response to the reviewer's criticism, KWS Saat SE & Co. KGaA agreed to publish the chromosomes on which SNPs are located that were detected using our method. We have also added a data availability statement to the manuscript stating that the exact position on the chromosome as well as the genomic positions of the other SNPs in this data set are available upon reasonable request.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 14 Mar 2023

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2	3	4
Version 2 (revision) 28 Aug 24			read	read
Version 1 14 Mar 23	read	read	read

J Mitchell McGrath, Michigan State University, East Lansing, USA
Muhammad Massub Tehseen, North Dakota State University, Fargo, USA
Daniela Holtgräwe, Bielefeld University, Bielefeld, Germany
Chenggen Chu, USDA-ARS, North Dakota, USA

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

1 Views

27 Nov 2024 | for Version 2

Daniela Holtgräwe, Genetics and Genomics of Plants, CeBiTec and Faculty of Biology, Bielefeld University, Bielefeld, Germany

1 Views Cite this report Responses(0)

Approved With Reservations

There is a lot of progress on the manuscript in more or less all addressed points. There are still some problems with the Github entries. The provided link for the SNP calling data is wrong. The link needs to be changed to
https://github.com/tmlange/IFS_SNPpairs
As a person who supports the FAIR principles in the data analysis and publications, I cannot welcome that the actually relevant data, such as SNP positions in a reference genome or surrounding sequence information and genotype informations, can only be obtained after requesting the breeding company.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Plant genetics, crop genomics, computational biology, transcriptomics, genome assembly, gene annotation, RGAs, genetic mapping, genotyping

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

12 Views

17 Sep 2024 | for Version 2

Chenggen Chu, USDA-ARS, North Dakota, USA

12 Views Cite this report Responses(0)

Not Approved

The manuscript entitled "Improving genomic prediction of rhizomania resistance in sugar beet (Beta vulgaris L.) by implementing epistatic effects and feature selection" conducted genomic prediction for rhizomania resistance in sugar beet. However, I'm a little confused by the reports due to lack of sufficient information.
1) it's mentioned that a sugar beet population for this trial was developed by crossing two sugar beet lines, but no information about the two lines.
2) it's mentioned that homozygosity of Rz1 and Rz2 were determined using the SNP chip data. How was that determined? Is the accuracy for such determination 100%?
3) since this a population derived from two lines and thus is well structured, why not just use QTL analysis to determine resistance regions to see if resistance from Rz1, Rz2, or others? Genomic training and prediction are normally conducted using an association panel with lines from different families but not from a single cross.
4) for resistance evaluation, how many plants per genotype were used? what's the variation within each genotype?
I need all above information to provide further review to this manuscript.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

sugar beet genetics and breeding

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

28 Views

27 Sep 2023 | for Version 1

Daniela Holtgräwe, Genetics and Genomics of Plants, CeBiTec and Faculty of Biology, Bielefeld University, Bielefeld, Germany

28 Views Cite this report Responses(1)

Not Approved

In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
The programs on github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.

Is the work clearly and accurately presented and does it cite the current literature?

Partly
Is the study design appropriate and is the work technically sound?

Yes
Are sufficient details of methods and analysis provided to allow replication by others?

Partly
If applicable, is the statistical analysis and its interpretation appropriate?

Yes
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Plant genetics, crop genomics, computational biology, transcriptomics, genome assembly, gene annotation, RGAs, genetic mapping, genotyping

Respond to this report

Responses (1)

Author Response

28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

Reviewer Comment:
(1) In the introduction, the individual genes identified to confer resistance to Rhizomania should be mentioned and the underlying resistance mechanism, if known, should be briefly described. At least Rz2 is well studied in this regard. Two clusters are believed to exist on chr. 3. Associated genomic markers are known for each Rz locus, so that the physical distance of these genes can be specified on a reference sequence in addition to genetic distance in cM. Furthermore, it is not clear why the authors assume epistasis rather than additive effects between the genes involved.
Author Response:
We agree with the reviewer and have adjusted the introduction based on the recommendations of the reviewer. Furthermore, we have adjusted the Discussion section of the manuscript by adding a short discussion about epistasis and additive effects affecting rhizomania resistance.

Reviewer Comment:
(2) The description of the sugar beet population employed is incomplete. As a result, it is unclear which genetic material was used. A look at the authors list allows to speculate about the sugar beet genotype used for generating the population (Liebe et al., 2023; Wetzel et al., 2021). However, unequivocal specification of the material used is mandatory.
Author Response:
Unfortunately, the rights to the germplasm used in this trial are held by KWS Saat SE & Co. KGaA. We are therefore not in the position to publish this information. However, we have added a data availability statement to the manuscript stating that this information can be shared upon reasonable request.

Reviewer Comment:
(3) For the DAS-ELISA description the range of OD-values is missing. OD measurements were done 30, 60, and 90 minutes, but only data for the 90 min time point are provided. The authors should leave a comment, why they focused on the data obtained after 90 min of antibody exposure.
Author Response:
For the analysis, we have focused on the transformed data that were produced by transforming and averaging the ELISA measurements at all three time points. At the beginning of the results section, however, we have briefly described the OD measurements to show the range of the resulting OD values. Nevertheless, we agree with the reviewer that it is not clear why we have described the range of the OD values measured after 90 minutes and not after 60 and 120 minutes. Thus, we have added the range of the ELISA measurements after 60 and 120 minutes in the manuscript.

Reviewer Comment:
(4) Further, it is unclear from which experimental approach the SNP data were derived. Do the authors really mean SNP or SNVs? Where do missing values come from? What is the overall SNP frequency? These questions are also points that need to be taken up in the discussion.
Author Response:
We appreciate the reviewer's criticism and agree that the current version of the manuscript lacked detailed information about the SNPs. Additionally, the reviewer correctly pointed out that, prior to MAF filtering, we are actually considering SNVs, not SNPs. However, we would like to keep referring to the SNVs as SNPs to improve readability of the manuscript since the data were collected using a SNP chip.

Reviewer Comment:
(5) The programs on Github look very useful, but the data from the trial are not easily accessible due to limited documentation. Therefore, the documentation needs to be improved significantly.
Author Response:
We acknowledge the reviewer’s valuable feedback regarding the accessibility of the data from the trial on GitHub. We agree with the criticism and have significantly improved the documentation as requested. This should ensure that the data are now easily accessible and usable.

Reviewer Comment:
(6) In the methods section, is one of 155 and not of 156 genotypes susceptible to Rz2? Is this a typo?
Author Response:
This was indeed a typo and we have corrected the corresponding part of the manuscript.

Reviewer Comment:
(7) It would be easier to track the genotype, if the authors would provide a population name and a number or name for each individual in this population.
Author Response:
We have added genotype names for each individual in the data set on GitHub. Furthermore, we have given a special name for the genotype that was susceptible at Rz2 (``Control_susceptibleRz2'').

Reviewer Comment:
(8) For the feature selection “125 data points” were chosen for training data. These section needs to be re-phrased in order to make clear that SNP data from 125 genotypes (80% of individuals in population) at a certain recoded position was used.
Author Response:
We thank the reviewer for this very attentive comment and have adjusted the corresponding part of the manuscript.

Reviewer Comment:
(9) Very interesting is that a set of 29 SNPs each seems to have the highest predictive performance. The reader could certainly make more sense out of this observation if one or two of these different sets were shown as well as the overlap between all 1-10 sets.
Author Response:
Following the suggestion, we conducted an analysis to assess the overlap of the selected SNPs. Our findings revealed that four SNPs were consistently identified through this approach. Subsequently, we have integrated this information into the manuscript, highlighting that these four detected SNPs account for a significant portion of the total variance in the phenotypic data.

Reviewer Comment:
(10) The authors should discuss why they use genome wide SNP data and don't just use SNPs from chromosome 3 and therefore could require less computing power.
Author Response:
Thanks to the advice of the reviewer to analyse the overlap of selected SNPs, we discovered four SNPs that carry information about rhizomania resistance. In consultation with KWS Saat SE & Co. KGaA, we were allowed to publish the chromosomes on which these four SNPs are located. We show that two of the identified SNPs are not located on chromosome 3 but on chromosomes 2 and 5. We have included this new information in the manuscript which shows the importance of including SNPs from various chromosomes when examining SNP interactions.

Reviewer Comment:
(11) The second section of the discussion has a duplicated part to the results section. The same is true for the conclusion and the discussion, please rephrase and remove redundancy.
Author Response:
We appreciate the reviewer's feedback and acknowledge that the manuscript's writing style required enhancement. In response to the reviewer's criticism, we have refined the writing style of the manuscript to reduce redundancy in both the discussion and conclusion sections.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

33 Views

12 Sep 2023 | for Version 1

Muhammad Massub Tehseen, Department of Plant Sciences, North Dakota State University, Fargo, North Dakota, USA

33 Views Cite this report Responses(1)

Not Approved

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

No
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Sugarbeet genetics, genomics and breeding.

Respond to this report

Responses (1)

Author Response

28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

Reviewer Comments:
(1) First of all there is no clear description of the population panel used in the current study, the authors reported a panel of 156 genotypes followed by a cross and the progenies were advanced for two generations. It is very unclear as for what is happening, whether the 156 initial were used or the progenies derived from the cross? Why the crosses were made? The choice of parents and the reason or basis of selection? The authors assume the presence/absence of resistance which is not backed up by the variance in the phenotypic data generated. There should be detail description of the panel used, the experimental design, replications and phenotypic data generation.

Author Response:
We agree with the reviewer that the manuscript did not provide sufficient detail on how the sugar beet population in this trial was created. We have revised the corresponding paragraph to improve the clarity of the study.

Reviewer Comments:
(2) The genomic prediction (GP) for any trait relies heavily on the traits heritability values, here the authors have claimed the maximum GP estimates of .030 which is fairly below moderate however it is hard to conclude its reliability without judging the quality and heritability values of the traits under study. Therefore, authors’ are suggested to estimate heritability before reporting any conclusions.

Author Response:
It is important to clarify that our analysis focuses on the coefficient of determination (R²) rather than the correlation coefficient (r). R² is generally lower than r and represents the proportion of the variance explained by the model. In this context, the GP estimate of 0.30 suggests that a significant portion of the trait's variance can be explained by genomic information, demonstrating the potential of genomic prediction for this particular trait.

We agree that heritability estimates are crucial for assessing the reliability of GP and acknowledge the need to consider the quality and heritability values of the traits under study. Therefore, we concur with the reviewer's recommendation to include heritability estimates in future studies which would provide a more comprehensive understanding of the trait's predictability. In the current manuscript, our primary objective was to demonstrate the feasibility of genomic prediction for this trait, even with lower GP estimates. We believe that our results demonstrate potential in this area and we look forward to refining our analysis by incorporating heritability estimates in future research to strengthen our conclusions.

Reviewer Comments:
(3) The analysis was conducted without including SNP in LD with the two resistance genes which seems to be strange and requires clarification from authors as why it was done? If the presence of highly associated SNPs would skew the prediction results then they should be mentioned and in fact presented side by side for comparison. Furthermore, to avoid the prediction ability influence by the low number of cross-validation i.e. 5-fold in the current study, each method should have run at least 100 CVs. If not 50 instead of just 10. The 10 times iteration generally just gives a rough idea of the prediction accuracy for more reliable estimates there should be at least 50 iterations.

Author Response:
As thoroughly explained in the manuscript, each individual in the population is resistant at Rz1, with only one individual being susceptible at Rz2. The SNPs in high LD with the known resistance genes were not removed to skew prediction results. Instead, SNPs in high LD with Rz1 provide no variance and, thus, carry no useful information. The same applies to SNPs in high LD with Rz2, as they are identical for all but one individual in the population. Therefore, these SNPs were excluded in the minor allele frequency filtering step (MAF smaller than or equal to 0.05) which is standard practice to ensure minimum genetic variance in both the test and training data sets.

Regarding the second part of the criticism, the methods we used are computationally intensive, making it impractical to repeat the analysis 100 times as suggested. We employed a ten-fold repetition, consistent with similar research methodologies. For instance, Azodi et al. (2019) utilised this number of repetitions in their study on benchmarking parametric and machine learning models for genomic prediction of complex traits. As stated in the manuscript, our R script and data are publicly available and we encourage the reviewer or any interested party to replicate the study with a higher number of repetitions if desired.

Reviewer Comments:
(4) As for the revision of the manuscript, the authors should avoid the lots of repetition and use of assumptions in the text. In many instances the assumed statements could be verified easily. The authors are requested to re-submit the revised manuscript to be considered for indexing.

Author Response:
We appreciate the reviewer's criticism and agree that the manuscript's writing style required enhancement. We have revised the manuscript to improve the writing style, addressing the reviewer's concerns by reducing repetitions and clarifying assumptions.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

48 Views

28 Jul 2023 | for Version 1

J Mitchell McGrath, USDA-ARS Sugarbeet and Bean Research Unit, Michigan State University, East Lansing, Michigan, USA

48 Views Cite this report Responses(1)

Not Approved

Is the work clearly and accurately presented and does it cite the current literature?

No
Is the study design appropriate and is the work technically sound?

Partly
Are sufficient details of methods and analysis provided to allow replication by others?

No
If applicable, is the statistical analysis and its interpretation appropriate?

I cannot comment. A qualified statistician is required.
Are all the source data underlying the results available to ensure full reproducibility?

No
Are the conclusions drawn adequately supported by the results?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Genetics, genomics, and germplasm enhancement of sugar beet

Respond to this report

Responses (1)

Author Response

28 Aug 2024

Thomas Martin Lange, Breeding Informatics Group, University of Göttingen, Göttingen, 37075, Germany

Reviewer Comment:
(1) It seems that a study to dissect additional components of rhizomania resistance would include analysis of the rhizomania resistance genes. The authors state that the germplasm used were 'assumed' to carry the relevant genes Rz1 and Rz2 (in all but one of 156 entries) (gene symbols need to be italicized in publication). It is entirely unclear what material was used (presumably material initiating from KWS), with one statement suggesting 156 lines and, conversely, a following statement that two lines were crossed and selfed for two generations. Which of these are the population(s) for which the analyses were done? And if both, it needs to be made clearer in the text, as well as for what question each of the populations was used. A list of germplasm used should be included.

Author Response:
After revising the addressed paragraph, we agree with the reviewer's assessment. The paragraph describing the experimental design and, notably, the composition of the analysed population was overly complex and did not clearly articulate how the population was established. We have revised the paragraph to provide a clearer explanation of the population's creation and genotyping process.

Additionally, the reviewer raised concerns regarding the lack of naming for the initial two sugar beet lines used to create this population. We acknowledge that the rights to the germplasm utilised in this trial are held by KWS Saat SE & Co. KGaA, and as such, we are unable to disclose this information. However, in response to the reviewer's criticism, we have included a data availability statement in the manuscript and italicised the gene names.

Reviewer Comment:
(2) Analyses proceeded without using SNPs for the two named resistance genes, and I think this is a flaw in the logic of the paper. Evidence for the assumption that the germplasm is resistant is essential. Assuming the author's assumption is valid, the logic for excluding SNPs for Rz1 and Rz2 should be presented. I suspect there may have been a concern that the known genes with major effect may have overwhelmed the signal from discovered modifiers (the point of the manuscript), however this needs to be demonstrated. If this is the case, what are the implications for the 'strength' or 'effectiveness' of the discovered modifiers? Since the manuscript deals strictly with in silico investigations, it seems a relatively small matter to test the effect of named resistance genes on the results, and then exclude for cause if that is indeed the case.

Author Response:
We appreciate the reviewer's point regarding the importance of providing evidence for the assumption of germplasm resistance. Indeed, we have conducted an analysis of the resistance of the population at Rz1 and Rz2 using SNP markers. However, it is crucial to note that the SNPs in high linkage disequilibrium (LD) with Rz1 and Rz2 exhibit minimal genetic variance because all plants in the population are resistant at the two known resistance genes. Consequently, these SNPs do not contribute any meaningful information and are unsuitable for genomic prediction. Consequently, these SNPs were removed due to minor allele frequency filtering (MAF smaller than or equal to 0.05). We recognise that the omission of this information about the removal of SNPs in high LD with the resistance genes may has caused confusion, and we have thoroughly adjusted the Materials and Methods section of the manuscript to clarify this aspect.

Reviewer Comment:
(3) The author's writing suggests many assumptions were used in their analyses. It is difficult to interpret what is indeed a true assumption from a postulate they wish to have tested, so purging the manuscript for words relating to 'assume' would create better credibility for the work, unless it is absolutely essential (and even then with clear implication for their results if the assumption does not hold). (For many assumptions presented, relatively simple procedures can validate them, which may have been done in the course of the work.) Excluding SNPs with a major allele frequency of >0.95 seems arbitrary as well, although as above, it is difficult to ascertain the author's intent given the questions of the population(s) evaluated. So, in that respect, the manuscript can not be properly vetted yet.

Author Response:
We acknowledge the reviewer's feedback and have revised the manuscript accordingly. We acknowledge that the term "to assume" was overused, particularly when describing the "assumption" that the plants are resistant at Rz1 and Rz2. As detailed in the manuscript, the plants were analysed using SNP markers. All genotypes were homozygous for the resistance gene at SNPs in high LD with Rz1, and 155 out of 156 genotypes were homozygous for the resistance gene at SNPs in high LD with Rz2. However, we use the term "to assume" because LD does not provide absolute certainty that an individual carries the specified gene when the corresponding SNP marker shows a particular allele. Nonetheless, the reviewer's point is well taken, and we have adjusted the relevant sections to enhance the manuscript's readability.

Furthermore, the reviewer criticised the removal of SNPs with a major allele frequency of 0.95 or higher from the data set. This practice is common to ensure that each SNP contributes sufficient genetic variance in both the training and test populations. Therefore, we do not intend to alter this aspect of the method or the corresponding section of the manuscript.

Reviewer Comment:
(4) As suggestions for revision, clarity of writing for an audience is essential. Right now, this seems to be a draft that organizes the authors' thoughts into a manuscript format. Jargon should be avoided. Assumptions should be justified. Where available, actual numbers should be presented (rather than qualitative statements such as 'many', 'the remaining', etc.) to allow the reader to properly account for the process obtaining results. Concepts used should be defined (e.g. 'variable importance', 'technical limit', etc.). I would also like to see what genomic regions the author's have discovered and how the different methods/ algorithms differed with respect to the types of genes and elements discovered. Specifically, one needs evidence that this approach is likely to be successful. Or, if this is a manuscript describing negative results, that should be stated as well.

Author Response:
We appreciate the reviewer's feedback and agree that the writing style of the manuscript required improvement. We have revised the manuscript accordingly. Definitions of technical terms, such as variable importance and the technical limit of the machine, have been added for clarity. Additionally, we have included more information on the overlap in methods regarding the detection of important SNPs. In response to the reviewer's criticism, KWS Saat SE & Co. KGaA agreed to publish the chromosomes on which SNPs are located that were detected using our method. We have also added a data availability statement to the manuscript stating that the exact position on the chromosome as well as the genomic positions of the other SNPs in this data set are available upon reasonable request.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Řezbová H, Belová A, Škubna O: Sugar beet production in the European Union and their future trends. Agris on-line Papers in Economics and Informatics. 2013; 5(665-2016-44967): 165–178.

[2] 2. Draycott AP: Sugar Beet. 1st ed.New York: John Wiley & Sons; 2008. 978-1-405-17336-0.

[3] 3. Scholten OE, Lange W: Breeding for resistance to rhizomania in sugar beet: A review. Euphytica. 2000; 112(3): 219–231. Publisher Full Text

[4] 4. Tamada T: Beet necrotic yellow vein virus. CMI/AAB Description of plant viruses. 1975; 144: 1–4.

[5] 5. Giunchedi L, Giuchedi L, Langenberg WG: Beet necrotic yellow vein virus transmission by Polymyxa betae keskin zoospores. Phytopathol. Mediterr. 1982;5–7.

[6] 6. Ciafardini G: Evaluation of Polymyxa betae Keskin contaminated by Beet necrotic yellow vein virus in soil. Appl. Environ. Microbiol. 1991; 57(6): 1817–1821. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Özmen CY, Khabbazi SD, Khabbazi AD, et al.: Genome composition analysis of multipartite BNYVV reveals the occurrence of genetic re-assortment in the isolates of Asia Minor and Thrace. Sci. Rep. 2020; 10(1): 4111–4129. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Abe H, Tamada T: Association of beet necrotic yellow vein virus with isolates of Polymyxa betae Keskin. Japanese Journal of Phytopathology. 1986; 52(2): 235–247. Publisher Full Text

[9] 9. Biancardi E, Tamada T: Rhizomania. Springer International Publishing; 2016. Publisher Full Text

[10] 10. Broccanello C, McGrath JM, Panella L, et al.: A SNP mutation affects rhizomania-virus content of sugar beets grown on resistance-breaking soils. Euphytica. 2017; 214(1). Publisher Full Text

[11] 11. European Food Safety Authority (EFSA) Panel on Plant Health (PLH)Dehnen-Schmutz K, Di Serio F, et al.: Pest categorisation of beet necrotic yellow vein virus. EFSA J. 2020; 18(12). 18314732. Publisher Full Text

[12] 12. McGrann GRD, Grimmer MK, Mutasa-Göttgens ES, et al.: Progress towards the understanding and control of sugar beet rhizomania disease. Mol. Plant Pathol. 2009; 10(1): 129–141. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Koenig R, Lüddecke P, Haeberle AM: Detection of beet necrotic yellow vein virus strains, variants and mixed infections by examining single-strand conformation polymorphisms of immunocapture RT-PCR products. J. Gen. Virol. 1995; 76(8): 2051–2055. PubMed Abstract | Publisher Full Text

[14] 14. Tamada T, Shirako Y, Abe H, et al.: Production and pathogenicity of isolates of beet necrotic yellow vein virus with different numbers of rna components. J. Gen. Virol. 1989; 70(12): 3399–3409. Publisher Full Text

[15] 15. Harju VA, Mumford RA, Blockley A, et al.: The occurrence in the United Kingdom of Beet necrotic yellow vein virus isolates which contain RNA 5. New Dis. Rep. 2002; 51: 18–18. Publisher Full Text

[16] 16. Koenig R, Lennefors B-L: Molecular analyses of European A, B and P type sources of Beet necrotic yellow vein virus and detection of the rare P type in Kazakhstan. Arch. Virol. 2000; 145(8): 1561–1570. PubMed Abstract | Publisher Full Text

[17] 17. Heijbroek W, Musters PMS, Schoone AHL: Variation in pathogenicity and multiplication of beet necrotic yellow vein virus (BNYVV) in relation to the resistance of sugar-beet cultivars. Eur. J. Plant Pathol. 1999; 105(4): 397–405. Publisher Full Text

[18] 18. De Biaggi M, Stevanato P, Saccomani M, et al.: Sugar beet resistance to rhizomania: State of the art and perspectives. Sugar Tech. 2010; 12(3-4): 238–242. Publisher Full Text

[19] 19. De Biaggi M: Methodes de delection-un cas concret. Proceedings of IIBR 50th Winter Congress, 1987. Institut International de Recherches Betteravieres; 1987.

[20] 20. Lewellen RT, Skoyen IO, Erichsen AW: Breeding sugar beet for resistance to rhizomania: Evaluation of host-plant reactions and selection for and inheritance of resistance. 50. Winter Congress of the International Institute for Sugar Beet Research, Bruxelles (Belgium), 11-12 Feb. 1987. IIRB. Secretariat General. 1987.

[21] 21. Stevanato P, De Biaggi M, Broccanello C, et al.: Molecular genotyping of “rizor” and “holly” rhizomania resistances in sugar beet. Euphytica. 2015; 206(2): 427–431. Publisher Full Text

[22] 22. Scholten OE, De Bock TSM, Klein-Lankhorst RM, et al.: Inheritance of resistance to beet necrotic yellow vein virus in Beta vulgaris conferred by a second gene for resistance. Theor. Appl. Genet. 1999; 99(3-4): 740–746. PubMed Abstract | Publisher Full Text

[23] 23. Capistrano-Gossmann GG, Ries D, Holtgräwe D, et al.: Crop wild relative populations of Beta vulgaris allow direct mapping of agronomically important genes. Nat. Commun. 2017; 8(1): 1–8.

[24] 24. Gidner S, Lennefors B-L, Nilsson N-O, et al.: QTL mapping of BNYVV resistance from the WB41 source in sugar beet. Genome. 2005; 48(2): 279–285. PubMed Abstract | Publisher Full Text

[25] 25. Grimmer MK, Trybush S, Hanley S, et al.: An anchored linkage map for sugar beet based on AFLP, SNP and RAPD markers and QTL mapping of a new source of resistance to Beet necrotic yellow vein virus. Theor. Appl. Genet. 2007; 114(7): 1151–1160. February. PubMed Abstract | Publisher Full Text

[26] 26. Grimmer MK, Kraft T, Francis SA, et al.: QTL mapping of BNYVV resistance from the WB258 source in sugar beet. Plant Breed. 2008; 127(6): 650–652. Publisher Full Text

[27] 27. Lein JC, Asbach K, Tian Y, et al.: Resistance gene analogues are clustered on chromosome 3 of sugar beet and cosegregate with QTL for rhizomania resistance. Genome. 2006; 50(1): 61–71. Publisher Full Text

[28] 28. Olatoye MO, Hu Z, Aikpokpodion PO: Epistasis detection and modeling for genomic selection in cowpea (Vigna unguiculata L. Walp.). Front. Genet. 2019; 10: 677. PubMed Abstract | Publisher Full Text | Free Full Text

[29] 29. Cordell HJ: Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002; 11(20): 2463–2468. PubMed Abstract | Publisher Full Text

[30] 30. Mathew B, Léon J, Sannemann W, et al.: Detection of epistasis for flowering time using bayesian multilocus estimation in a barley MAGIC population. Genetics. 2018; 208(2): 525–536. PubMed Abstract | Publisher Full Text | Free Full Text

[31] 31. Carlborg Ö, Haley CS: Epistasis: too often neglected in complex trait studies?. Nat. Rev. Genet. 2004; 5(8): 618–625. PubMed Abstract | Publisher Full Text

[32] 32. Heinrich F, Ramzan F, Rajavel A, et al.: MIDESP: Mutual Information-Based Detection of Epistatic SNP Pairs for Qualitative and Quantitative Phenotypes. Biology. 2021; 10(9): 921. PubMed Abstract | Publisher Full Text | Free Full Text

[33] 33. Würschum T, Maurer HP, Schulz B, et al.: Genome-wide association mapping reveals epistasis and genetic interaction networks in sugar beet. Theor. Appl. Genet. 2011; 123(1): 109–118. PubMed Abstract | Publisher Full Text

[34] 34. Poland JA, Balint-Kurti PJ, Wisser RJ, et al.: Shades of gray: the world of quantitative disease resistance. Trends Plant Sci. 2009; 14(1): 21–29. PubMed Abstract | Publisher Full Text

[35] 35. St DA, Clair: Quantitative disease resistance and quantitative resistance loci in breeding. Annu. Rev. Phytopathol. 2010; 48: 247–268. Publisher Full Text

[36] 36. Bao Y, Vuong T, Meinhardt C, et al.: Potential of association mapping and genomic selection to explore pi 88788 derived soybean cyst nematode resistance. Plant Genome. 2014; 7(3). plantgenome2013–11. Publisher Full Text

[37] 37. Tiede T, Smith KP: Evaluation and retrospective optimization of genomic selection for yield and disease resistance in spring barley. Mol. Breed. 2018; 38(5): 1–16. Publisher Full Text

[38] 38. Roy J, Shaikh TM, del Río Mendoza L , et al.: Genome-wide association mapping and genomic prediction for adult stage sclerotinia stem rot resistance in brassica napus (l) under field environments. Sci. Rep. 2021; 11(1): 1–18. Publisher Full Text

[39] 39. Huang M, Balimponya EG, Mgonja EM, et al.: Use of genomic selection in breeding rice (Oryza sativa L.) for resistance to rice blast (magnaporthe oryzae). Mol. Breed. 2019; 39(8): 1–16. Publisher Full Text

[40] 40. Tomar V, Singh Dhillon G, Singh D, et al.: Evaluations of genomic prediction and identification of new loci for resistance to stripe rust disease in wheat (Triticum aestivum L.). Front. Genet. 2021; 12. PubMed Abstract | Publisher Full Text | Free Full Text

[41] 41. Ornella L, Pérez P, Tapia E, et al.: Genomic-enabled prediction with classification algorithms. Heredity. 2014; 112(6): 616–626. PubMed Abstract | Publisher Full Text | Free Full Text

[42] 42. González-Camacho JM, Ornella L, Pérez-Rodríguez P, et al.: Applications of machine learning methods to genomic selection in breeding wheat for rust resistance. Plant Genome. 2018; 11(2): 170104. PubMed Abstract | Publisher Full Text

[43] 43. Lange TM: IFS_SNPpairs.Feb 2023. Reference Source

[44] 44. Schirmer A, Link D, Cognat V, et al.: Phylogenetic analysis of isolates of Beet necrotic yellow vein virus collected worldwide. J. Gen. Virol. 2005; 86(10): 2897–2911. PubMed Abstract | Publisher Full Text

[45] 45. Lange TM, Wutke M, Bertram L, et al.: Decision Strategies for Absorbance Readings from an Enzyme-Linked Immunosorbent Assay—A Case Study about Testing Genotypes of Sugar Beet (Beta vulgaris L.) for Resistance against Beet necrotic yellow vein virus (BNYVV). Agriculture. 2021; 11(10): 956. Publisher Full Text

[46] 46. Clark MF, Adams AN: Characteristics of the microplate method of enzyme-linked immunosorbent assay for the detection of plant viruses. J. Gen. Virol. 1977; 34(3): 475–483. PubMed Abstract | Publisher Full Text

[47] 47. Lange TM, Rotärmel M, Müller D, et al.: Non-linear transformation of enzyme-linked immunosorbent assay (ELISA) measurements allows usage of linear models for data analysis. Virol. J. 2022; 19(1): 1–11. Publisher Full Text

[48] 48. Joiret M, Mahachie John JM, Gusareva ES, et al.: Confounding of linkage disequilibrium patterns in large scale DNA based gene-gene interaction studies. BioData Min. 2019; 12(1): 1–23. Publisher Full Text

[49] 49. Hartwig FP: SNP-SNP Interactions: focusing on variable coding for complex models of epistasis. J. Genet. Syndr. Gene Ther. 2013; 4(189): 10–4172.

[50] 50. Purcell S, Neale B, Todd-Brown K, et al.: PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007; 81(3): 559–575. PubMed Abstract | Publisher Full Text | Free Full Text

[51] 51. Azodi CB, Bolger E, McCarren A, et al.: Benchmarking parametric and machine learning models for genomic prediction of complex traits. G3: Genes, Genomes, Genetics. 2019; 9(11): 3691–3702. PubMed Abstract | Publisher Full Text | Free Full Text

[52] 52. Wright MN, Ziegler A: ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017; 77(1): 1–17. Publisher Full Text

[53] 53. Renaud O, Victoria-Feser M-P: A robust coefficient of determination for regression. J. Stat. Plan. Inference. 2010; 140(7): 1852–1862. Publisher Full Text

[54] 54. Haleem A, Klees S, Schmitt AO, et al.: Deciphering pleiotropic signatures of regulatory SNPs in Zea mays L. using multi-omics data and machine learning algorithms. Int. J. Mol. Sci. 2022; 23(9): 5121. PubMed Abstract | Publisher Full Text | Free Full Text

[55] 55. Segelke D, Chen J, Liu Z, et al.: Reliability of genomic prediction for German Holsteins using imputed genotypes from low-density chips. J. Dairy Sci. 2012; 95(9): 5403–5411. PubMed Abstract | Publisher Full Text

[56] 56. Kursa MB, Rudnicki WR: Feature selection with the Boruta package. J. Stat. Softw. 2010; 36: 1–13. Publisher Full Text

[57] 57. Ramzan F, Klees S, Schmitt AO, et al.: Identification of Age-Specific and Common Key Regulatory Mechanisms Governing Eggshell Strength in Chicken using Random Forests. Gen. 2020; 11(4): 464. Publisher Full Text

[58] 58. Klees S, Lange TM, Bertram H, et al.: In silico identification of the complex interplay between regulatory snps, transcription factors, and their related genes in brassica napus l. using multi-omics data. Int. J. Mol. Sci. 2021; 22(2): 789. PubMed Abstract | Publisher Full Text | Free Full Text

[59] 59. Bermingham ML, Pong-Wong R, Spiliopoulou A, et al.: Application of high-dimensional feature selection: evaluation for genomic prediction in man. Sci. Rep. 2015; 5(1): 1–12.

[60] 60. Sirsat MS, Oblessuc PR, Ramiro RS: Genomic prediction of wheat grain yield using machine learning. Agriculture. 2022; 12(9): 1406. Publisher Full Text

[61] 61. Chang C: Epistasis test - plink 1.9. Retrieved March 01, 2022, 2022. Reference Source

[62] 62. Winham SJ, Colby CL, Freimuth RR, et al.: SNP interaction detection with random forests in high-dimensional genetic data. BMC bioinformatics. 2012; 13(1): 1–13. Publisher Full Text

[63] 63. Wright MN, Ziegler A, König IR: Do little interactions get lost in dark random forests? BMC bioinformatics. 2016; 17(1): 1–10. Publisher Full Text

[64] 64. Shikha M, Kanika A, Rao AR, et al.: Genomic selection for drought tolerance using genome-wide snps in maize. Front. Plant Sci. 2017; 8: 550. PubMed Abstract | Publisher Full Text | Free Full Text

Improving genomic prediction of rhizomania resistance in sugar beet (Beta vulgaris L.) by implementing epistatic effects and feature selection

Abstract

Keywords

Introduction

Methods

Experimental design and data preparation

(1)

Genomic prediction and feature selection using single SNPs

Genomic prediction and feature selection using SNP pairs

Table 1. Recoding of two theoretical SNPs as well as the resulting SNP pair according to Ref. 49.

Results

Genomic prediction and feature selection using single SNPs

Figure 1. Median of the R2 values from the ten repetitions of genomic prediction using random forest with the 2, …, 9,127 SNPs.

Genomic prediction and feature selection using SNP pairs

Figure 2. Median of the R2 values from the ten repetitions of genomic prediction using random forest when the 3, …, 200 best single SNPs are combined to SNP pairs.

Discussion

Conclusions

Data availability

Underlying data

Extended data

Acknowledgements

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated

Figure 1. Median of the $R^{2}$ values from the ten repetitions of genomic prediction using random forest with the 2, $\dots$ , 9,127 SNPs.

Figure 2. Median of the $R^{2}$ values from the ten repetitions of genomic prediction using random forest when the 3, $\dots$ , 200 best single SNPs are combined to SNP pairs.