Keywords
Systems biology, bioinformatics, computational biology, machine learning, maximum entropy method, Bayesian statistics, RNA binding proteins, RNA Bind'n'Seq
This article is included in the Bioinformatics gateway.
We develop a thermodynamic model describing the binding of RNA binding proteins (RBP) to oligomers in vitro. We apply expectation-maximization to infer the specificity of RBPs, represented as position-specific weight matrices (PWMs), by maximizing the likelihood of RNA Bind’n Seq data from the ENCODE project. Analyzing these public data we find sequence motifs that can partly explain the data for more than half of the studied 111 RBPs, and for 48 of the proteins these motifs are consistent with the known specificity. Our code is publicly available, facilitating analysis of RBP binding data.
Systems biology, bioinformatics, computational biology, machine learning, maximum entropy method, Bayesian statistics, RNA binding proteins, RNA Bind'n'Seq
Following the suggestion of Johannes Söding, we reduced the degree of the Markov model to compute the sequence frequency priors. Consequently, we could confirm a lot more binding motifs obtained from our model with data from other sources. Therefore, we decided to expand the application of our model from just a few examples of public RNA Bind'n Seq data sets (RBFOX2, CELF1, hnRNPD, hnRNPK, MBNL1, hnRNPL, FUS, TAF15) to the entirety of publicly available Bind'n Seq data sets (111 RBPs in total on ENCODE). As a result, the run statistics are much more comprehensive (Fig. 1), and we added (Fig. 2) as a comparison of binding affinities and the respective motifs. Beyond that, we expanded the number of discussed RBP examples (Subsec. 4.1-4.14, Fig. 3-15). A derivation of relative binding affinities from our model terminology is appended to Sec. 2 and serves as a measure of comparison between PWMs of different length instead of the previous BIC and AIC. Following the suggestions of the reviewers, we clarified the derivation of the model (Sec. 2) and the EM procedure (Subsec. 3.2). We reflect the changes to our work in slight changes in the abstract to highlight the different outcome compared to version 1. We removed Appendix A since a list of used data sets is anyway given in the metadata of the article.
See the authors' detailed response to the review by Jun Zhang
See the authors' detailed response to the review by Johannes Söding
RNA-binding proteins (RBPs) interact with RNAs at every step of their life cycle. Due to their modular structure, usually consisting in an assortment of RNA-binding domains, RBPs interact with both RNAs and proteins, and couple various layers of gene expression.1 While RBPs are currently known, most remain to be functionally characterized. A first step in this process is to determine the interaction partners and the sequence/structure specificity of the RBP. Many RBPs recognize their targets in a sequence-specific manner, although the accessibility of binding sites within the targets also plays a role.2 The sequence specificity is usually represented by a position weight matrix (PWM), which specifies the probability of finding each of the four nucleotides at each position in the RBP binding site. This is an obvious simplification, as dependencies between positions in the binding site likely occur. However, training more complex models requires substantially more data, which are often not available. Moreover, in the case of another class of nucleic acid binding proteins, transcription factors, the improvement in binding site predictability by more complex models is modest, at least in the case of other nucleic acid binding proteins, transcription factors.3 With the realization that the presence of a canonical RNA-binding domains is not necessary for the ability of a protein to bind RNAs4 came a pressing need to determine the determinants of RNA-RBPs interactions and the sequence/structure specificity of the proteins newly found to interact with RNAs.
The past two decades have seen the development and broad application of experimental methods for RBP target identification. They include in vivo high-throughput approaches such as HITS-CLIP, PAR-CLIP, iCLIP and eCLIP (reviewed in Refs. 5, 6), and more recently-developed in vitro approaches such as RNA Bind’n Seq.7 While the CLIP methods rely on the sequencing of RNAs that interact with and can therefore be crosslinked to RBPs in vivo, RNA Bind’n Seq relies on the affinity-dependent interaction of RBPs with random RNAs in vitro. The oligonucleotides selected in this experiment are computationally analyzed to identify short sequence motifs that mediate the interaction with the RBP. So far, analyses of such data involved the identification of enriched kmers (short oligonucleotide sequences of a specified length, ), and then a greedy alignment procedure yielded PWM representations of the RBP binding motifs. This left open the question of whether the derived PWMs accurately predicted the interaction energies of RBPs with their binding sites. In contrast, the aim of our work was to develop a biophysics-anchored method to directly infer the PWMs from RNA Bind’n Seq data. Our paper is organized as follows: Sec. 2 explains how we derive our thermodynamical model. We comment on the practical implementation of this model in Sec. 3, where we also explain how we account for sequence composition biases in the pool of oligomers. Results for different RBPs are presented in Sec. 4, where we also comment on the accuracy of the results obtained from this type of data for different RBPs. Concluding remarks are given in Sec. 5.
Our model is an adaptation of a Bayesian, thermodynamic model that was constructed to infer di-nucleotide weight tensors from SELEX data.8 In the following, we derive the log-likelihood of Bind’N Seq data given the PWM for the RBP of interest, which will be inferred by expectation-maximization as described in Sec. 3.
We assume that an RBP binds an oligomer over a binding site of length and that the likelihood of binding taking place, according to Boltzmann’s law, goes as , where is the nucleotide at position , so . Therefore, each element of the position weight matrix (PWM) can be identified with , with columns being normalized as .
Additionally, we account for the fact that there are genuinely two different ways of binding, sequence-specific binding as described by the PWM, and unspecific binding to RNAs with a probability . Combining these two possibilities, we arrive at the probability of a site being bound by the RBP
Consequently, the chance of an RBP being bound somewhere on a longer oligomer with is
Eventually, the log-likelihood of the entire library of oligomers explained by the specific binding to the RBP described by the PWM of length as well as unspecific binding described by parameter is given by
The log-likelihood of binding derived in the previous section can be related to the dissociation constant known from the formalism of chemical reactions as follows. The concentration of RBP bound to a multivalent oligomer with concentration is given by9
Further assuming that the probability to observe individual oligomers in the sequencing pool is proportional to their relative abundance in complex with the RBP (which can only hold when at most one RBP molecule is bound to an individual oligomer), i.e. , we can re-express (2.5) in terms of (2.6) as
Hence, we can rank interactions by the dissociation constants relative to some reference PWM and
As expected, the result corrects for the library size-dependence of by dividing by the total foreground reads , and for differences in binding domain or read length by the last term. Assuming a random oligomer of length for which there is no unspecific binding () as reference allows us to bring into the simple closed form
Combining (2.9) with (2.5), the output of the optimization procedure, and the reference (2.10) allows us to compute the logarithm of the dissociation constant of the RBP-RNA binding for a representative RBP binding site relative to a random oligomer of length , a typical size for an RBP binding site. Relative ’s also provide a measure to rank different binding specificities, even of different lengths, for a given RBP.
Our goal is to identify the parameters that maximize the likelihood of the library of oligomers given in (2.5). This is equivalent to optimizing , or rather its logarithm to avoid underflows. While the library , the copy number of a read , the read and binding site lengths and , and – with some limitations – the frequency priors are given from our data, the position-specific binding of the RBP described by the PWM and the position-unspecific binding described by have to be inferred. Eventually, we want to obtain the PWM, whereas represents a hidden parameter which will be inferred via the expectation-maximization procedure. In principle, this would also apply to the concentration but none of our final expressions depend on any more due to linearization. Before diving into the details of the EM procedure’s implementation we would like to comment on how to infer the frequency priors .
RNA Bind’n Seq data does not only comprise libraries of reads pulled down by specific RBPs at non-vanishing RBP concentrations, but also libraries of input reads. The oligonucleotides that were used for RBP affinity-based selection were short, typically 20 nucleotides in length (c.f. Ref. 10). The number of possible 20mers is , much larger than the library sizes of . Thus, even in the absence of selection (), the expected overlap of two libraries is extremely small.
To preserve the statistical power of the foreground pool, i.e. use all the reads detected in the foreground sample in the analysis, even though they were not represented in the background sample, we have to predict the frequency of foreground reads under the assumption of no selection for binding the RBP. A commonly used approach for this type of problem is to train a Markov model from the background pool and construct the expected frequency of each read in the foreground from the trained model, just as in Ref. 11. For an completely unbiased process of oligomer synthesis, capture and sequencing the degree of the Markov model would be , i.e. each base would be equally likely to occur at any position in the oligomer, and all 20mers would have the same prior frequency of occurrence . However, various types of biases can lead to some sequences, with specific composition of short nucleotide motifs, being present in the data more often than others. In principle, the higher the degree of the Markov model, the larger the sequence context that can be resolved. However, an over-parametrization of the Markov-model needs to be avoided. As binding specificities of RBPs tend to be short and our main aim is to appropriately detect enrichment of motifs on this length scale, we used a Markov model of , which seemed to give a good tradeoff between the accuracy of the background read frequency prediction, size of Bind’n Seq libraries, and available compuational resources. The predicted frequency priors – and kmer-frequencies, accordingly – need to be normalized such that their sum over the background frequency pool satisfies .
Having constructed our model with the final expression (2.5), as well as the background frequencies described in the subsection above, the remaining task is to identify the PWM and maximize the log-likelihood (2.5). To this end, we rely on the expectation maximization algorithm.12,13 Provided that only some of our model parameters can be directly inferred from the data, the algorithm optimizes the”hidden” parameters to maximize (2.5). The expectation-maximization procedure (EM) can be divided into the following steps:
1. Initialize and the PWM elements with respectively well-defined real numbers, i.e. and . This can either be done in an entirely unbiased way or by pre-determining some motifs and initializing PWMs with values reflecting those motifs.
2. Recalculate to maximize (2.5) holding the PWM fixed, which amounts to finding the root of
We employ a Brent minimization algorithm from the GSL library14 to the negative value of the log-likelihood in (2.10) to maximize it.
3. Updating the PWM with the new from the previous step, splitting the data set into -mers (on a read ) and adding the weight
4. Repeat the previous two steps until convergence. We terminate the iteration when the quadratic difference between the current and the updated PWM is less than on average per entry, i.e. for the quadratic difference is less than . Usually, this takes iterations.
Our code is written in C++ and python and is publicly available.15
We analyzed all RNA Bind’n Seq data available in ENCODE10 for 111 RBPs. For each RBP, we investigated 11 different binding site lengths, nts, where the lower limit was chosen as in agreement with the literature, and the upper limit of nts was determined by the available RAM. Moreover, as most reads are nts long, a larger approaching this value would also not be warranted. For each of pair of RBP and , we set up 16 runs with randomly initialized parameters and 4 runs in which the initial PWM was set close to the reported consensus motif (from RBP Bind’n Seq data).10 We generally used four CPUs with three hours of maximum walltime per RBP, and eight CPUs when necessary (e.g. because the read length was larger than nts. For the overwhelming majority of runs we found these resources to be sufficient, though a few runs did not complete during this time, thus not all RBPs had exactly the same number of finished runs. Figure 1 gives an overview of the run statistics. As a local minimum was not found in all randomly initialized runs, the figure shows the fraction of “convergent” runs, i.e. runs in which the final log-likelihood was larger than the initial one. In addition, we observed that even convergent runs were sometimes dominated by the unspecific binding term . Since in this case the inferred PWM is not meaningful as it does not explain the data as well as the sequence-unspecific term, we report the “specific” cases, where . As shown in Figure 1 all RBPs with a large fraction () of convergent runs, led to the recovery of a specific motif. In contrast, RBPs with a low fraction () of convergent runs had solutions dominated by unspecific binding.
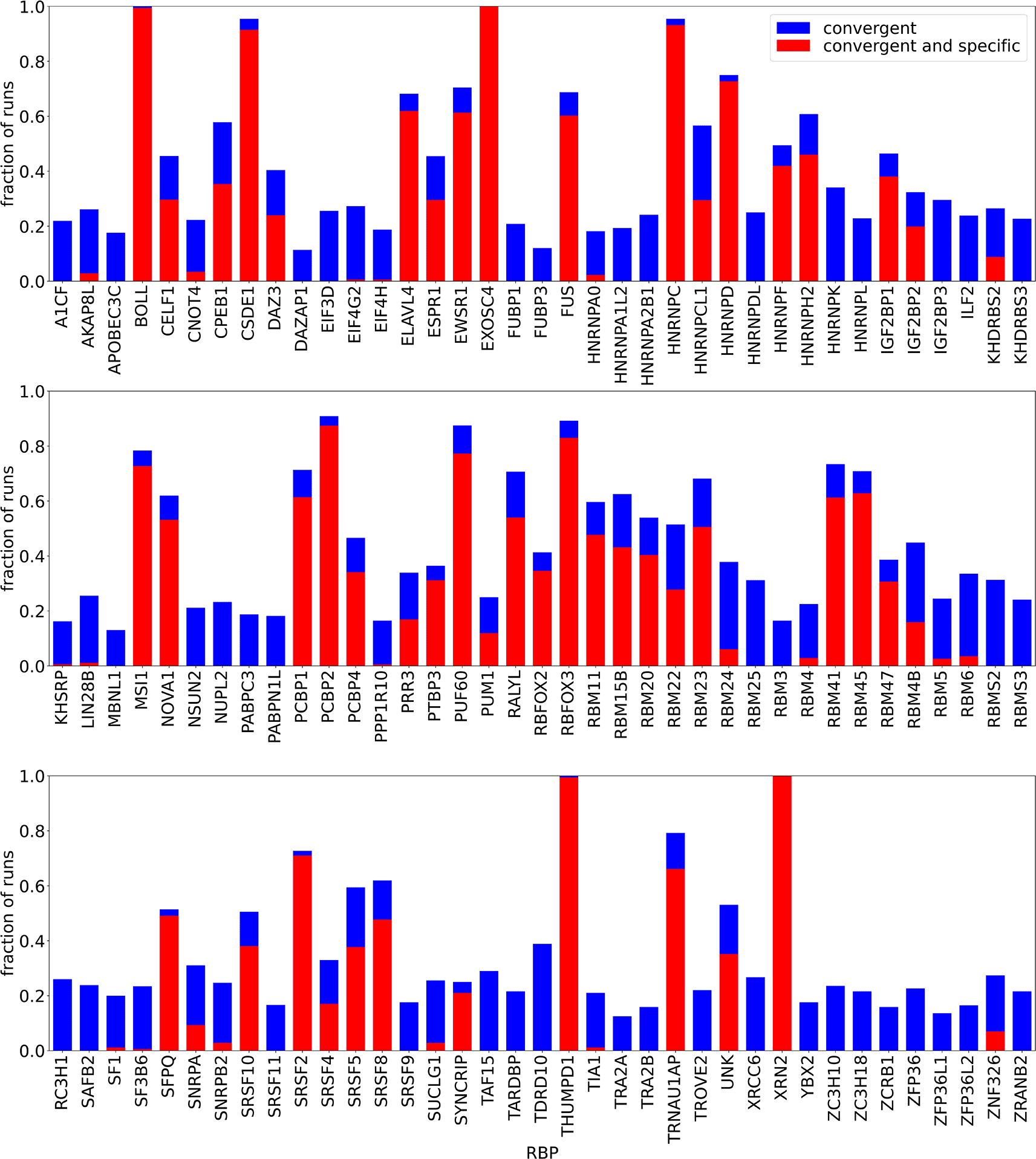
“Convergent” means that the final log-likelihood was larger than the initial one, “specific” means that , i.e. the non-specific binding term has a limited contribution to the overall energy of RBP-oligomer interaction. Some runs did not finish within the given maximum walltime, therefore the absolute numbers of runs was not exactly the same for all RBPs. All runs done for a given RBP, regardless of the are shown together.
Following eq. (2.9), we calculated the dissociation constants s for all convergent and specific outcomes of the EM procedure. Dissociation constants were given relative to a PWM of length , with equal probabilities for all four nucleotides () disregarding unspecific binding i.e. . This allows us to compare the binding strength of different motifs for an RBP with each other and also of motifs for different RBPs, as done in Figure 2. Below we highlight the motif and relative s for the motifs with the lowest and highest from random initialization, as well as the motif with the lowest obtained by initializing with the consensus PWM provided for the respective RBP by Ref. 10. As a first plausibility check, we find that longer motifs tend to have lower s, i.e. higher binding affinities, which is expected due to the larger number of bonds the larger binding sites can form with the RBP. We found convergent and specific results in 82 of 111 cases. Comparing the lowest motifs to the ones obtained by starting from the motifs found by kmer-enrichment analysis,10 we found that the consensus motif is contained in or differs in at most one position in 48 cases. 19 of the highest affinity motifs did not contain the ENCODE consensus; in 17 of these cases our algorithm found a less complex motif (mostly poly(A)), while in two cases (for CPEB1 and EIF4H) the motifs found by our algorithm are more complex. In 14 cases, the motif found by our algorithm appeared related to the consensus, but it was less polarized or differed from consensus in more than one position. For one RBP, PTBP3, no motif was reported based on RNA Bind’n-Seq data, while we found a convergent and specific poly(A) motif. The seemingly large bias towards poly(A) in case of no other motif found is consistent with adenine being the most prominent nucleotide in all of the investigated libraries.
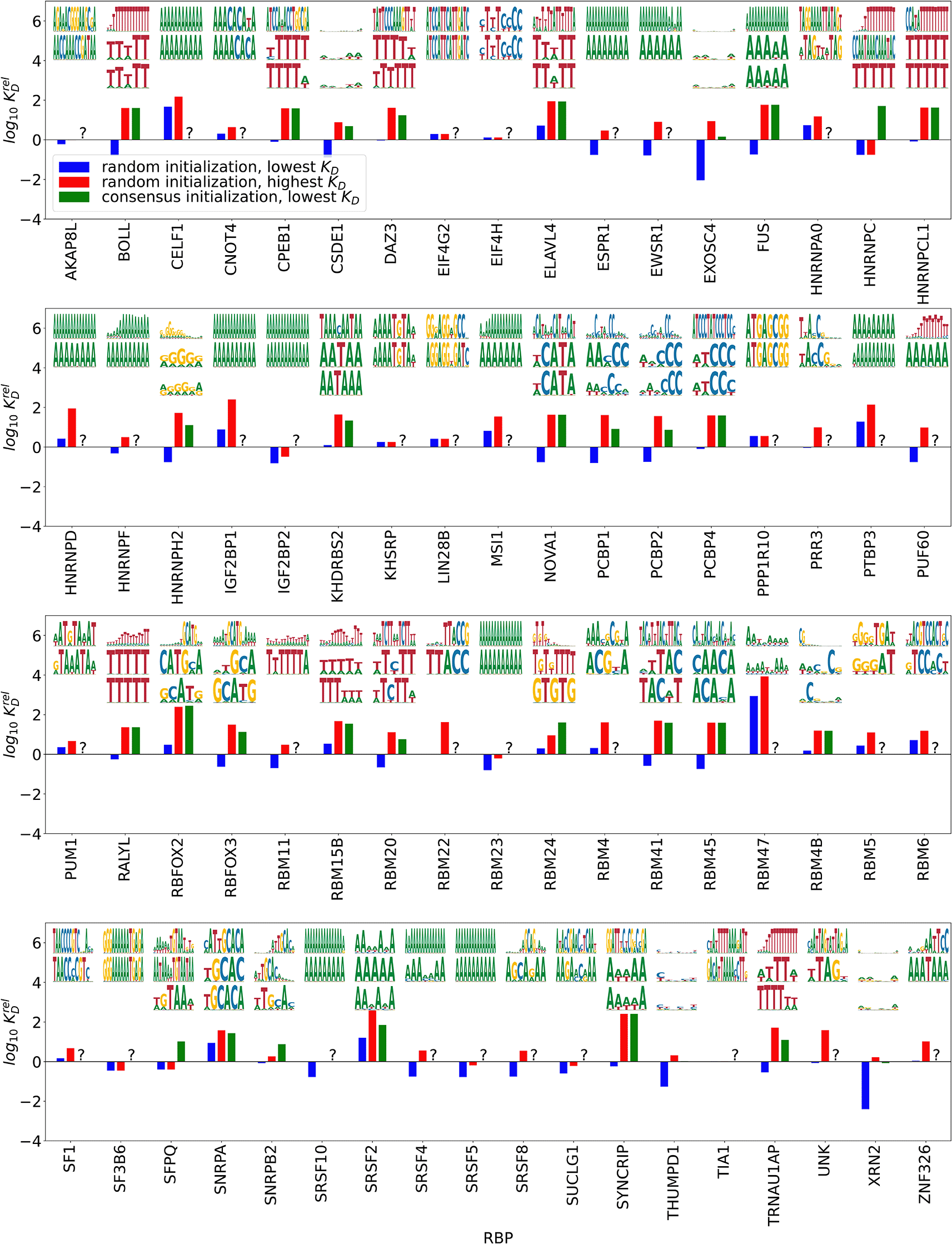
’s are relative to an unpolarized PWM of length 5 with no unspecific binding. Top/middle: highest/lowest affinity motifs (lowest/highest relative ) from random initialization, bottom: highest affinity motif from initializations with the consensus motif.
Below we assess the correspondence of the results given by our model with prior knowledge for a few proteins that have been extensively studied. Examples where we found motifs consistent with prior literature are RBFOX2, NOVA1, PUM1, PUF60, ELAVL4, hnRNPC, and PCBP1. In contrast, for CELF1, EWSR1, hnRNPD, and hnRNPK we either did not obtain a convergent and specific result or the result was clearly different from the reported consensus. We also discuss CPEB1, EIF4H, and PTBP3 as cases where our model appears to deliver new information. Note that as we start our analysis from sequenced DNAs we use T in the sequence logos, though of course, the RNA oligonucleotides contained U’s.
RBFOX2 is a key regulator of alternative splicing16 that was extensively studied with a variety of methods (e.g. Ref. 17). The RBFOX2 Bind’n Seq dataset10 consists in nine libraries obtained using nine different protein concentrations and two protein-free control libraries, all containing reads of nucleotides (nts) in length, including the adaptor. RBFOX2 is widely used to benchmark computational analysis methods (c.f. Ref. 18) and thus the corresponding dataset was carefully generated, to include multiple, high-quality libraries. Established techniques like kmer-enrichment analysis and the streaming-kmer-algorithm (SKA) predict a consensus 6mer TGCATG as the most prominent motif followed by other GCATG-containing 6mers.18 Our results in Figure 3 reproduce the importance of the GCATG morif, but also the slight T bias at the preceding position, see Figure 3(A). Moreover, we find the subdominant PWM Figure 3(B) which shares a CATG core with the highest affinity motif, but over-emphasizes the A bias downstream. These results demonstrate that our algorithm identifies the known consensus for RBFOX2.
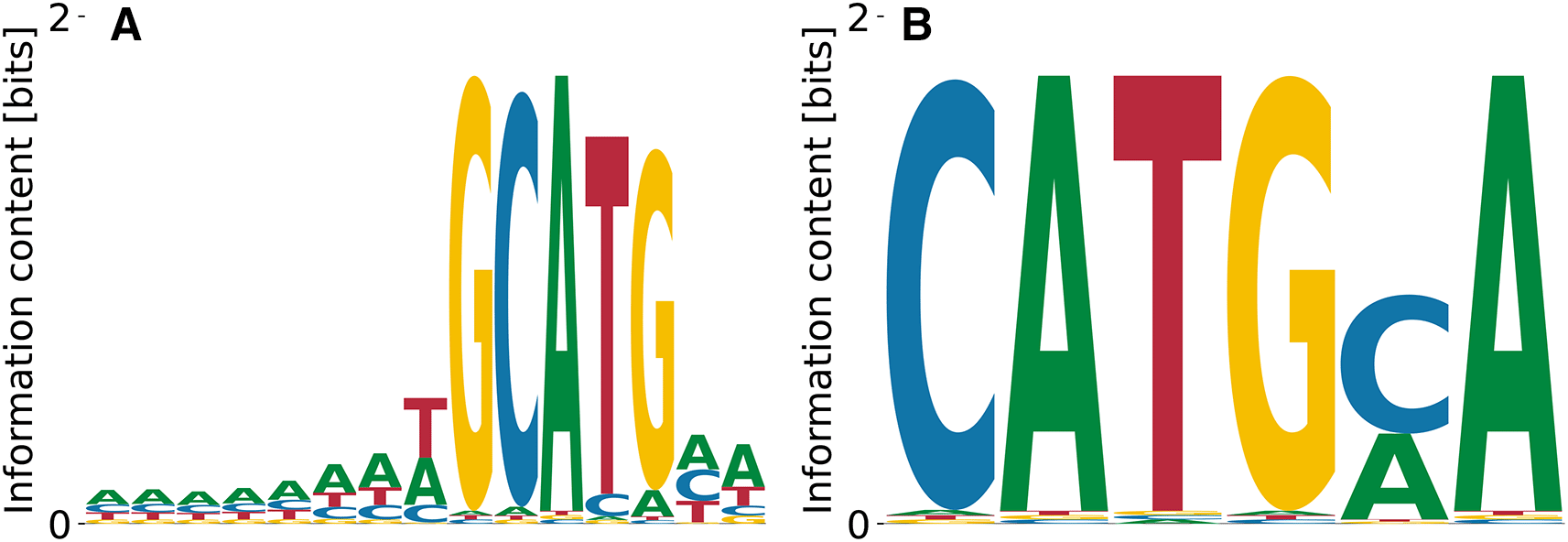
The highest affinity motif contains the known consensus GCATG, flanked by positions with low A/T bias. Both high and low affinity motifs share a CATG core.
The log-values of relative ’s are in the range - , meaning that the two motifs shown in Figure 3(A) and (B) differ by fold in their . The unspecific binding term in the run that yielded the motif from panel (A) was , while the one from the panel (B) run was . The overall log-likelihoods of the dataset were vs. , respectively. Thus, the higher affinity motif corresponds to a higher peak in the likelihood landscape, and accounts for a more specific interaction. The binding specificity of RBFOX2 in Figure 3(A) is similar to that of the closely related RBFOX3 (c.f. Figure 2).
The neuro-oncological ventral antigen 1 (NOVA1) is a neuron-specific RBP19 found by SELEX experiments to bind a triple CAT-repeat.20 This is confirmed by the motif identified by our algorithm (Figure 4). In contrast, the streaming kmer-enrichment analysis of RNA Bind’n Seq data in ENCODE predicted a single CAT.10
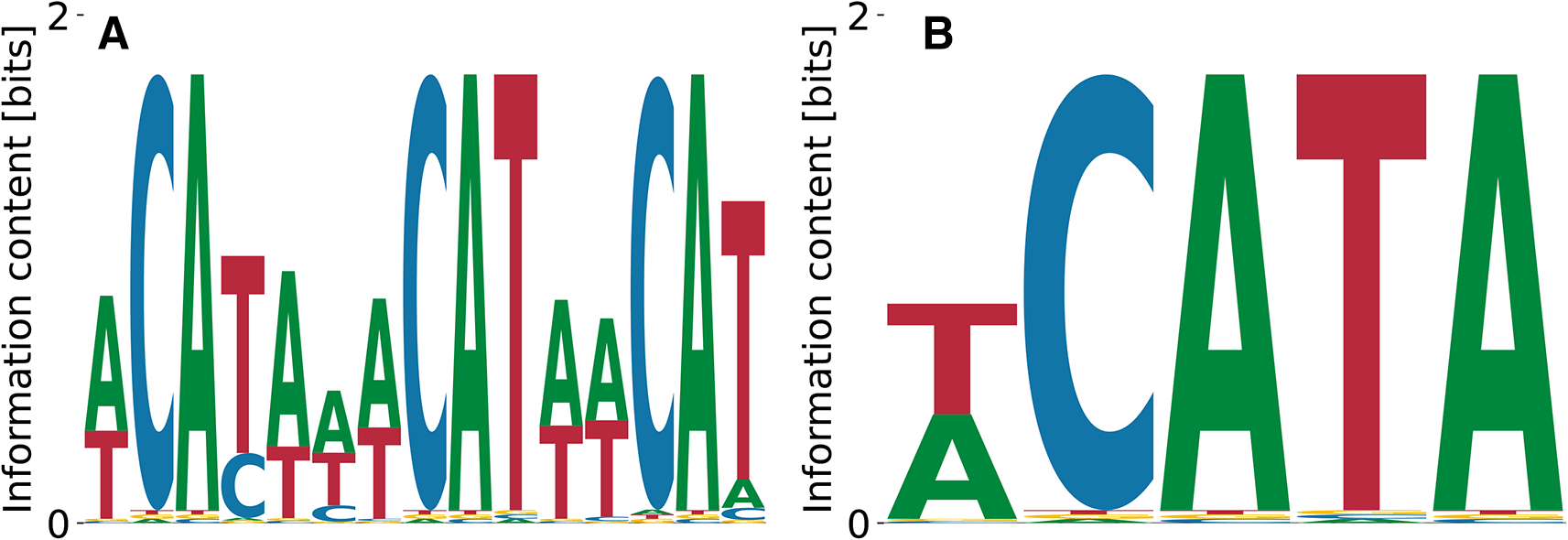
(A) shows the characteristic triple CAT-repeat.
Relative log- values ranged from to , the unspecific binding term was for Figure 4(A) and for Figure 4(B), and the log-likelihoods of the data were and , respectively.
Pumilio homolog 1 is a well-studied member of the PUF famility of proteins, which binds to 3’UTRs of a variety of mRNAs and regulates their translation.21 While immunoprecipitation (IP) experiments found its binding specificity to be TGTAHATA,22 SKA analysis of RNA Bind’n Seq yielded TGTAH without further context.10 In contrast, we do find the full motif in the Bind’n Seq data (Figure 5). All obtained motifs are related to each other via shifts and show only gradual differences at single positions, which also reflects in characteristic numbers (, , and ) being distributed only over a narrow range. The relative log-dissociation constants for Figure 5 are , , and , where the former two differ by only . The corresponding unspecific binding strengths are , , and . The log likelihoods of the data range from to .

The intermediate motif (B) represents the consensus.22
A representative from the same family of RBPs is the Poly(U)-binding splicing factor PUF60,23 which regulates both transcription and translation.24 Our algorithm finds the expected motif (poly(T)) as having the highest affinity Figure 6(A). The relative log- values for T-rich motifs are , with and . Different variations (see Figure 6(B)) of the poly(T) motif are found, having in common the alternating pattern of very polarized – less polarized T (the latter blended with C). Poly(A)-containing motifs (c.f. Figure 6(C)) also appear at and , with . The motif with the highest dissociation constant obtained from random initializations is shown in Figure 6(C), has , and corresponds to and .
The ELAV-like protein 4 (ELAVL4) is an RBP that is exclusively expressed in neurons.25 It binds A/T-rich elements according to genome-wide IP experiments,26,27 a pattern that we also observe in PWMs from our model (see Figure 7). Relative log-’s range from to , unspecific binding strength from to , and the log-likelihood of the data from to .
Turning towards another large familiy of RBPs, the heterogeneous nuclear ribonucleoproteins (hnRNPs), we highlight hnRNPC,28 a protein that is involved pre-mRNA processing.29 It is known to bind to poly(U) motifs, typically pentamers, found in both SKA analysis of RNA Bind’n Seq data10 and in electrophoretic mobility shift assays.30 Our model does recover the dominant poly(T) motif at , , and . Mildly subdominant motifs are A-rich and less repetitive (Figure 8(B), (C)) with , , and , as well as , , and .
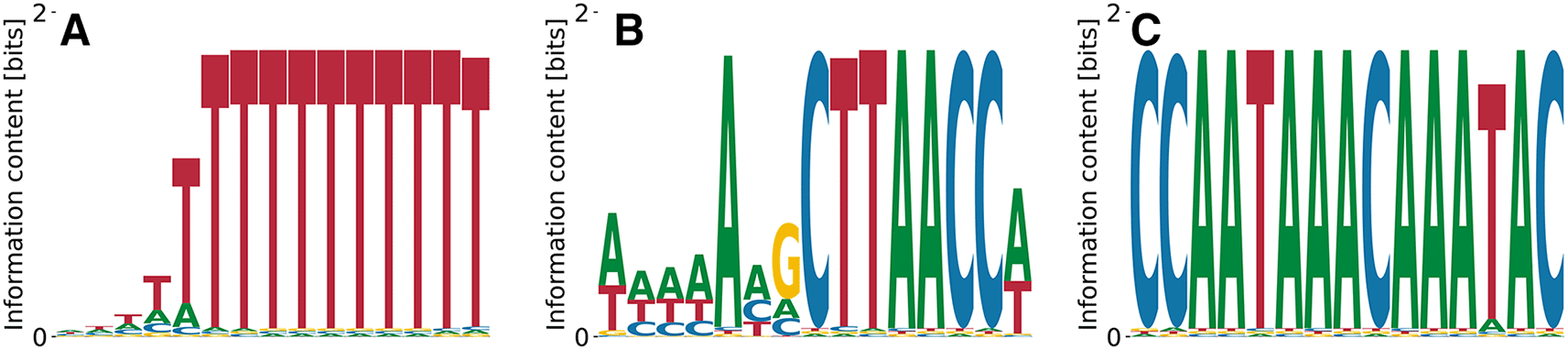
As a last example of RBPs of which we predict a motif that agrees with prior data, we highlight the poly (rC)-binding protein 1 (PCBP1).31 Its binding specificity consists of a few very polarized C’s linked by A/T-enriched sequence.32 This pattern is clearly reproduced by our highest affinity motif in Figure (9)(A) () with and . The lowest affinity motif (Figure 9(B)) that random PWM-initialization yielded had , , .
CELF1 is an RBP of the CUG-binding CELF family,33,34 that participates in multiple steps of post-transcriptional processing of RNAs, including splicing, translation and decay.35 CELF1 requires UGU motifs for high-affinity interaction with RNAs.36 The corresponding Bind’n Seq dataset10 consists of libraries generated for seven different RBP concentrations, each containing reads of .
Since runs with completely random PWM intialization for did not yield any local optimum of the probability landscape we decided to test whether the biased initialization of the PWM with the known motif (TGT), which was found as as enriched 3-mer in RNA Bind’n Seq10 enables the recovery of longer motifs. However, our model predicted only poly(A) stretches as convergent optima of the probability landscape, see Figure 10(A). The relative log-dissociation constants were , unspecific binding was characterized by , and the likelihood of the daat was between and .
EWSR1, or Ewing’s sarcoma protein, forms fusions with a number of other proteins and serves as a transcriptional activator in human solid tumors like Ewing’s sarcoma and malignant melanoma.37 Information about its binding specificity is scarce, while SKA analysis of RNA Bind’n Seq data predicts G-rich elements.10 Our investigation lead to different varieties of poly(A) motifs (Figure 11(A) and (B)), which vary in relative dissociation constants in log-, unspecific binding energy , and data likelihoods .

Enrichment analysis suggests a prominent as consensus, which our model cannot recover, even when initializing with .
Within the class of heterogeneous ribonucleoproteins (hnRNPs), hnRNPD (also known as AUF1) is a well-known A/U-rich element RNA binding protein with important role in RNA decay.38 HNRNPD has been reported to bind clusters of AUUUA elements.38 The ENCODE-database10 lists AUAAU as another possible binding site for hnRNPD. We find poly(A) stretches of different lengths as convergent and specific binding motifs (see Figure 12). While A is the dominating nucleotide at every position, it is followed consistently by T, which fits the reported A/U-rich binding domains in the literature. We find unspecific binding terms in the range , where Figure 12(B) corresponds to the highest affinity motif (Figure 12(A)) for which . The two motifs shown in Figure 12 come from a range of dissociation constants and data likelihoods . Direct initialization with the kmer-enrichment consensus ATAAT did not lead to any convergent and specific result.
We were also interested in determining whether we can recover G/C-rich binding motifs from the data and therefore applied the model to heterogeneous nuclear ribonucleoprotein K (hnRNPK), a member of the poly(C) binding family of proteins.39 We could only recover one of the two consensus motifs reported in the ENCODE analysis of these data (GCCCA, from SKA)10 when specifically initializing the PWM with this motif. The second reported motif, with the CACGC consensus, could not be found by our algorithm even when the PWM was initialized with the motif itself and even when sequences containing the first motif were eliminated, indicating that this motif does not correspond to a local maximum of the likelihood function. We did not find any PWMs of in this data set, whether we used random initialization or shorter motif-guided initialization.
The cytoplasmic polyadenylation element-binding protein 1 (CPEB1)40 serves as a translational regulator by binding specific U-rich sequences in 3’UTRs inducing cytoplasmic adenylation. The streaming kmer algorithm predicts a poly(T) motif from RNA Bind’n Seq data, which is what we recover as the lowest affinity motif in Figure 13(D) with , , and . The penta(T) is also part of a higher affinity motif (see Figure 13(C)) with , , and . More complex motifs with higher affinity, but less specificity are displayed in Figure 13(A) with , , and and in Figure 13(B) with , , and . While the difference in affinity between the first three motifs shown in Figure 13(A-C) is negligible, while the penta(T) motif alone (Figure 13(D) differs from the highest affinity one by -fold, which is quite substantial.
As a representative of the family of eukaryotic translation initiation factors, we highlight the eukaryotic translation initiation factor 4H (EIF4H).41 SKA enrichment studies of RNA Bind’n Seq data predict a poly(G) motif for this protein,10 but we did not find corroborating data obtained with other approaches. Our model identified only one convergent and specific motif shown in Figure 14, which is pyrimidine-rich. The relative log- is relatively high, , as is the contribution of unspecific binding, . .
Polypyrimidine tract-binding protein 3 (PTBP3) is involved in the regulation of numerous steps of protein production, i.e. splicing, alternative 3’ end processing, mRNA stability and RNA localization.42 Data on PTBP3 binding specificity is lacking, and enriched kmer was reported by the SKA from RNA Bind’n Seq data.10 Our model predicts different variations of poly(A), see Figure 15. The predicted binding specificities with the lowest features , , and . The motif corresponding to the highest had , , and . Thus, compared to other RBPs (c.f. Figure 14), the specificity of PTBP3 remains to be better defined.
There are other proteins covered in the Bind’n Seq data10 whose specificity was studied before. For example, we analyzed the data corresponding to MBNL1,43 hnRNPL,44 FUS,45 TAF15.46
Random and consensus intialization did result in convergent and specific binding specificities for FUS, however, these were poly(A) motifs which do not agree with the GGUG consensus from SELEX experiments.47 For the other threee proteins our model did not deliver any convergent results, even when the PWM was directly initialized with the expected consensus motif. This indicates that the enrichment did not work equally well for all the RBPs studied with the Bind’n Seq method or that our method does not identify well motifs that are very short (nts, observed in the SKA enrichment analysis). In this analysis, kmer enrichments are computed by counting the number of occurrences of every possible kmer in the foreground samples (RBP concentration ) and in the background samples (RBP concentration ), and finally normalizing the foreground abundances by the background to extract the respective enrichment. The higher the enrichment of a given kmer, the higher the likelihood of it being bound by the RBP used in the experiment is thought to be. We computed these enrichments for 6mers, as done in the ENCODE studies. The results, shown in Figure 16 indicate that only RBFOX2 has a very clear hierarchy of top enriched 6mers, while the other investigated RBPs show a much flatter hierarchy of motif enrichments. An analysis of the Levenshtein distance of these motifs showed no clear difference in the pattern of distances among the leading motifs across the investigated RBPs. This suggests that these motifs correspond to many local minima of comparable depth, which precludes our algorithm finding clear PWMs representing the binding sites. Conversely, it becomes unclear whether the specificity of these RBPs would be well represented as weight matrices, or whether another model, for e.g. clusters of short, degenerate motifs may better represent the specificity of these RBPs.
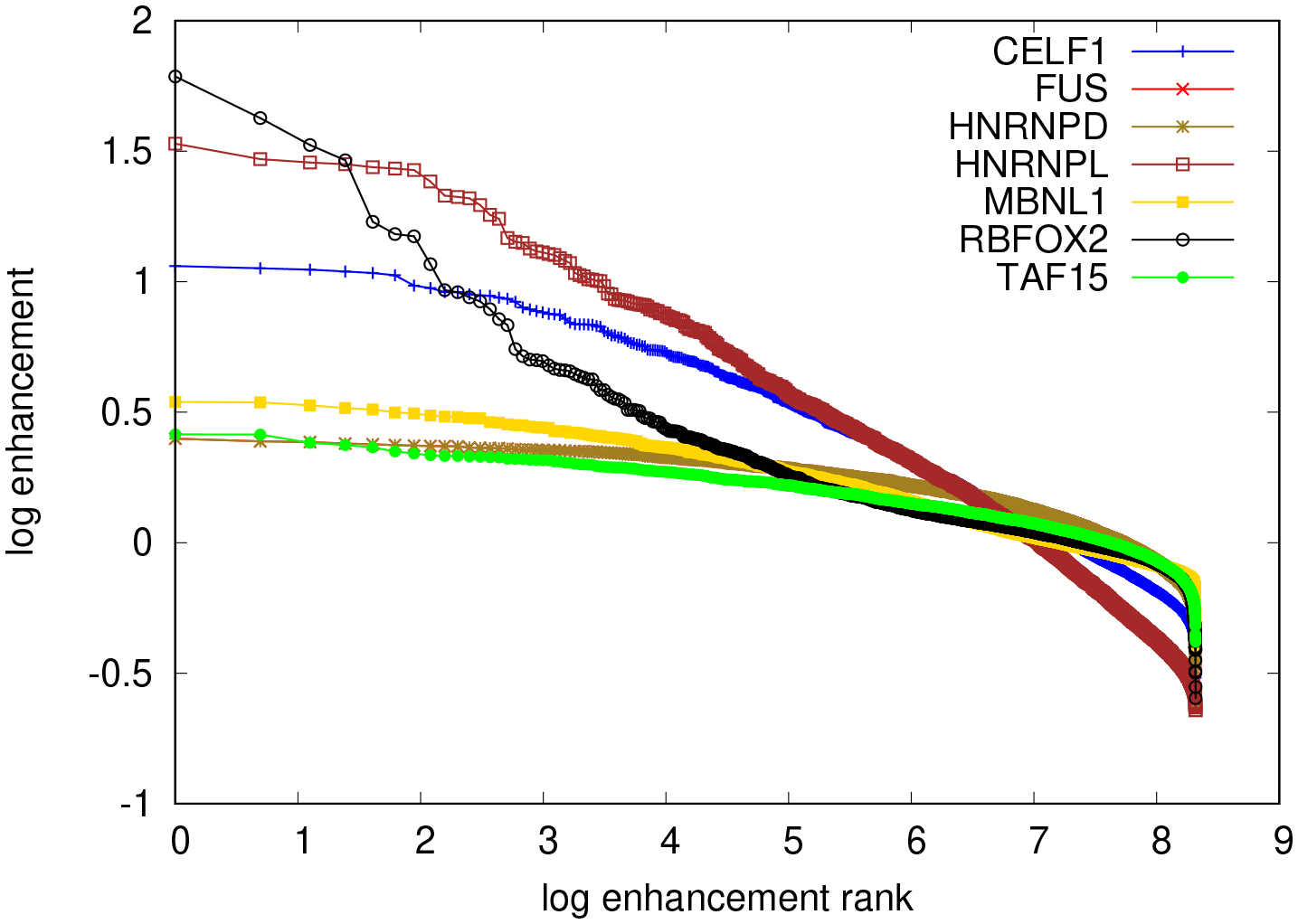
The top most enriched motifs are for RBFOX2: TGCATG, FUS: GCGCGC, hnRNPL: CACACA, MBNL1: GCTGCT, TAF15: GGGGGG. All except the RBFOX2 motif are repeats of shorter oligomers.
We constructed a thermodynamic model that can be used to infer characteristic position weight matrices for the binding domains of RBPs from data obtained from affinity-based enrichment of oligonucleotides. Since we directly model the RBP-binding specificity as PWMs, our method bypasses arbitrary choices in the alignment of kmers found to be individually enriched in the data. We evaluate our model on 111 RNA Bind’n Seq data sets in the public domain,10 finding convergent and specific motifs for 82 RBPs. For 48 of these there is complete agreement with previously reported motifs, 14 partly agree, 19 disagree, and one did not have a reported motif (PTBP3). In most cases of disagreement, our model predicts the binding element to be, in fact, poly(A), while in two cases (CPEB1 and EIF4H), we predict more complex motifs than previously reported.
Many of the RBPs for which we did not recover a PWM tend to be more degenerate motif than RBPs for which some motif emerged. E.g. ESRP1, EWSR1, FUS and other proteins have been shown to bind G-repeats, which are relatively rare in the Bind’n Seq libraries. It is likely that to identify such motifs it is crucially important that the background model is accurate. How to best construct this model remains to be determined in future work. In addition, it is possible that the binding sites of these proteins are not contiguous, linear motifs, but rather contain variable length spacers of form structures such as G-quadruplexes. It will thus be important to explore other types of models in the future, e.g. models that allow more flexible spacing of RBP contact points on RNAs in the future.
DOI’s are doi:10.17989/ experiment identifier .
Source code available from: https://git.scicore.unibas.ch/zavolan_group/pipelines/bind-n-seq-pwms 15
Archived source code and results of runs at time of publication of version 2: https://doi.org/10.5281/zenodo.11072860 48
License: MIT
We would like to thank Erik van Nimwegen for useful conversations and fruitful suggestions. Calculations were performed at sciCORE (http://scicore.unibas.ch/) scientific computing core facility at University of Basel.
| Views | Downloads | |
|---|---|---|
| F1000Research | - | - |
|
PubMed Central
Data from PMC are received and updated monthly.
|
- | - |
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: RNA-binding protein, structural biology.
Is the rationale for developing the new method (or application) clearly explained?
Yes
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
Partly
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Structural biochemistry/biophysics of multi-domain RNA-binding proteins and their target RNAs centered around solution methods NMR and SAXS
Is the rationale for developing the new method (or application) clearly explained?
No
Is the description of the method technically sound?
No
Are sufficient details provided to allow replication of the method development and its use by others?
No
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
No
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
No
References
1. Berg OG, von Hippel PH: Selection of DNA binding sites by regulatory proteins. Statistical-mechanical theory and application to operators and promoters.J Mol Biol. 1987; 193 (4): 723-50 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Theoretical Physics, Computational biology, Bioinformatics, Applied Mathematics, Algorithm
References
1. Jolma A, Zhang J, Mondragón E, Morgunova E, et al.: Binding specificities of human RNA-binding proteins toward structured and linear RNA sequences.Genome Res. 2020; 30 (7): 962-973 PubMed Abstract | Publisher Full TextCompeting Interests: No competing interests were disclosed.
Reviewer Expertise: Biophysics, statistical modeling
Is the rationale for developing the new method (or application) clearly explained?
Partly
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
No
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
No source data required
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
Partly
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: RNA-binding protein, structural biology.
Is the rationale for developing the new method (or application) clearly explained?
Yes
Is the description of the method technically sound?
Yes
Are sufficient details provided to allow replication of the method development and its use by others?
No
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?
Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?
No
Competing Interests: No competing interests were disclosed.
Reviewer Expertise: Biophysics, statistical modeling
Alongside their report, reviewers assign a status to the article:
| Invited Reviewers | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
|
Version 2 (revision) 29 May 24 |
read | read | read | read |
|
Version 1 26 Jun 23 |
read | read | ||
Provide sufficient details of any financial or non-financial competing interests to enable users to assess whether your comments might lead a reasonable person to question your impartiality. Consider the following examples, but note that this is not an exhaustive list:
Sign up for content alerts and receive a weekly or monthly email with all newly published articles
Already registered? Sign in
The email address should be the one you originally registered with F1000.
You registered with F1000 via Google, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Google account password, please click here.
You registered with F1000 via Facebook, so we cannot reset your password.
To sign in, please click here.
If you still need help with your Facebook account password, please click here.
If your email address is registered with us, we will email you instructions to reset your password.
If you think you should have received this email but it has not arrived, please check your spam filters and/or contact for further assistance.
Comments on this article Comments (0)