Spatial mapping of single cells in the <i>Drosophila</i> embryo from transcriptomic data based on topological consistency

Maryam Zand; Jianhua Ruan

doi:10.12688/f1000research.24163.2

Home Browse Spatial mapping of single cells in the Drosophila embryo from transcriptomic...

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Method Article

Revised

Spatial mapping of single cells in the Drosophila embryo from transcriptomic data based on topological consistency

[version 2; peer review: 2 approved]

Maryam Zand¹, Jianhua Ruan¹

PUBLISHED 09 Feb 2021

Author details Author details

¹ Computer science, University of Texas at San Antonio, San Antonio, Texas, 78249, USA

Maryam Zand
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Jianhua Ruan
Roles: Conceptualization, Formal Analysis, Funding Acquisition, Methodology, Project Administration, Resources, Supervision, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Bioinformatics gateway.

This article is included in the Cell & Molecular Biology gateway.

This article is included in the Single-Cell RNA-Sequencing collection.

Abstract

The advancement in single-cell RNA sequencing technologies allow us to obtain transcriptome at single cell resolution. However, the original spatial context of cells, a crucial knowledge for understanding cellular and tissue-level functions, is often lost during sequencing. To address this issue, the DREAM Single Cell Transcriptomics Challenge launched a community-wide effort to seek computational solutions for spatial mapping of single cells in tissues using single-cell RNAseq (scRNA-seq) data and a reference atlas obtained from in situ hybridization data. As a top-performing team in this competition, we approach this problem in three steps. The first step involves identifying a set of most informative genes based on the consistency between gene expression similarity and cell proximity. For this step, we propose two different approaches, i.e., an unsupervised approach that does not utilize the gold standard location of the cells provided by the challenge organizers, and a supervised approach that relies on the gold standard locations. In the second step, a Particle Swarm Optimization algorithm is used to optimize the weights of different genes in order to maximize matches between the predicted locations and the gold standard locations. Finally, the information embedded in the cell topology is used to improve the predicted cell-location scores by weighted averaging of scores from neighboring locations. Evaluation results based on DREAM scores show that our method accurately predicts the location of single cells, and the predictions lead to successful recovery of the spatial expression patterns for most of landmark genes. In addition, investigating the selected genes demonstrates that most predictive genes are cluster specific, and stable across our supervised and unsupervised gene selection frameworks. Overall, the promising results obtained by our methods in DREAM challenge demonstrated that topological consistency is a useful concept in identifying marker genes and constructing predictive models for spatial mapping of single cells.

Keywords

Single cell RNA-seq, spatial mapping, feature selection, particle swarm intelligence, nearest neighbor

Corresponding author: Jianhua Ruan

Competing interests: No competing interests were disclosed.

Grant information: This research was funded by National Science Foundation [1565076] and National Institutes of Health [U54CA217297].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Copyright: © 2021 Zand M and Ruan J. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Zand M and Ruan J. Spatial mapping of single cells in the Drosophila embryo from transcriptomic data based on topological consistency [version 2; peer review: 2 approved]. F1000Research 2021, 9:1014 (https://doi.org/10.12688/f1000research.24163.2) First published: 20 Aug 2020, 9:1014 (https://doi.org/10.12688/f1000research.24163.1) Latest published: 09 Feb 2021, 9:1014 (https://doi.org/10.12688/f1000research.24163.2)

Revised Amendments from Version 1

The current revised manuscript addresses the interesting comments raised by the reviewers. The main adjustments were clarification of the Method section and slight elaboration on Result section. More specifically, we have provided some insights and reasoning behind the selection of hyperparameter values used in our work. In addition, we provided some details about the different components of our method and our strategy to combine them for different subchallenges. The metrics used to rank different methods is now explained in the section “Evaluation metrics”. We have also added “Gold standard cell locations” subsection to explain the prediction offered by DistMap. In the result section, we have further explained the results presented in Table1 to make it clearer. Finally, we have included the running time of PSO algorithm.

See the authors' detailed response to the review by Adi Tarca
See the authors' detailed response to the review by Tianci Song and Rui Kuang

Introduction

Single cell RNA sequencing (scRNA-seq) is a cost-efficient, high throughput technology that has dramatically enhanced our understanding of developmental biology such as cell type identification, regulatory network inference, and cell trajectories^1–8. Despite many breakthroughs in biological sciences made possible by this technology, it yet suffers from the drawback that native cell location in e.g. embryo or complex tissue is often lost, except for in a few experimental methodologies which are either expensive, require highly specialized tools, or are not as widely applicable as standard scRNA-seq protocols^9–12. Given the substantial benefit offered through cell location recovery, such as obtaining a basic understanding of tissue function and disease pathology^13,14, the cell spatial reconstruction was specifically addressed in recent Single Cell Transcriptome DREAM challenge as a community-wide effort.

Many promising computational approaches dealing with the spatial reconstitution problem are centered around the main idea that an in situ atlas of a set of landmark gene’s expressions is used as a guideline to be combined with scRNA-seq profiles of individually measured cell^15,16. For instance, Seurat¹⁵ first imputes the noisy scRNAseq data then predicts the cell locations by comparing the scRNAseq gene expression pattern to its binary expression level measured by in situ data. This step is done through a mixture model. Finally, original cell location is retrieved by evaluating a posterior probability function constructed for cell-bin pairs. DistMap¹⁶ was a successful method for spatial reconstruction (of Drosophila embryo) with near single cell resolution, much higher compared to that of Seurat (3039 bins versus 128 bins). It predicts top candidate positions for a given cell by calculating the Mathews Correlation Coefficients (MCC) of binarized landmark gene expressions for every cell-bin combination. While DistMap was to some extent successful in dealing with the cell spatial mapping problem, it was limited to binarized data rather than continuous, utilized simplistic MCC analysis, and more importantly it treats each single cell independently whereas it might be more beneficial to account for collective interrelationships between cells. To more extensively explore the space of better predictive strategies, DREAM challenge aimed to exploit the atlas provided by DistMap with the hope of resolving spatial reconstruction by using incrementally fewer landmark genes (i.e. 60,40,20). Achieving this goal will help with eliminating the need for a priori reference atlas, which is expensive and time-consuming to obtain, in the future transcriptomic studies.

In this work, we proposed a top-performing method (evaluated based on three distinct scoring criteria defined by DREAM challenge) which allows us to predict the cell location consistently as accurate as DistMap while requiring fewer number of landmark genes. The details of our method and evaluation metrics are provided later in the text.

Methods

Overview of the proposed method

The general overview of our method is such that in the first step we investigate both supervised and unsupervised feature selection methods by defining two biologically rational metrics optimizing the consistency between gene expression similarity and cell proximity. In the unsupervised version we do not use the predicted cell locations given in 16 to obtain the set of most informative genes (e.g. 60,40,20), thus avoiding overfitting. On the other hand, the supervised version uses the cell locations given by DistMap as a reference. In the next, to predict the final cell locations, we use a PSO algorithm to assign proper weights to genes based on fitness functions defined by gene expression patterns. This reflects the intuition that different landmark genes are expected to demonstrate different potential in guiding us toward the proper embryo reconstruction. Finally, we use the information embedded in the cell topology to adjust the associated cell-location score with the hope to improve the predictions.

Datasets and pre-processing steps

To reconstruct Drosophila embryo from single cells, we need reference dataset (in situ), spatial coordinates, and scRNA-seq data, the details of which along with the preprosseing steps are given in the following.

Reference database The reference database (denoted as W) provides the in situ expression values as a W_3039×84 matrix where rows and columns correspond to bin locations and marker genes, respectively. The original data comes from Berkeley Drosophila Transcription Network Project (BDTNP) and in here we used the binarized format as explained in 16.

Spatial coordinates The spatial coordinate information from one half of Drosophila embryo (denoted as L) is an L_3039×3 matrix where the columns are x, y, and z coordinates of 3039 rows of bins.

Single cell RNA sequencing The scRNA-seq data (denoted as Y) gives the gene expression values as a Y_1297×8924 matrix where rows and columns are single cells and genes, respectively. In here we followed the normalization process as implemented by 16. Briefly, the raw data was first normalized with respect to the total number of unique molecular identifiers (UMI) for each cell, followed by a pseudo count addition and a log transformation. The binarization process was implemented such that the quantile was varied in order to obtain the minimum mean squared root error between the gene correlation matrix of binarized atlas and binarized scRNA-seq.

Gold standard cell locations: For each of the 1297 cells, the Mathews Correlation Coefficients (MCC) is calculated at each of the 3039 location bins between the binarized 84 RNAseq expression values for the 84 driver genes and the binarized in situ expression values for the same 84 genes. The location bin with the maximum value of MCC score is defined as the gold standard location for each cell.

Finding most informative genes

In this study, our first goal is to identify a subset of genes whose expression patterns are predictive of cell locations. We have proposed two different feature selection methods (supervised and unsupervised) to select informative genes. In the supervised method, our metric was defined based on true cell locations (gold standard). To prevent overfitting we applied a 10 fold cross validation. On the other hand, we designed an unsupervised method based on the intuition that the current locations obtained by matching the normalized and binarized scRNA-seq expression patterns with the in situ expression patterns are not necessarily the true locations of these cells. These two methods are discussed in detail in the following sections.

Unsupervised gene selection

As we believe the current locations obtained by matching the normalized and binarized scRNA-seq expression patterns with the in situ expression patterns are not necessarily the true locations of these cells, we decided to take an unsupervised feature selection approach, which does not depend on the current locations of the cells to be predicted, and therefore avoid overfitting.

The key rationale in our unsupervised feature selection method is that if a set of genes can be used as predictors of cell locations, then the cells showing similar expression patterns of these genes must be geometrically close to each other. Therefore, we defined two complementary metrics to quantitatively measure the proximity of cells with similar expression patterns for different gene subsets, and developed a greedy algorithm to search for a gene subset with the optimal (minimal) score combining the two metrics.

Metrics to measure the power of gene signatures as location predictors. The first metric relies solely on the in situ gene expression patterns in the 3039 location bins, and is calculated as follows: given a set of genes G as features, the pairwise Pearson Correlation Coefficient (PCC) is computed between the in situ expression data for every pair of the 3039 location bins; the top-10 locations with the highest PCC is then identified for each location bin; the metric $M_{1}^{G}$ is defined as the average Euclidean distance between each location bin and its top-10 most similar location bins:

M_{1}^{G} = \frac{\sum_{i = 1}^{n} \sum_{j \in L_{k i}^{G}} D_{i j}}{k \times n}, (1)

where

L_{ki}^{G}

is the set of k most similar bins for location i based on the in situ expression pattern of a gene signature G, k is fixed at 10 in this work, and n =3039 is the total number of location bins. D_ij is the Euclidean distance between the geometric coordinates of location i and location j. In this work, k is set to 10 because the evaluation of the prediction results is based on 10 best locations for each single cell. Also, based on the number of location bins (n), we believe 10 is a reasonable choice for the number of nearest neighbors.

The second metric uses information from both the in situ expression data and the scRNA-seq expression data, and is calculated as follows. Given a set of genes G as features, the pairwise PCC is computed between the scRNA-seq expression pattern of each of the 1297 cells and the in situ expression pattern of each of the 3039 location bins; then for each of the 1297 cells, the top-10 location bins with the highest PCC is identified; the metric $M_{2}^{G}$ is defined as the average Euclidean distance between the geometric coordinates of the location bin most similar to cell c and the geometric coordinates of the top-10 most similar location bins (including the most similar location):

M_{2}^{G} = \frac{\sum_{c = 1}^{m} \sum_{j \in S_{k c}^{G}} D_{l_{c}^{G} j}}{k \times m}, (2)

where

S_{kc}^{G}

is the set of top-k locations whose in situ expression patterns are most similar to the scRNA-seq expression pattern of cell c based on gene signature G, k is fixed at 10 in this work, and m =1297 is the total number of cells whose locations are to be predicted.

l_{c}^{G}

is the location bin where the expression pattern of gene signature G is most similar to cell c.

Note that the currently known most possible location of each cell c, $l_{c}^{*}$ which is predicted using all 84 genes with uniform weights, are not used in either M₁ and M₂; therefore, the gene selection process is not biased towards identifying genes to match the original locations predicted by the 84 genes. Rather, the metric provides an intrinsic measurement of the power of any subset of genes as location predictors, independent of the locations predicted with the 84 genes. In fact, the quality of the 84 genes as predictors can also be measured using these two metrics, and compared to any other gene sets; it is possible that a subset of the 84 genes can receive higher scores in these two metrics than the original 84 genes. In contrast, using a supervised feature selection method, where the “true” location is defined using all 84 genes, any subset of genes will be necessarily inferior to the complete set of 84 genes.

Step-wise backward elimination feature selection algorithm. We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of $M_{1}^{G} and M_{2}^{G}$ . Briefly, starting with a set of q genes, we computed $M_{1}^{G} and M_{2}^{G}$ for all possible subsets of q − 1 genes by removing one gene at a time from the set. The subset with the minimal $M_{1}^{G} + M_{2}^{G}$ is then recorded as the best subset of size q − 1. This procedure is then repeated until a desired number of genes is reached. As this algorithm is a greedy approach, it does not guarantee to find the optimal solution. We have also attempted to combine backward elimination with forward selection, which only improved the solution slightly. Due to the excessive running time required, we opted to use the simple algorithm described above while leaving additional improvement as future work.

Supervised gene selection

While in the unsupervised approach metrics M1 and M2 were optimized, in the supervised version a single metric N was defined as explained below. This metric, which relies on both the scRNA-seq gene expression patterns in the 1297 cells and the gold standard location of each cell, is calculated as follows: given a set of genes G as features, the pairwise PCC is computed between the scRNA-seq expression data for every pair of the 1297 cells; the top-10 cells with the highest PCC is then identified for each cell; the metric N^G is defined as the average Euclidean distance between the gold standard geometric coordinates of each cell and its top-10 most similar cells:

N^{G} = \frac{\sum_{c = 1}^{m} \sum_{j \in T_{k c}^{G}} D_{l_{c}^{*} l_{j}^{*}}}{k \times m}, (3)

where

T_{kc}^{G}

is the set of top-k cells whose scRNA-seq expression patterns are most similar to the scRNA-seq expression pattern of cell c based on gene signature G, k is fixed at 10 in this work, and m =1297 is the total number of cells whose locations are to be predicted.

l_{c}^{*}

is the “gold standard” cell location for cell c, which is predicted using all 84 genes.

Supervised learning to find optimal gene weights

It is intuitive to assume that the contribution of genes in determining cell locations are not equal. Therefore, we look for a way to learn how to assign proper weight to each selected gene for more accurate prediction of cell locations. To this end, we chose a supervised learning approach, using the cell locations predicted by the highest MCCs with the 84 signature genes as “gold standard” locations. To avoid overfitting, we performed 10-fold cross-validation: gene weights were determined using the scRNA-seq data of 90% of cells; these weights are then used to predict the locations of the remaining 10% of the cells not used in training. The splitting of the data is saved, for reproducibility of the results.

The basic idea of the PSO algorithm is as follows. We created a set of agents, each of which is initiated with a gene weight vector w_i of size |G|× 1. Each weight vector is evaluated by how closely the weighted gene expression pattern can be used to predict the cell locations when compared to the “gold standard” locations obtained with the 84 genes:

M_{3}^{w, G} = \frac{\sum_{c = 1}^{m} \sum_{j \in S_{k c}^{w, G}} D_{l_{c}^{*} j}}{k \times m}, (4)

where

S_{k c}^{w, G}

is the set of top-k location bins whose in situ expression patterns are most similar to the weighted expression pattern of cell c based on a given gene signature set G. The similarity is measured by PCC here. k is fixed at 10, and m is the total number of cells in the training set.

l_{c}^{*}

is the “gold standard” cell location for cell c, which is predicted using all 84 genes with uniform weights.

During the search, each agent keeps track of a personal best weight vector P best_i, and the global best solution from all agents is denoted Gbest. At each iteration, the weight vector of each agent is updated by the differences between the current weight and the personal best and global best weight vectors:

w_{i} = w_{i} + α \times r_{1} \circ (P b e s t_{i} - w_{i}) + β \times r_{2} \circ (G b e s t - w_{i}),

where α and β are constants to control the granularity of the search and speed of convergence. We choose α = β = 0.2 with 200 agents and the maximum number of iterations is 40. The operator ∘ denotes entry-wise vector multiplication. r₁ and r₂ are vectors of random numbers uniformly distributed between 0 and 1, generated independently for each agent at each iteration. α and β are acceleration coefficients, also referred to as trust parameters. α expresses how much confidence a particle has in itself, while β expresses how much confidence a particle has in its neighboring particles. Particles draw their strength from their cooperative nature and are most effective when α and β coexist in a good balance. Most applications use α=β. Low values for α and β result in smooth particle trajectories, while high values cause more acceleration, with abrupt movement towards or past good regions. In this study we used α=β=0.2, with 200 agents and the maximum number of iterations set to 40. These parameters were manually tuned by observing the values of the fitness function to reach desired search granularity and speed of convergence. The running time of PSO algorithm is about 15 hours when running on a system with 16 GB of memory. However, the running time could depend on different optimization settings such as parameter α and β.

Neighbor-weighted cell location prediction

The location prediction for each single cell relies on the (weighted) similarity between the expression pattern of selected signature genes in the cell and every location bin. It is important to note that the expression patterns in neighboring cells should be similar in general, and therefore the overall prediction should take the expression of nearby location bins into consideration. Intuitively, if the globally highest scoring location is far away from locations with slightly lower but comparable scores, the confidence score for the highest-scoring location should be reduced; on the other hand, a locally highest-scoring location close to other high-scoring locations should be upweighted. Therefore, to make the final prediction for a given cell, we adjusted the prediction score based on the prediction scores from neighbor locations.

Formally, let C = (c_ij)_n×m be the bin-cell association matrix, where c_ij is the PCC between the (weighted) scRNA-seq data and the in situ hybridization data for every pair of cells and locations. n = 3039 is the number of candidate location bins, and m is the number of cells in the test set, Let D = (d_ij)_n×n be the Euclidean distance matrix between the geometric coordinates of every pair of location bins. We define an affinity matrix A = (a_ij)_n×n such that $a_{i j} = e^{- \frac{d_{i j}}{d *}}$ , where d* is a parameter to control how many neighbor locations can impact the final prediction score. A smaller d* value means fewer neighbor locations to be considered. To have a robust measure of how geometrically close two location bins can be, we first measure the distance between each location and its nearest location, and then computed the median of these shortest distances as d*. As a result, most a_ijs’ are much smaller than e⁻¹, and only a limited number of neighbor locations with very high scores can impact the final prediction score for each cell.

The final prediction score matrix P = (p_ij)_n×m is calculated by P = A × C. Since a_ii = 1 and a_ij ≤ 1 for all j ≠ i, it is easy to see that

P_{i j} = \sum_{k = 1}^{n} a_{i k} c_{k j} = c_{i j} + \sum_{k \neq j} a_{i k} c_{k j} \cdot

Therefore, the final prediction score for a cell i to be at a particular location j is the weighted sum of the similarity scores between the expression pattern of cell i and all locations, where the weight is an exponentially decreasing function of the geometric distance from location j.

From the final predicted bin-cell association matrix, we reported the 10 locations with the highest scores for each cell as the most likely positions in embryo.

How proposed method applied to different subchallenges

During the challenge period, each team was given a limited number of attempts to test the success of their proposed approach(es) - evaluation results and ranking for all teams were shown in a leaderboard, with no details of the evaluation metrics. It was made clear that different methods could be used for different sub-challenges. Our final results for subchallenge 1 were obtained with both PSO and neighbor weighting. For subchallenge 2, we were not able to perform PSO due to a lack of time. On the other hand, it was also our observation that PSO only resulted in modest improvement with almost no impact to our ranking based on feedback from previous rounds. Therefore, the 40 genes obtained from gene selection in subchallenge 2 were utilized with uniform weights. In subchallenge 3, genes were weighted with the PSO procedure, but we did not perform neighbor weighting. The rationale is that, as subchallenge 3 used substantially fewer genes, the quality of the location prediction may be relatively low and therefore using gene expression information from the predicted neighbors may actually degrade the final prediction.

Post-challenge phase

In this phase to evaluate the robustness and soundness of the method, a 10 fold CV scenario was performed to obtain 10 different sets of informative genes using a subset of cells. To compare the similarity of the selected genes, Jaccard similarity was defined as follows:

J (A, B) = \frac{| A \cap B |}{| A \cup B |} (5)

where A and B are two sets of informative genes and J(A, B) measures the ratio of the number of common genes and the total number of genes presented in two sets. In addition, the expected Jaccard similarity was computed as follows:

E (J) = \sum_{k = 0}^{m} \frac{k}{2 m - k} \frac{(\begin{matrix} m \\ k \end{matrix}) (\begin{matrix} n − m \\ m − k \end{matrix})}{(\begin{matrix} n \\ m \end{matrix})} (6)

where, n is the total number of genes, here 84, and m is the number of genes in our selected gene set, 60,40, and 20 for subchallenge 1,2, and 3, respectively.

DREAM consortium evaluation metrics

Our method was designated as a top-performing method among 34 participating teams. To evaluate and rank the teams, the challenge organizers had defined three scoring metrics s1, s2, and s3, which were not disclosed to participants at the time of submission. The details of each metric are available in 17 and are quite complex. Here, we briefly explain each scoring metric and the general intuition behind them.

The first metric s₁ computes the weighted average of the Mathew Correlation Coefficient (MCC) between the in situ profile of the ground truth cell location (as predicted by DistMap) and the in situ profile of the most probable prediction location for that cell¹⁷.

s_{1} = \sum_{c = 1}^{N} \frac{p_{K} (c, A)}{\sum_{i = 1}^{N} p_{K} (i, A)} M C C (f_{A (c, 1, K)}, f_{𝜖_{c}})

where N is the total number of cells with predicted locations, A(c, i, K) represents the predicted i−th most probable location for cell c using K genes, 𝜖_c the ground truth location bin for cell c, and f_{𝜖_c} the in situ expression profile at 𝜖_c for the K selected genes. The weights are calculated as $p_{k} (c, A) = \frac{d_{84} (c, A)}{d_{k} (c, A)},$ where d_k(c,A) is the average euclidean distance between the geometric coordinates of the ground truth location of cell c and the top-10 locations predicted using k genes. d₈₄(c,A) is the value of d_k(c,A) using k = 84.

The second metric, s₂ only considers how the averaged location prediction of the 10 most probable predictions using 60, 40, and 20 genes is compared to that of the one predicted by using all the 84 genes¹⁷. As is evident, this metric does not include either of the accuracy of the in situ expression profile prediction and the closeness of in situ and scRNA-seq data.

s_{2} = \frac{1}{N} \sum_{c = 1}^{N} p_{k} (c, A)

Finally, s₃ accounts for how the scRNA-seq expression of 60,40, and 20 genes of the best predicated locations is closely approximating that of the in situ expression patterns¹⁷.

s_{3} = \sum_{s = 1}^{K} \frac{M C C (t_{c s}, f_{𝜖_{c} s}) \forall c}{\sum_{i = 1}^{K} M C C (t_{c i}, f_{𝜖_{i} r}) \forall c} M C C (t_{c s}, f_{A (c, 1, K) s}) \forall c

where t_cs represents the binarized expression value of gene s in cell c, and ∀c denotes that MCC is calculated cell wise for each gene.

Software

The method proposed here is written in Matlab 2018b and the source code is available from GitHub¹⁸

It does not utilize or rely on any specific Matlab toolbox. Therefore by following the clear detailed formulation provided in manuscript this method can readily be implemented in any open-access software.

Results and discussion

Performance evaluation

Table 1 shows the results of our supervised and unsupervised methods on the three subchallenges, evaluated by the three metrics (s1, s2, and s3) proposed by the DREAM challenge organizers. The details of these metrics are discussed in Method Section “DREAM consortium evaluation metrics”. A more detailed analysis of the results and comparison with other top-performing algorithms are presented in 17, and is not repeated here. To obtain some additional insights of our algorithms’ performance, we present here the results of some variations of our proposed methods. Both our supervised and unsupervised methods have two important components, (1) gene selection, and (2) neighbor-weighted cell location prediction, integral to selecting a set of most informative genes and locating cells based on the information buried in cell neighborhood network topology. To understand the importance of these two components, we designed a set of baseline studies incorporating four experiments. In these experiments, the gene selection strategy was replaced by either selecting genes randomly, or selecting genes expressed in the most number of cells (high degree genes). The neighbor-based reweighting component was also removed in two of these experiments.

The subchallenge scores corresponding to our method (supervised and unsupervised) along with these four baseline studies are listed in Table 1 under the group A and group B, respectively. The method with highest score (s1, s2, s3) in each of the three subchallenges is shown in boldface. It can be seen that the supervised and unsupervised methods (group A) achieved comparable results, and significantly outperformed the baseline approaches (group B) on average, for all three subchallenges. For subchallenge 3, which is the most difficult task, both of our methods significantly outperformed the baseline approaches in all three metrics. On the other hand, for subchallenge 1, for which the goal is to select 60 genes to best approximate the cell locations determined by 84 genes, random gene selection coupled with neighbor-based reweighting achieved almost the same performance as our unsupervised approach, and is only slightly inferior to the supervised approach. This is understandable because of the extensive overlap between the randomly selected genes and the “optimal” gene set. High degree selection achieved somewhat less accurate results than random selection, indicating that some less frequently expressed genes are important determinants of cell locations. For subchallenge 2, our proposed methods outperformed all four baseline approaches in s2, and three out of the four baseline approaches in s1 and s3. Finally, comparing the four baseline approaches suggest that the neighbor-based reweighting component significantly improved s2, but its impacts on the other two metrics are somewhat mixed. Overall, the significant performance gain in subchallenge 3 compared to random gene selection and high degree gene selection supports that the small set of genes we identified are important for predicting cell locations.

Table 1. Numerical values of subchallenges scores are given for the ease of comparison with some designed baseline methods.

	SubCh1			SubCh2			SubCh3
gene selection method	s1	s2	s3	s1	s2	s3	s1	s2	s3
Group A
Our Unsupervised method	0.6610	1.4522	0.6122	0.6552	1.3176	0.6538	0.6620	1.0166	0.7928
Our Supervised method	0.6730	1.5463	0.5937	0.6558	1.3719	0.6731	0.6534	1.0994	0.7807
Group B
Random gene selection	0.6736	1.0638	0.6289	0.6113	0.6930	0.6240	0.5362	0.5052	0.7283
Random gene selection + neigh based reweighting	0.6714	1.4043	0.5762	0.6642	1.139	0.6619	0.5734	0.6997	0.6964
High degree gene selection	0.6914	0.904	0.5860	0.6061	1.0163	0.5969	0.5653	0.6156	0.7159
High degree gene selection + neigh based reweighting	0.6702	1.3241	0.5706	0.6134	1.027	0.5978	0.5593	0.7065	0.6468
Avg of all metrics in group A for each subchallenge		0.9231			0.8879			0.8342
Avg of all metrics in group B for each subchallenge		0.8137			0.7376			0.6291

The predictions mentioned above did not involve any additional pre-processing steps, e.g. imputation, on the provided input data. We simply used the binarized and normalized in situ hybridization and scRNA-seq data. However, for the sake of completeness we also examined the possible role of "imputation" and using raw data instead of the binarized scRNA-seq data. We tried to impute the dropouts in scRNA-seq data using SAVER¹⁹ and netImpute²⁰, but no significant improvement was gained in terms of enhancing our metric scores. On the other hand, although our analysis indicated that using raw data instead of the binarized data can potentially increase the consistency between gene expression pattern similarity and cell proximity in this challenge (according to M₁ and M₂ metrics), we are limited by the fact that the true locations of the cells to be predicted are unknown, and prediction accuracy is at least partially defined by comparing to the “gold standard” location obtained from binarized data. We speculate that anyone using raw data would probably be disadvantaged. It is noteworthy that our method is applicable if one prefers to use raw data instead of binarized data, and our results (data not shown; available as underlying data) indicate that there is benefit of using raw data instead of binarized data.

Robustness of marker genes

In the post-challenge phase of the competition the data set was divided into train and test subsets using 10-fold cross-validation in order to further investigate to what degree the set of most informative genes are consistent across different subset of cells selected through the 10 fold CV analysis. The results given in Figure 1 show that the Jaccard similarity between different folds are higher than the expected similarity in all three subchallenges indicating that there in fact exists a consistency in the most-informative genes selected across different folds. Moreover, as the number of genes allowed in a subchallenge decreases (from subchallenge 1 to subchallenge 3) the difference between Jaccard similarity of the most-informative genes and its expected value becomes more and more pronounced.

Figure 1. Boxplot shows the Jaccard similarity between the genes selected for each of the 10 CV scheme in all 3 subchallenges.

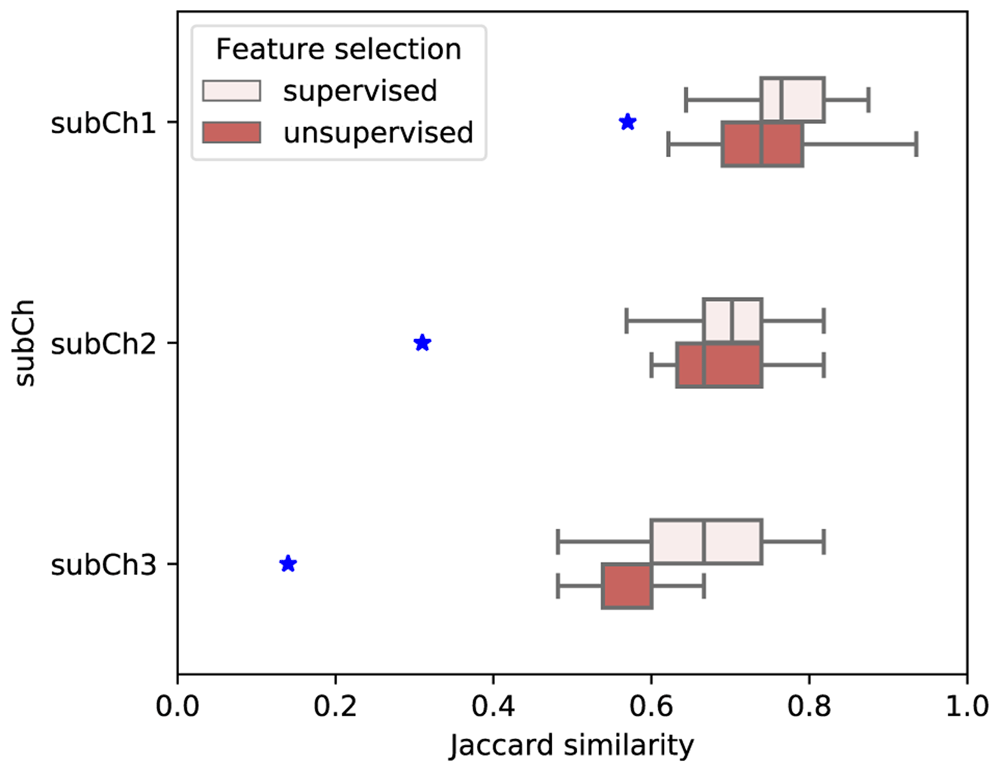
Blue stars represent expected Jaccard similarity.

Figure 2 shows the Venn diagram of 20 most informative genes selected from supervised and unsupervised methods. Out of 20 genes selected by each method, there are 11 common genes identified by both methods, which is more than expected (p-value < 0.0005, Fisher’s exact test).

Figure 2. The Venn diagram shows 20 genes selected from supervised and unsupervised methods out of which 11 genes are common for both methods.

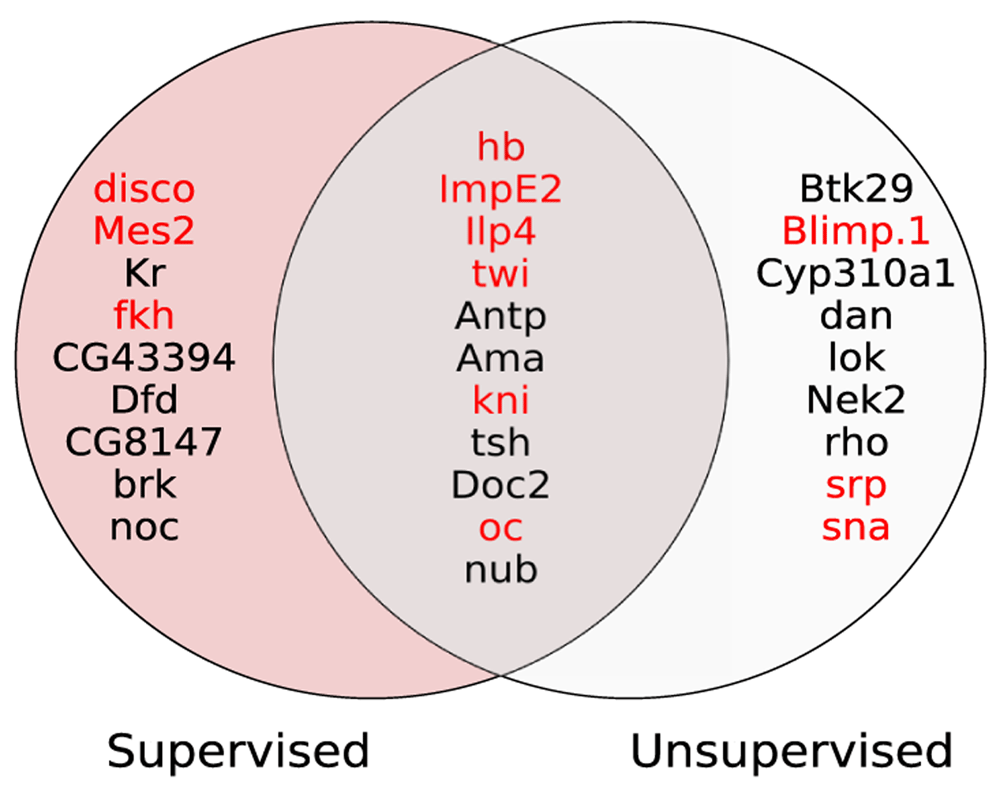
The 12 genes denoted by red color are the scRNA cluster-specific genes reported in DistMap.

Another interesting observation is that cluster-specific genes (denoted by red color) are prevalent in the set of most informative genes obtained from both supervised and unsupervised methods. This finding highlights our method was in fact able to take advantage of those 12 cluster-specific genes which contain cell location information.

Recovering gene expression pattern

To virtually reconstruct gene expression patterns, the result of our method (i.e. bin-cell association matrix) was processed based on the methodology of vISH - a tool developed in 16 to derive the expression pattern of each of the 84 genes across the location bins, and compared with the expression patterns obtained by DistMap. Figure 3 shows the distribution of the PCC between DistMap and our results from the three subchallenges. Overall, there is a high correlation among reference patterns (DistMap) and patterns generated by our method. The average correlation in the three sub-challenges are 0.81, 0.76, and 0.68, respectively. In sub-challenge 1, almost all genes have been reliably reconstructed, while for sub-challenge 3, a small number of genes have fairly low reconstruction rate.

Figure 3. Histogram of correlation between gene patterns predicted by our method and DistMap using 60,40,20 genes.

Figure 4 shows the reconstructed expression patterns for three genes: twi, cad, and ftz, which play key roles in the regulatory network of early Drosophila development. Overall, there is good agreement between our predictions and that of DistMap. In case of twi, our method and DistMap both very precisely predicted the in situ expression pattern. In fact, twi is one the 20 genes selected by both the supervised and unsupervised feature selection methods, due to its distinct expression patterns associated with cell spatial arrangement in the embryo. For cad, DistMap and our method with as few as 20 genes predicted very similar expression patterns, where there is a higher expression in the posterior domain, consistent with the current knowledge of cad in embryo development²¹. On the other hand, the predicted expression patterns seem to be much more diffused than the in situ expression pattern, potentially because of the binarization of the in situ data, which caused loss of weaker signals. Finally, for ftz, while the predicted expression pattern by our method with 60 genes is in general agreement with DistMap and in situ data, our method with 40 or 20 genes failed to reconstruct the expression pattern of ftz associated with the segmentation of Drosophila embryos²². While it is possible that more refined parameters such as a smaller number of neighbor cells may improve the prediction of our method, we believe the striped pattern of ftz makes it difficult, if not impossible, for any method that aims at a much reduced number of marker genes for spatial mapping.

Figure 4. Expression pattern of three sample genes are given for in situ, DistMap, and our method using 60,40,20 genes.

Conclusion

In this work, we proposed a method to identify gene markers for RNAseq-based reconstruction of cell spatial information that were lost during single-cell transcriptomics sequencing of Drosophila embryo. The main hypothesis of this study is that the topology of the marker gene expression based cell-cell similarity graph should be consistent with the topology of the cell-cell geometric location map. To test the hypothesis, several metrics were defined based on this biological rationale to capture the consistency between gene expression similarity and cell proximity. A greedy step-wise backward elimination feature selection algorithm was implemented to find a set of most informative genes to optimize these metrics. Next, a Particle Swarm Optimization algorithm was developed to obtain optimal gene weights to construct the cell-location association matrix. Finally, the prediction score of a cell’s location was further improved by considering the expression similarity between neighboring locations. It was shown that our method can successfully identify markers genes capable of predicting cell locations with high accuracy. In addition, it was also demonstrated that our method can recover the spatial expression patterns of most embryo marker genes. Even though the method proposed here was custom designed for this Drosophila embryo problem, it has the potential to be readily applied to other organisms as well.

Data availability

Underlying data

The challenge datasets can be accessed at https://www.synapse.org/#!Synapse:syn16782375

Challenge documentation, including the detailed description of the Challenge design, overall results, scoring scripts, and the clinical trials data dictionary can be found at: https://www.synapse.org/#!Synapse:syn15665609/wiki/582909

Software availability

Source code is available from: https://github.com/mary77/scSpatialMapping.git

Archived source code at time of publication: https://doi.org/10.5281/zenodo.3877577¹⁸

License: MIT

Faculty Opinions recommended

References

1. Kolodziejczyk AA, Kim JK, Svensson V, et al.: The Technology and Biology of Single-Cell RNA Sequencing. Mol Cell. 2015; 58(4): 610–620. PubMed Abstract | Publisher Full Text
2. Altschuler SJ, Wu LF: Cellular Heterogeneity: Do Differences Make a Difference? Cell. 2010; 141(4): 559–563. PubMed Abstract | Publisher Full Text | Free Full Text
3. Tang F, Barbacioru C, Wang Y, et al.: mRNA-Seq whole-transcriptome analysis of a single cell. Nat Methods. 2009; 6(5): 377–382. PubMed Abstract | Publisher Full Text
4. Wang Z, Gerstein M, Snyder M: RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet. 2009; 10(1): 57–63. PubMed Abstract | Publisher Full Text | Free Full Text
5. Meamardoost S, Bhattacharya M, Hwang EJ, et al.: FARCI: Fast and Robust Connectome Inference. bioRxiv. 2020. Publisher Full Text
6. Huang S: Non-genetic heterogeneity of cells in development: more than just noise. Development. 2009; 136(23): 3853–3862. PubMed Abstract | Publisher Full Text | Free Full Text
7. Shalek AK, Satija R, Shuga J, et al.: Single-cell RNA-seq reveals dynamic paracrine control of cellular variation. Nature. 2014; 510(7505): 363–369. PubMed Abstract | Publisher Full Text | Free Full Text
8. Wagner A, Regev A, Yosef N: Revealing the vectors of cellular identity with single-cell genomics. Nat Biotechnol. 2016; 34(11): 1145–1160. PubMed Abstract | Publisher Full Text | Free Full Text
9. Casasent AK, Schalck A, Gao R, et al.: Multiclonal Invasion in Breast Tumors Identified by Topographic Single Cell Sequencing. Cell. 2018; 172(1–2): 205–217.e12. PubMed Abstract | Publisher Full Text | Free Full Text
10. Ståhl PL, Salmén F, Vickovic S, et al.: Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science. 2016; 353(6294): 78–82. PubMed Abstract | Publisher Full Text
11. Lovatt D, Ruble BK, Lee J, et al.: Transcriptome in vivo analysis (TIVA) of spatially defined single cells in live tissue. Nat Methods. 2014; 11(2): 190–196. PubMed Abstract | Publisher Full Text | Free Full Text
12. Rodriques SG, Stickels RR, Goeva A, et al.: Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science. 2019; 363(6434): 1463–1467. PubMed Abstract | Publisher Full Text | Free Full Text
13. Oh SW, Harris JA, Ng L, et al.: A mesoscale connectome of the mouse brain. Nature. 2014; 508(7495): 207–214. PubMed Abstract | Publisher Full Text | Free Full Text
14. Hawrylycz MJ, Lein ES, Guillozet-Bongaarts AL, et al.: An anatomically comprehensive atlas of the adult human brain transcriptome. Nature. 2012; 489(7416): 391–399. PubMed Abstract | Publisher Full Text | Free Full Text
15. Satija R, Farrell JA, Gennert D, et al.: Spatial reconstruction of single-cell gene expression data. Nat Biotechnol. 2015; 33(5): 495–502. PubMed Abstract | Publisher Full Text | Free Full Text
16. Karaiskos N, Wahle P, Alles J, et al.: The Drosophila embryo at single-cell transcriptome resolution. Science. 2017; 358(6360): 194–199. PubMed Abstract | Publisher Full Text
17. Tanevski J, Nguyen T, Truong B, et al.: Gene selection for optimal prediction of cell position in tissues from single-cell transcriptomics data. Life Sci Alliance. 2020; 3(11): e202000867. PubMed Abstract | Publisher Full Text | Free Full Text
18. Zand M, Ruan J: mary77/scspatialmapping: First release of scspatialmapping. Zenodo. 2020. http://www.doi.org/10.5281/zenodo.3877577
19. Huang M, Wang J, Torre E, et al.: SAVER: gene expression recovery for single-cell RNA sequencing. Nat Methods. 2018; 15(7): 539–542. PubMed Abstract | Publisher Full Text | Free Full Text
20. Zand M, Ruan J: Network-based single-cell rna-seq data imputation enhances cell type identification. Genes (Basel). 2020; 11(4): 377. PubMed Abstract | Publisher Full Text | Free Full Text
21. Stauber M, Lemke S, Schmidt-Ott U: Expression and regulation of caudal in the lower cyclorrhaphan fly megaselia. Dev Genes Evol. 2008; 218(2): 81–87. PubMed Abstract | Publisher Full Text | Free Full Text
22. Lim B, Fukaya T, Heist T, et al.: Temporal dynamics of pair-rule stripes in living drosophila embryos. Proc Natl Acad Sci U S A. 2018; 115(33): 8376–8381. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 20 Aug 2020

Author details Author details

¹ Computer science, University of Texas at San Antonio, San Antonio, Texas, 78249, USA

Maryam Zand
Roles: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

This research was funded by National Science Foundation [1565076] and National Institutes of Health [U54CA217297].
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Article Versions (2)

version 2

Revised

Published: 09 Feb 2021, 9:1014

https://doi.org/10.12688/f1000research.24163.2

version 1

Published: 20 Aug 2020, 9:1014

https://doi.org/10.12688/f1000research.24163.1

© 2021 Zand M and Ruan J. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Zand M and Ruan J. Spatial mapping of single cells in the Drosophila embryo from transcriptomic data based on topological consistency [version 2; peer review: 2 approved]. F1000Research 2021, 9:1014 (https://doi.org/10.12688/f1000research.24163.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 09 Feb 2021

Revised

Views

Reviewer Report 23 Mar 2021

Tianci Song, Department of Computer Science and Engineering, University of Minnesota, Minneapolis, MN, USA

Rui Kuang, Department of Computer Science and Engineering, University of Minnesota, Twin Cities, Minneapolis, MN, USA

Approved

https://doi.org/10.5256/f1000research.54404.r79202

The authors have addressed all ... Continue reading

CITE

Report a concern

Respond or Comment

Views

Reviewer Report 18 Feb 2021

Adi Tarca, Department of Computer Science, College of Engineering, Wayne State University, Detroit, MI, USA

Approved

https://doi.org/10.5256/f1000research.54404.r79203

The authors have address all my concerns but one. This reviewer does not agree with the use of “unsupervised” attribute for method M2. Although this reviewer does not dispute the fact that the method was tested, and that it does not overfit the data, I still believe the method is supervised. To give you a conceptually similar example, lets’ say you want to predict the BMI of a person based on some image features. However instead of fitting your model to the actual BMI values you use a proxy for it (e.g. weight) instead. Of course your model will not perfectly recall the BMI values but this does not mean you did not use information disclosing in part the outcome you want to predict. Back to our problem, the authors may not be using the exact bin locations of the single cells (gold standard) but they are using proxies for them derived from the same or partially the same information used to establish the gold standard. Therefore, I would suggest to remove the term unsupervised when describing this method.

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Machine learning, genomics, statistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 20 Aug 2020

Views

Reviewer Report 18 Sep 2020

Adi Tarca, Department of Computer Science, College of Engineering, Wayne State University, Detroit, MI, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.26653.r69942

The authors describe their approach to the DREAM Single cell prediction challenge that was designed to find optimal subsets of 20, 40, and 60 genes that would allow prediction of single cells locations in a dme embryo with minimal accuracy loss relative to locations based on 84 genes. The method could be useful in similar applications, yet I have the following comments:

Major:

The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.
The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

Minor:

The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

Is the rationale for developing the new method (or application) clearly explained?

Partly
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Machine learning, genomics, statistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 09 Feb 2021

Maryam Zand, Computer science, University of Texas at San Antonio, San Antonio, 78249, USA

09 Feb 2021

Author Response

We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors ... Continue reading We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors describe their approach to the DREAM Single cell prediction challenge that was designed to find optimal subsets of 20, 40, and 60 genes that would allow prediction of single cells locations in a dme embryo with minimal accuracy loss relative to locations based on 84 genes. The method could be useful in similar applications, yet I have the following comments:

Major:
(Q1) The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.

(A1) Firstly, we agree that the “unsupervised” version of our method does not strictly follow the DREAM challenge rule of not using in situ data directly. The reason is that we were not aware of the rule until after our submission. (The rule was posted in the discussion forum instead of on the challenge main webpage, and there were a lot of discussions about this issue among other participants as well). This is why we were allowed to submit, “unofficially”, a supervised version after discussing with the DREAM organizers. Despite violating the DREAM challenge rule, we believe the “unsupervised” method we describe here has been evaluated rigorously and the ideas are valuable, based on both post-challenge analysis results, as well as arguments presented below.
Secondly, we argue that the M2 metric that we proposed is indeed unsupervised instead of supervised learning. In a supervised method, you optimize parameters in order to achieve the minimal deviation from ground truth (or gold standard in this work). Since the gold standard in this work is defined with all 84 genes, when you reduce the number of genes, you expect to gradually increase the gap between the gold standard and the prediction, and the goal is to minimize the gap with K genes. Our proposed metric M2 does not aim to reduce deviation from ground truth. In fact, the values of M2 achieved with the genes that we selected have better M2 values than the initial 84 genes, which potentially indicate that the initial 84 genes are not “optimal”. Another way to look at this is that we do not use the “gold standard” position in determining how good or bad the selected genes are. The definition of M2 relies on lcG , the location bin whose expression profile of gene set G is the most similar to cell c among all location bins. Although initially when G has all 84 genes, lcG is indeed identical to the gold standard, lc* , this set of locations moves away from the gold standard when the gene set changes – so you could say that we have a “moving” gold standard if you wish, and the fact is that with 20 genes, lcG is quite different from lc*. Furthermore, while we implemented a stepwise backward elimination method to choose G genes from 84 genes, we could have started with any random set of genes or the whole RNAseq dataset (with much longer running time, however). In fact, our analysis results showed that the M2 values on test data can often be better than the M2 values on training data, further supporting that this is not a supervised method.

(Q2) The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

(A2) We have included this information in the revised manuscript:
“The running time of PSO algorithm is about 15 hours when running on a system with 16 GB of memory. However, the running time could depend on different optimization settings such as parameter alpha and beta.”

Minor:
(Q3) The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

(A3) M1 and M2 were defined based on Euclidean distances and our objective was indeed to minimize M1+M2, not to maximize it.
We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors describe their approach to the DREAM Single cell prediction challenge that was designed to find optimal subsets of 20, 40, and 60 genes that would allow prediction of single cells locations in a dme embryo with minimal accuracy loss relative to locations based on 84 genes. The method could be useful in similar applications, yet I have the following comments:

Major:
(Q1) The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.

(A1) Firstly, we agree that the “unsupervised” version of our method does not strictly follow the DREAM challenge rule of not using in situ data directly. The reason is that we were not aware of the rule until after our submission. (The rule was posted in the discussion forum instead of on the challenge main webpage, and there were a lot of discussions about this issue among other participants as well). This is why we were allowed to submit, “unofficially”, a supervised version after discussing with the DREAM organizers. Despite violating the DREAM challenge rule, we believe the “unsupervised” method we describe here has been evaluated rigorously and the ideas are valuable, based on both post-challenge analysis results, as well as arguments presented below.
Secondly, we argue that the M2 metric that we proposed is indeed unsupervised instead of supervised learning. In a supervised method, you optimize parameters in order to achieve the minimal deviation from ground truth (or gold standard in this work). Since the gold standard in this work is defined with all 84 genes, when you reduce the number of genes, you expect to gradually increase the gap between the gold standard and the prediction, and the goal is to minimize the gap with K genes. Our proposed metric M2 does not aim to reduce deviation from ground truth. In fact, the values of M2 achieved with the genes that we selected have better M2 values than the initial 84 genes, which potentially indicate that the initial 84 genes are not “optimal”. Another way to look at this is that we do not use the “gold standard” position in determining how good or bad the selected genes are. The definition of M2 relies on lcG , the location bin whose expression profile of gene set G is the most similar to cell c among all location bins. Although initially when G has all 84 genes, lcG is indeed identical to the gold standard, lc* , this set of locations moves away from the gold standard when the gene set changes – so you could say that we have a “moving” gold standard if you wish, and the fact is that with 20 genes, lcG is quite different from lc*. Furthermore, while we implemented a stepwise backward elimination method to choose G genes from 84 genes, we could have started with any random set of genes or the whole RNAseq dataset (with much longer running time, however). In fact, our analysis results showed that the M2 values on test data can often be better than the M2 values on training data, further supporting that this is not a supervised method.

(Q2) The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

(A2) We have included this information in the revised manuscript:
“The running time of PSO algorithm is about 15 hours when running on a system with 16 GB of memory. However, the running time could depend on different optimization settings such as parameter alpha and beta.”

Minor:
(Q3) The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

(A3) M1 and M2 were defined based on Euclidean distances and our objective was indeed to minimize M1+M2, not to maximize it.
Competing Interests: no competing interests Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 09 Feb 2021

Maryam Zand, Computer science, University of Texas at San Antonio, San Antonio, 78249, USA

09 Feb 2021

Author Response

We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors ... Continue reading We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors describe their approach to the DREAM Single cell prediction challenge that was designed to find optimal subsets of 20, 40, and 60 genes that would allow prediction of single cells locations in a dme embryo with minimal accuracy loss relative to locations based on 84 genes. The method could be useful in similar applications, yet I have the following comments:

Major:
(Q1) The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.

(A1) Firstly, we agree that the “unsupervised” version of our method does not strictly follow the DREAM challenge rule of not using in situ data directly. The reason is that we were not aware of the rule until after our submission. (The rule was posted in the discussion forum instead of on the challenge main webpage, and there were a lot of discussions about this issue among other participants as well). This is why we were allowed to submit, “unofficially”, a supervised version after discussing with the DREAM organizers. Despite violating the DREAM challenge rule, we believe the “unsupervised” method we describe here has been evaluated rigorously and the ideas are valuable, based on both post-challenge analysis results, as well as arguments presented below.
Secondly, we argue that the M2 metric that we proposed is indeed unsupervised instead of supervised learning. In a supervised method, you optimize parameters in order to achieve the minimal deviation from ground truth (or gold standard in this work). Since the gold standard in this work is defined with all 84 genes, when you reduce the number of genes, you expect to gradually increase the gap between the gold standard and the prediction, and the goal is to minimize the gap with K genes. Our proposed metric M2 does not aim to reduce deviation from ground truth. In fact, the values of M2 achieved with the genes that we selected have better M2 values than the initial 84 genes, which potentially indicate that the initial 84 genes are not “optimal”. Another way to look at this is that we do not use the “gold standard” position in determining how good or bad the selected genes are. The definition of M2 relies on lcG , the location bin whose expression profile of gene set G is the most similar to cell c among all location bins. Although initially when G has all 84 genes, lcG is indeed identical to the gold standard, lc* , this set of locations moves away from the gold standard when the gene set changes – so you could say that we have a “moving” gold standard if you wish, and the fact is that with 20 genes, lcG is quite different from lc*. Furthermore, while we implemented a stepwise backward elimination method to choose G genes from 84 genes, we could have started with any random set of genes or the whole RNAseq dataset (with much longer running time, however). In fact, our analysis results showed that the M2 values on test data can often be better than the M2 values on training data, further supporting that this is not a supervised method.

(Q2) The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

(A2) We have included this information in the revised manuscript:
“The running time of PSO algorithm is about 15 hours when running on a system with 16 GB of memory. However, the running time could depend on different optimization settings such as parameter alpha and beta.”

Minor:
(Q3) The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

(A3) M1 and M2 were defined based on Euclidean distances and our objective was indeed to minimize M1+M2, not to maximize it.
We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors describe their approach to the DREAM Single cell prediction challenge that was designed to find optimal subsets of 20, 40, and 60 genes that would allow prediction of single cells locations in a dme embryo with minimal accuracy loss relative to locations based on 84 genes. The method could be useful in similar applications, yet I have the following comments:

Major:
(Q1) The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.

(A1) Firstly, we agree that the “unsupervised” version of our method does not strictly follow the DREAM challenge rule of not using in situ data directly. The reason is that we were not aware of the rule until after our submission. (The rule was posted in the discussion forum instead of on the challenge main webpage, and there were a lot of discussions about this issue among other participants as well). This is why we were allowed to submit, “unofficially”, a supervised version after discussing with the DREAM organizers. Despite violating the DREAM challenge rule, we believe the “unsupervised” method we describe here has been evaluated rigorously and the ideas are valuable, based on both post-challenge analysis results, as well as arguments presented below.
Secondly, we argue that the M2 metric that we proposed is indeed unsupervised instead of supervised learning. In a supervised method, you optimize parameters in order to achieve the minimal deviation from ground truth (or gold standard in this work). Since the gold standard in this work is defined with all 84 genes, when you reduce the number of genes, you expect to gradually increase the gap between the gold standard and the prediction, and the goal is to minimize the gap with K genes. Our proposed metric M2 does not aim to reduce deviation from ground truth. In fact, the values of M2 achieved with the genes that we selected have better M2 values than the initial 84 genes, which potentially indicate that the initial 84 genes are not “optimal”. Another way to look at this is that we do not use the “gold standard” position in determining how good or bad the selected genes are. The definition of M2 relies on lcG , the location bin whose expression profile of gene set G is the most similar to cell c among all location bins. Although initially when G has all 84 genes, lcG is indeed identical to the gold standard, lc* , this set of locations moves away from the gold standard when the gene set changes – so you could say that we have a “moving” gold standard if you wish, and the fact is that with 20 genes, lcG is quite different from lc*. Furthermore, while we implemented a stepwise backward elimination method to choose G genes from 84 genes, we could have started with any random set of genes or the whole RNAseq dataset (with much longer running time, however). In fact, our analysis results showed that the M2 values on test data can often be better than the M2 values on training data, further supporting that this is not a supervised method.

(Q2) The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

(A2) We have included this information in the revised manuscript:
“The running time of PSO algorithm is about 15 hours when running on a system with 16 GB of memory. However, the running time could depend on different optimization settings such as parameter alpha and beta.”

Minor:
(Q3) The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

(A3) M1 and M2 were defined based on Euclidean distances and our objective was indeed to minimize M1+M2, not to maximize it.
Competing Interests: no competing interests Close
Report a concern

Views

Reviewer Report 07 Sep 2020

Tianci Song, Department of Computer Science and Engineering, University of Minnesota, Minneapolis, MN, USA

Rui Kuang, Department of Computer Science and Engineering, University of Minnesota, Twin Cities, Minneapolis, MN, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.26653.r69945

This manuscript describes the methodology the authors employed to perform well in the DREAM Single cell Transcriptomics Challenge. The theme of the challenge is to select a subset of 84 known marker genes to characterize the spatial gene expression patterns in Drosophila embryo. The team developed methods for unsupervised gene selection, supervised gene selection, gene weighting and neighbor-smoothing based prediction of cell location. Overall, the manuscript provides sufficient detail to reproduce the results and some interpretations. It appears some further improvements can be done as follows:

Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).

Is the rationale for developing the new method (or application) clearly explained?

Partly
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational Biology, Machine Learning, Biological Network Analysis, Single-cell Genomics, Spatial Genomics

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however we have significant reservations, as outlined above.

CITE

Report a concern

Author Response 09 Feb 2021

Maryam Zand, Computer science, University of Texas at San Antonio, San Antonio, 78249, USA

09 Feb 2021

Author Response

We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript ... Continue reading We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript describes the methodology the authors employed to perform well in the DREAM Single cell Transcriptomics Challenge. The theme of the challenge is to select a subset of 84 known marker genes to characterize the spatial gene expression patterns in Drosophila embryo. The team developed methods for unsupervised gene selection, supervised gene selection, gene weighting and neighbor-smoothing based prediction of cell location. Overall, the manuscript provides sufficient detail to reproduce the results and some interpretations. It appears some further improvements can be done as follows:

(Q1) Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
(A1) We thank the reviewer for bringing up this important point. It should be noted that as the challenge participants were blind to the evaluation metrics at the time of results submission, which made a direct assessment of the performance of the proposed methods inaccessible, our team did not perform extensive parameter tuning. In the revised manuscript we have provided some insights and reasonings behind the selection of hyperparameter values used in our work. This added information may be used as a general guideline for hyperparameter selection for applying the proposed method to other datasets of similar nature. Nonetheless, it should be mentioned that optimum hyperparameters is problem-specific and may be found through ad hoc tests, sensitivity analysis, and detailed investigations. The following has been added in the manuscript.
“In this work, k is set to 10 because the evaluation of the prediction results is based on 10 best locations for each single cell. Also, based on the number of location bins (n), we believe 10 is a reasonable choice for the number of nearest neighbors.”
“alpha and beta are acceleration coefficients, also referred to as trust parameters. alpha expresses how much confidence a particle has in itself, while beta expresses how much confidence a particle has in its neighboring particles. Particles draw their strength from their cooperative nature and are most effective when alpha and beta coexist in a good balance. Most applications use alpha=beta. Low values for alpha and beta result in smooth particle trajectories, while high values cause more acceleration, with abrupt movement towards or past good regions. In this study we used alpha=beta=0.2, with 200 agents and the maximum number of iterations set to 40. These parameters were manually tuned by observing the values of the fitness function to reach desired search granularity and speed of convergence.”

(Q2) Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
(A2) During the challenge period, each team was given a limited number of attempts to test the success of their proposed approach(es) - evaluation results and ranking of all teams were shown in a leaderboard, with no details of the evaluation metrics. It was made clear that different methods could be used for different sub-challenges. Therefore, it was a natural choice for us to try a diverse combination of the main ingredients of the method for different subproblems to get some insights of these ingredients. During the post-challenge stage, further experiments have been designed by the DREAM organizers for additional insights (see ref. [16]). In this manuscript, we have also added a few baseline approaches to test these components (see Table 1). While we could repeat the whole experiments with a common strategy for all three sub-challenges, we thought it would be best for the readers to see the results in a way consistent with our final results submitted to DREAM challenge. Admittedly, we did not use PSO for sub-challenge 2 because of lack of time towards the end of the competition. The rationale of using neighbor weighting in subchallenge 1 and 2 but not in subchallenge 3 is that as subchallenge 3 used substantially fewer genes, the quality of the location prediction may be relatively low and therefore using gene expression information from the predicted neighbors could actually degrade the final prediction. The revised manuscript now provides some details of these rationales.

(Q3) The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
(A3) In the revised manuscript we have further explained the results presented in Table1 to make it clearer. The metrics used to rank different methods is now explained in section “Evaluation metrics”. The details of formulation and additional explanation can be found in the reference article [16]. Additional discussion of the evaluation results has also been included in the revised manuscript (see below for your convenience).

“Table 1 shows the results of our supervised and unsupervised methods on the three subchallenges, evaluated by the three metrics (s1, s2, and s3) proposed by the DREAM challenge organizers. The details of these metrics are discussed in Method Section “DREAM consortium evaluation metrics”. A more detailed analysis of the results and comparison with other top-performing algorithms are presented in 16 and is not repeated here. To obtain some additional insights of our algorithms’ performance, we present here the results of some variations of our proposed methods. Both our supervised and unsupervised methods have two important components, (1) gene selection, and (2) neighbor-weighted cell location prediction, integral to selecting a set of most informative genes and locating cells based on the information buried in cell neighborhood network topology. To understand the importance of these two components, we designed a set of baseline studies incorporating four experiments. In these experiments, the gene selection strategy was replaced by either selecting genes randomly, or selecting genes expressed in the most number of cells (high degree genes). The neighbor-based reweighting component was also removed in two of these experiments.
The subchallenge scores corresponding to our method (supervised and unsupervised) along with these four baseline studies are listed in Table 1 under the group A and group B, respectively. The method with highest score (s1, s2, s3) in each of the three subchallenges is shown in boldface. It can be seen that the supervised and unsupervised methods (group A) achieved comparable results, and significantly outperformed the baseline approaches (group B) on average, for all three sub-challenges. For subchallenge 3, which is the most difficult task, both of our methods significantly outperformed the baseline approaches in all three metrics. On the other hand, for subchallenge 1, for which the goal is to select 60 genes to best approximate the cell locations determined by 84 genes, random gene selection coupled with neighbor-based reweighting achieved almost the same performance as our unsupervised approach, and is only slightly inferior to the supervised approach. This is understandable because of the extensive overlap between the randomly selected genes and the “optimal” gene set. High degree selection achieved somewhat less accurate results than random selection, indicating that some less frequently expressed genes are important determinants of cell locations. For subchallenge 2, our proposed methods outperformed all four baseline approaches in s2, and three out of the four baseline approaches in s1 and s3. Finally, comparing the four baseline approaches suggest that the neighbor-based reweighting component significantly improved s2, but its impacts on the other two metrics are somewhat mixed. Overall, the significant performance gain in subchallenge 3 compared to random gene selection and high degree gene selection supports that the small set of genes we identified are important for predicting cell locations.”

(Q4) In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
(A4) The original binarized in situ hybridization data is what the first subplot in Figure 4 shows in fact. For other subplots vISH was used because we wanted to compare our results with Distmap which also uses vISH. Moreover, vISH computes the expression pattern for each gene by combining the cell-bin mapping scores with the original normalized gene expression levels.

(Q5) In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).
(A5) In the revised version we have added “Gold standard cell locations” subsection.
“For each of the 1297 cells, the Mathews Correlation Coefficients (MCC) is calculated at each of the 3039 location bins between the binarized 84 RNAseq expression values for the 84 driver genes and the binarized in situ expression values for the same 84 genes. The location bin with the maximum value of MCC score is defined as the gold standard location for each cell.”
We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript describes the methodology the authors employed to perform well in the DREAM Single cell Transcriptomics Challenge. The theme of the challenge is to select a subset of 84 known marker genes to characterize the spatial gene expression patterns in Drosophila embryo. The team developed methods for unsupervised gene selection, supervised gene selection, gene weighting and neighbor-smoothing based prediction of cell location. Overall, the manuscript provides sufficient detail to reproduce the results and some interpretations. It appears some further improvements can be done as follows:

(Q1) Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
(A1) We thank the reviewer for bringing up this important point. It should be noted that as the challenge participants were blind to the evaluation metrics at the time of results submission, which made a direct assessment of the performance of the proposed methods inaccessible, our team did not perform extensive parameter tuning. In the revised manuscript we have provided some insights and reasonings behind the selection of hyperparameter values used in our work. This added information may be used as a general guideline for hyperparameter selection for applying the proposed method to other datasets of similar nature. Nonetheless, it should be mentioned that optimum hyperparameters is problem-specific and may be found through ad hoc tests, sensitivity analysis, and detailed investigations. The following has been added in the manuscript.
“In this work, k is set to 10 because the evaluation of the prediction results is based on 10 best locations for each single cell. Also, based on the number of location bins (n), we believe 10 is a reasonable choice for the number of nearest neighbors.”
“alpha and beta are acceleration coefficients, also referred to as trust parameters. alpha expresses how much confidence a particle has in itself, while beta expresses how much confidence a particle has in its neighboring particles. Particles draw their strength from their cooperative nature and are most effective when alpha and beta coexist in a good balance. Most applications use alpha=beta. Low values for alpha and beta result in smooth particle trajectories, while high values cause more acceleration, with abrupt movement towards or past good regions. In this study we used alpha=beta=0.2, with 200 agents and the maximum number of iterations set to 40. These parameters were manually tuned by observing the values of the fitness function to reach desired search granularity and speed of convergence.”

(Q2) Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
(A2) During the challenge period, each team was given a limited number of attempts to test the success of their proposed approach(es) - evaluation results and ranking of all teams were shown in a leaderboard, with no details of the evaluation metrics. It was made clear that different methods could be used for different sub-challenges. Therefore, it was a natural choice for us to try a diverse combination of the main ingredients of the method for different subproblems to get some insights of these ingredients. During the post-challenge stage, further experiments have been designed by the DREAM organizers for additional insights (see ref. [16]). In this manuscript, we have also added a few baseline approaches to test these components (see Table 1). While we could repeat the whole experiments with a common strategy for all three sub-challenges, we thought it would be best for the readers to see the results in a way consistent with our final results submitted to DREAM challenge. Admittedly, we did not use PSO for sub-challenge 2 because of lack of time towards the end of the competition. The rationale of using neighbor weighting in subchallenge 1 and 2 but not in subchallenge 3 is that as subchallenge 3 used substantially fewer genes, the quality of the location prediction may be relatively low and therefore using gene expression information from the predicted neighbors could actually degrade the final prediction. The revised manuscript now provides some details of these rationales.

(Q3) The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
(A3) In the revised manuscript we have further explained the results presented in Table1 to make it clearer. The metrics used to rank different methods is now explained in section “Evaluation metrics”. The details of formulation and additional explanation can be found in the reference article [16]. Additional discussion of the evaluation results has also been included in the revised manuscript (see below for your convenience).

“Table 1 shows the results of our supervised and unsupervised methods on the three subchallenges, evaluated by the three metrics (s1, s2, and s3) proposed by the DREAM challenge organizers. The details of these metrics are discussed in Method Section “DREAM consortium evaluation metrics”. A more detailed analysis of the results and comparison with other top-performing algorithms are presented in 16 and is not repeated here. To obtain some additional insights of our algorithms’ performance, we present here the results of some variations of our proposed methods. Both our supervised and unsupervised methods have two important components, (1) gene selection, and (2) neighbor-weighted cell location prediction, integral to selecting a set of most informative genes and locating cells based on the information buried in cell neighborhood network topology. To understand the importance of these two components, we designed a set of baseline studies incorporating four experiments. In these experiments, the gene selection strategy was replaced by either selecting genes randomly, or selecting genes expressed in the most number of cells (high degree genes). The neighbor-based reweighting component was also removed in two of these experiments.
The subchallenge scores corresponding to our method (supervised and unsupervised) along with these four baseline studies are listed in Table 1 under the group A and group B, respectively. The method with highest score (s1, s2, s3) in each of the three subchallenges is shown in boldface. It can be seen that the supervised and unsupervised methods (group A) achieved comparable results, and significantly outperformed the baseline approaches (group B) on average, for all three sub-challenges. For subchallenge 3, which is the most difficult task, both of our methods significantly outperformed the baseline approaches in all three metrics. On the other hand, for subchallenge 1, for which the goal is to select 60 genes to best approximate the cell locations determined by 84 genes, random gene selection coupled with neighbor-based reweighting achieved almost the same performance as our unsupervised approach, and is only slightly inferior to the supervised approach. This is understandable because of the extensive overlap between the randomly selected genes and the “optimal” gene set. High degree selection achieved somewhat less accurate results than random selection, indicating that some less frequently expressed genes are important determinants of cell locations. For subchallenge 2, our proposed methods outperformed all four baseline approaches in s2, and three out of the four baseline approaches in s1 and s3. Finally, comparing the four baseline approaches suggest that the neighbor-based reweighting component significantly improved s2, but its impacts on the other two metrics are somewhat mixed. Overall, the significant performance gain in subchallenge 3 compared to random gene selection and high degree gene selection supports that the small set of genes we identified are important for predicting cell locations.”

(Q4) In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
(A4) The original binarized in situ hybridization data is what the first subplot in Figure 4 shows in fact. For other subplots vISH was used because we wanted to compare our results with Distmap which also uses vISH. Moreover, vISH computes the expression pattern for each gene by combining the cell-bin mapping scores with the original normalized gene expression levels.

(Q5) In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).
(A5) In the revised version we have added “Gold standard cell locations” subsection.
“For each of the 1297 cells, the Mathews Correlation Coefficients (MCC) is calculated at each of the 3039 location bins between the binarized 84 RNAseq expression values for the 84 driver genes and the binarized in situ expression values for the same 84 genes. The location bin with the maximum value of MCC score is defined as the gold standard location for each cell.”
Competing Interests: No competing interesets Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 09 Feb 2021

Maryam Zand, Computer science, University of Texas at San Antonio, San Antonio, 78249, USA

09 Feb 2021

Author Response

We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript ... Continue reading We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript describes the methodology the authors employed to perform well in the DREAM Single cell Transcriptomics Challenge. The theme of the challenge is to select a subset of 84 known marker genes to characterize the spatial gene expression patterns in Drosophila embryo. The team developed methods for unsupervised gene selection, supervised gene selection, gene weighting and neighbor-smoothing based prediction of cell location. Overall, the manuscript provides sufficient detail to reproduce the results and some interpretations. It appears some further improvements can be done as follows:

(Q1) Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
(A1) We thank the reviewer for bringing up this important point. It should be noted that as the challenge participants were blind to the evaluation metrics at the time of results submission, which made a direct assessment of the performance of the proposed methods inaccessible, our team did not perform extensive parameter tuning. In the revised manuscript we have provided some insights and reasonings behind the selection of hyperparameter values used in our work. This added information may be used as a general guideline for hyperparameter selection for applying the proposed method to other datasets of similar nature. Nonetheless, it should be mentioned that optimum hyperparameters is problem-specific and may be found through ad hoc tests, sensitivity analysis, and detailed investigations. The following has been added in the manuscript.
“In this work, k is set to 10 because the evaluation of the prediction results is based on 10 best locations for each single cell. Also, based on the number of location bins (n), we believe 10 is a reasonable choice for the number of nearest neighbors.”
“alpha and beta are acceleration coefficients, also referred to as trust parameters. alpha expresses how much confidence a particle has in itself, while beta expresses how much confidence a particle has in its neighboring particles. Particles draw their strength from their cooperative nature and are most effective when alpha and beta coexist in a good balance. Most applications use alpha=beta. Low values for alpha and beta result in smooth particle trajectories, while high values cause more acceleration, with abrupt movement towards or past good regions. In this study we used alpha=beta=0.2, with 200 agents and the maximum number of iterations set to 40. These parameters were manually tuned by observing the values of the fitness function to reach desired search granularity and speed of convergence.”

(Q2) Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
(A2) During the challenge period, each team was given a limited number of attempts to test the success of their proposed approach(es) - evaluation results and ranking of all teams were shown in a leaderboard, with no details of the evaluation metrics. It was made clear that different methods could be used for different sub-challenges. Therefore, it was a natural choice for us to try a diverse combination of the main ingredients of the method for different subproblems to get some insights of these ingredients. During the post-challenge stage, further experiments have been designed by the DREAM organizers for additional insights (see ref. [16]). In this manuscript, we have also added a few baseline approaches to test these components (see Table 1). While we could repeat the whole experiments with a common strategy for all three sub-challenges, we thought it would be best for the readers to see the results in a way consistent with our final results submitted to DREAM challenge. Admittedly, we did not use PSO for sub-challenge 2 because of lack of time towards the end of the competition. The rationale of using neighbor weighting in subchallenge 1 and 2 but not in subchallenge 3 is that as subchallenge 3 used substantially fewer genes, the quality of the location prediction may be relatively low and therefore using gene expression information from the predicted neighbors could actually degrade the final prediction. The revised manuscript now provides some details of these rationales.

(Q3) The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
(A3) In the revised manuscript we have further explained the results presented in Table1 to make it clearer. The metrics used to rank different methods is now explained in section “Evaluation metrics”. The details of formulation and additional explanation can be found in the reference article [16]. Additional discussion of the evaluation results has also been included in the revised manuscript (see below for your convenience).

“Table 1 shows the results of our supervised and unsupervised methods on the three subchallenges, evaluated by the three metrics (s1, s2, and s3) proposed by the DREAM challenge organizers. The details of these metrics are discussed in Method Section “DREAM consortium evaluation metrics”. A more detailed analysis of the results and comparison with other top-performing algorithms are presented in 16 and is not repeated here. To obtain some additional insights of our algorithms’ performance, we present here the results of some variations of our proposed methods. Both our supervised and unsupervised methods have two important components, (1) gene selection, and (2) neighbor-weighted cell location prediction, integral to selecting a set of most informative genes and locating cells based on the information buried in cell neighborhood network topology. To understand the importance of these two components, we designed a set of baseline studies incorporating four experiments. In these experiments, the gene selection strategy was replaced by either selecting genes randomly, or selecting genes expressed in the most number of cells (high degree genes). The neighbor-based reweighting component was also removed in two of these experiments.
The subchallenge scores corresponding to our method (supervised and unsupervised) along with these four baseline studies are listed in Table 1 under the group A and group B, respectively. The method with highest score (s1, s2, s3) in each of the three subchallenges is shown in boldface. It can be seen that the supervised and unsupervised methods (group A) achieved comparable results, and significantly outperformed the baseline approaches (group B) on average, for all three sub-challenges. For subchallenge 3, which is the most difficult task, both of our methods significantly outperformed the baseline approaches in all three metrics. On the other hand, for subchallenge 1, for which the goal is to select 60 genes to best approximate the cell locations determined by 84 genes, random gene selection coupled with neighbor-based reweighting achieved almost the same performance as our unsupervised approach, and is only slightly inferior to the supervised approach. This is understandable because of the extensive overlap between the randomly selected genes and the “optimal” gene set. High degree selection achieved somewhat less accurate results than random selection, indicating that some less frequently expressed genes are important determinants of cell locations. For subchallenge 2, our proposed methods outperformed all four baseline approaches in s2, and three out of the four baseline approaches in s1 and s3. Finally, comparing the four baseline approaches suggest that the neighbor-based reweighting component significantly improved s2, but its impacts on the other two metrics are somewhat mixed. Overall, the significant performance gain in subchallenge 3 compared to random gene selection and high degree gene selection supports that the small set of genes we identified are important for predicting cell locations.”

(Q4) In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
(A4) The original binarized in situ hybridization data is what the first subplot in Figure 4 shows in fact. For other subplots vISH was used because we wanted to compare our results with Distmap which also uses vISH. Moreover, vISH computes the expression pattern for each gene by combining the cell-bin mapping scores with the original normalized gene expression levels.

(Q5) In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).
(A5) In the revised version we have added “Gold standard cell locations” subsection.
“For each of the 1297 cells, the Mathews Correlation Coefficients (MCC) is calculated at each of the 3039 location bins between the binarized 84 RNAseq expression values for the 84 driver genes and the binarized in situ expression values for the same 84 genes. The location bin with the maximum value of MCC score is defined as the gold standard location for each cell.”
We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript describes the methodology the authors employed to perform well in the DREAM Single cell Transcriptomics Challenge. The theme of the challenge is to select a subset of 84 known marker genes to characterize the spatial gene expression patterns in Drosophila embryo. The team developed methods for unsupervised gene selection, supervised gene selection, gene weighting and neighbor-smoothing based prediction of cell location. Overall, the manuscript provides sufficient detail to reproduce the results and some interpretations. It appears some further improvements can be done as follows:

(Q1) Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
(A1) We thank the reviewer for bringing up this important point. It should be noted that as the challenge participants were blind to the evaluation metrics at the time of results submission, which made a direct assessment of the performance of the proposed methods inaccessible, our team did not perform extensive parameter tuning. In the revised manuscript we have provided some insights and reasonings behind the selection of hyperparameter values used in our work. This added information may be used as a general guideline for hyperparameter selection for applying the proposed method to other datasets of similar nature. Nonetheless, it should be mentioned that optimum hyperparameters is problem-specific and may be found through ad hoc tests, sensitivity analysis, and detailed investigations. The following has been added in the manuscript.
“In this work, k is set to 10 because the evaluation of the prediction results is based on 10 best locations for each single cell. Also, based on the number of location bins (n), we believe 10 is a reasonable choice for the number of nearest neighbors.”
“alpha and beta are acceleration coefficients, also referred to as trust parameters. alpha expresses how much confidence a particle has in itself, while beta expresses how much confidence a particle has in its neighboring particles. Particles draw their strength from their cooperative nature and are most effective when alpha and beta coexist in a good balance. Most applications use alpha=beta. Low values for alpha and beta result in smooth particle trajectories, while high values cause more acceleration, with abrupt movement towards or past good regions. In this study we used alpha=beta=0.2, with 200 agents and the maximum number of iterations set to 40. These parameters were manually tuned by observing the values of the fitness function to reach desired search granularity and speed of convergence.”

(Q2) Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
(A2) During the challenge period, each team was given a limited number of attempts to test the success of their proposed approach(es) - evaluation results and ranking of all teams were shown in a leaderboard, with no details of the evaluation metrics. It was made clear that different methods could be used for different sub-challenges. Therefore, it was a natural choice for us to try a diverse combination of the main ingredients of the method for different subproblems to get some insights of these ingredients. During the post-challenge stage, further experiments have been designed by the DREAM organizers for additional insights (see ref. [16]). In this manuscript, we have also added a few baseline approaches to test these components (see Table 1). While we could repeat the whole experiments with a common strategy for all three sub-challenges, we thought it would be best for the readers to see the results in a way consistent with our final results submitted to DREAM challenge. Admittedly, we did not use PSO for sub-challenge 2 because of lack of time towards the end of the competition. The rationale of using neighbor weighting in subchallenge 1 and 2 but not in subchallenge 3 is that as subchallenge 3 used substantially fewer genes, the quality of the location prediction may be relatively low and therefore using gene expression information from the predicted neighbors could actually degrade the final prediction. The revised manuscript now provides some details of these rationales.

(Q3) The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
(A3) In the revised manuscript we have further explained the results presented in Table1 to make it clearer. The metrics used to rank different methods is now explained in section “Evaluation metrics”. The details of formulation and additional explanation can be found in the reference article [16]. Additional discussion of the evaluation results has also been included in the revised manuscript (see below for your convenience).

“Table 1 shows the results of our supervised and unsupervised methods on the three subchallenges, evaluated by the three metrics (s1, s2, and s3) proposed by the DREAM challenge organizers. The details of these metrics are discussed in Method Section “DREAM consortium evaluation metrics”. A more detailed analysis of the results and comparison with other top-performing algorithms are presented in 16 and is not repeated here. To obtain some additional insights of our algorithms’ performance, we present here the results of some variations of our proposed methods. Both our supervised and unsupervised methods have two important components, (1) gene selection, and (2) neighbor-weighted cell location prediction, integral to selecting a set of most informative genes and locating cells based on the information buried in cell neighborhood network topology. To understand the importance of these two components, we designed a set of baseline studies incorporating four experiments. In these experiments, the gene selection strategy was replaced by either selecting genes randomly, or selecting genes expressed in the most number of cells (high degree genes). The neighbor-based reweighting component was also removed in two of these experiments.
The subchallenge scores corresponding to our method (supervised and unsupervised) along with these four baseline studies are listed in Table 1 under the group A and group B, respectively. The method with highest score (s1, s2, s3) in each of the three subchallenges is shown in boldface. It can be seen that the supervised and unsupervised methods (group A) achieved comparable results, and significantly outperformed the baseline approaches (group B) on average, for all three sub-challenges. For subchallenge 3, which is the most difficult task, both of our methods significantly outperformed the baseline approaches in all three metrics. On the other hand, for subchallenge 1, for which the goal is to select 60 genes to best approximate the cell locations determined by 84 genes, random gene selection coupled with neighbor-based reweighting achieved almost the same performance as our unsupervised approach, and is only slightly inferior to the supervised approach. This is understandable because of the extensive overlap between the randomly selected genes and the “optimal” gene set. High degree selection achieved somewhat less accurate results than random selection, indicating that some less frequently expressed genes are important determinants of cell locations. For subchallenge 2, our proposed methods outperformed all four baseline approaches in s2, and three out of the four baseline approaches in s1 and s3. Finally, comparing the four baseline approaches suggest that the neighbor-based reweighting component significantly improved s2, but its impacts on the other two metrics are somewhat mixed. Overall, the significant performance gain in subchallenge 3 compared to random gene selection and high degree gene selection supports that the small set of genes we identified are important for predicting cell locations.”

(Q4) In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
(A4) The original binarized in situ hybridization data is what the first subplot in Figure 4 shows in fact. For other subplots vISH was used because we wanted to compare our results with Distmap which also uses vISH. Moreover, vISH computes the expression pattern for each gene by combining the cell-bin mapping scores with the original normalized gene expression levels.

(Q5) In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).
(A5) In the revised version we have added “Gold standard cell locations” subsection.
“For each of the 1297 cells, the Mathews Correlation Coefficients (MCC) is calculated at each of the 3039 location bins between the binarized 84 RNAseq expression values for the 84 driver genes and the binarized in situ expression values for the same 84 genes. The location bin with the maximum value of MCC score is defined as the gold standard location for each cell.”
Competing Interests: No competing interesets Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 20 Aug 2020

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 09 Feb 21	read	read
Version 1 20 Aug 20	read	read

Tianci Song, University of Minnesota, Minneapolis, USA

Rui Kuang, University of Minnesota, Twin Cities, Minneapolis, USA
Adi Tarca, Wayne State University, Detroit, USA

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

4 Views

23 Mar 2021 | for Version 2

Tianci Song, Department of Computer Science and Engineering, University of Minnesota, Minneapolis, MN, USA

Rui Kuang, Department of Computer Science and Engineering, University of Minnesota, Twin Cities, Minneapolis, MN, USA

4 Views Cite this report Responses(0)

Approved

The authors have addressed all the raised concerns in this revision.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational Biology, Machine Learning, Biological Network Analysis, Single-cell Genomics, Spatial Genomics

We confirm that we have read this submission and believe that we have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

3 Views

18 Feb 2021 | for Version 2

Adi Tarca, Department of Computer Science, College of Engineering, Wayne State University, Detroit, MI, USA

3 Views Cite this report Responses(0)

Approved

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Machine learning, genomics, statistics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

18 Views

18 Sep 2020 | for Version 1

Adi Tarca, Department of Computer Science, College of Engineering, Wayne State University, Detroit, MI, USA

18 Views Cite this report Responses(1)

Approved With Reservations

The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.
The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

Minor:

The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

Is the rationale for developing the new method (or application) clearly explained?

Partly
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Machine learning, genomics, statistics.

Respond to this report

Responses (1)

Author Response

09 Feb 2021

Maryam Zand, Computer science, University of Texas at San Antonio, San Antonio, 78249, USA

We thank the reviewer for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer2 comments
The authors describe their approach to the DREAM Single cell prediction challenge that was designed to find optimal subsets of 20, 40, and 60 genes that would allow prediction of single cells locations in a dme embryo with minimal accuracy loss relative to locations based on 84 genes. The method could be useful in similar applications, yet I have the following comments:

Major:
(Q1) The “Unsupervised gene selection” section defines two metrics (M1 and M2) to assess the quality a given gene set G of size 20, 40, or 60 out of all 84 genes with in situ data available. The optimal set of genes is identified by a greedy algorithm. However, metric M2 can not be considered unsupervised because it takes the samples from the set where prediction of locations are expected (cells from the scRNA-seq data) and correlates their expression values with profiles of all in situ bins and finds those genes that ensure a maximum correlation. While the authors do not use the information of the in situ cell assigned by DistMap to a given single cell (gold standard), by expecting that there should be some 10 bins with gene expression patterns that correlate with the profile of each single cell, they are implicitly creating their own gold standard. Therefore, not only M2 should be stated as supervised instead of unsupervised, the authors should add as a limitation in the discussion the fact that they have used in situ data from all 84 genes in selecting the best subsets of 20, 40, 60 which was against the DREAM challenge rules.

(A1) Firstly, we agree that the “unsupervised” version of our method does not strictly follow the DREAM challenge rule of not using in situ data directly. The reason is that we were not aware of the rule until after our submission. (The rule was posted in the discussion forum instead of on the challenge main webpage, and there were a lot of discussions about this issue among other participants as well). This is why we were allowed to submit, “unofficially”, a supervised version after discussing with the DREAM organizers. Despite violating the DREAM challenge rule, we believe the “unsupervised” method we describe here has been evaluated rigorously and the ideas are valuable, based on both post-challenge analysis results, as well as arguments presented below.
Secondly, we argue that the M2 metric that we proposed is indeed unsupervised instead of supervised learning. In a supervised method, you optimize parameters in order to achieve the minimal deviation from ground truth (or gold standard in this work). Since the gold standard in this work is defined with all 84 genes, when you reduce the number of genes, you expect to gradually increase the gap between the gold standard and the prediction, and the goal is to minimize the gap with K genes. Our proposed metric M2 does not aim to reduce deviation from ground truth. In fact, the values of M2 achieved with the genes that we selected have better M2 values than the initial 84 genes, which potentially indicate that the initial 84 genes are not “optimal”. Another way to look at this is that we do not use the “gold standard” position in determining how good or bad the selected genes are. The definition of M2 relies on lcG , the location bin whose expression profile of gene set G is the most similar to cell c among all location bins. Although initially when G has all 84 genes, lcG is indeed identical to the gold standard, lc* , this set of locations moves away from the gold standard when the gene set changes – so you could say that we have a “moving” gold standard if you wish, and the fact is that with 20 genes, lcG is quite different from lc*. Furthermore, while we implemented a stepwise backward elimination method to choose G genes from 84 genes, we could have started with any random set of genes or the whole RNAseq dataset (with much longer running time, however). In fact, our analysis results showed that the M2 values on test data can often be better than the M2 values on training data, further supporting that this is not a supervised method.

(Q2) The PSO algorithm to set the gene weights optimization seems to be computationally intensive. Can the authors provide some sense of computation time involved?

(A2) We have included this information in the revised manuscript:
“The running time of PSO algorithm is about 15 hours when running on a system with 16 GB of memory. However, the running time could depend on different optimization settings such as parameter alpha and beta.”

Minor:
(Q3) The authors state, “We used a standard backward elimination algorithm to identify a subset of genes G with the minimal sum of M1 and M2”. I believe they meant identifying the subset of genes G with a minimal loss (decrease) in M1+M2, since you want the sum to remain as high as possible. So in the end this is a maximization not minimization problem.

(A3) M1 and M2 were defined based on Euclidean distances and our objective was indeed to minimize M1+M2, not to maximize it.

View more View less

Competing Interests

no competing interests

Back to all reports

Reviewer Report

24 Views

07 Sep 2020 | for Version 1

Tianci Song, Department of Computer Science and Engineering, University of Minnesota, Minneapolis, MN, USA

Rui Kuang, Department of Computer Science and Engineering, University of Minnesota, Twin Cities, Minneapolis, MN, USA

24 Views Cite this report Responses(1)

Approved With Reservations

Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).

Is the rationale for developing the new method (or application) clearly explained?

Partly
Is the description of the method technically sound?

Yes
Are sufficient details provided to allow replication of the method development and its use by others?

Yes
If any results are presented, are all the source data underlying the results available to ensure full reproducibility?

Yes
Are the conclusions about the method and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational Biology, Machine Learning, Biological Network Analysis, Single-cell Genomics, Spatial Genomics

Respond to this report

Responses (1)

Author Response

09 Feb 2021

Maryam Zand, Computer science, University of Texas at San Antonio, San Antonio, 78249, USA

We thank the reviewers for the overall positive comments, as well as the detailed critics that have helped to improve the manuscript.

Response to Reviewer1 comments
This manuscript describes the methodology the authors employed to perform well in the DREAM Single cell Transcriptomics Challenge. The theme of the challenge is to select a subset of 84 known marker genes to characterize the spatial gene expression patterns in Drosophila embryo. The team developed methods for unsupervised gene selection, supervised gene selection, gene weighting and neighbor-smoothing based prediction of cell location. Overall, the manuscript provides sufficient detail to reproduce the results and some interpretations. It appears some further improvements can be done as follows:

(Q1) Where it is understood that the team has optimized the hyper-parameter including k, alpha and beta with some fixed values for this dataset. For others to use the same methods on other similar studies, there is no clue how to tune or select the hyper-parameters. Discussion or more experimental results should be provided in this regard.
(A1) We thank the reviewer for bringing up this important point. It should be noted that as the challenge participants were blind to the evaluation metrics at the time of results submission, which made a direct assessment of the performance of the proposed methods inaccessible, our team did not perform extensive parameter tuning. In the revised manuscript we have provided some insights and reasonings behind the selection of hyperparameter values used in our work. This added information may be used as a general guideline for hyperparameter selection for applying the proposed method to other datasets of similar nature. Nonetheless, it should be mentioned that optimum hyperparameters is problem-specific and may be found through ad hoc tests, sensitivity analysis, and detailed investigations. The following has been added in the manuscript.
“In this work, k is set to 10 because the evaluation of the prediction results is based on 10 best locations for each single cell. Also, based on the number of location bins (n), we believe 10 is a reasonable choice for the number of nearest neighbors.”
“alpha and beta are acceleration coefficients, also referred to as trust parameters. alpha expresses how much confidence a particle has in itself, while beta expresses how much confidence a particle has in its neighboring particles. Particles draw their strength from their cooperative nature and are most effective when alpha and beta coexist in a good balance. Most applications use alpha=beta. Low values for alpha and beta result in smooth particle trajectories, while high values cause more acceleration, with abrupt movement towards or past good regions. In this study we used alpha=beta=0.2, with 200 agents and the maximum number of iterations set to 40. These parameters were manually tuned by observing the values of the fitness function to reach desired search granularity and speed of convergence.”

(Q2) Similarly, it is also a mystery why different strategies of combining the methods are necessary for the three sub-challenges. There is no discussion of how the combinations are selected or optimized.
(A2) During the challenge period, each team was given a limited number of attempts to test the success of their proposed approach(es) - evaluation results and ranking of all teams were shown in a leaderboard, with no details of the evaluation metrics. It was made clear that different methods could be used for different sub-challenges. Therefore, it was a natural choice for us to try a diverse combination of the main ingredients of the method for different subproblems to get some insights of these ingredients. During the post-challenge stage, further experiments have been designed by the DREAM organizers for additional insights (see ref. [16]). In this manuscript, we have also added a few baseline approaches to test these components (see Table 1). While we could repeat the whole experiments with a common strategy for all three sub-challenges, we thought it would be best for the readers to see the results in a way consistent with our final results submitted to DREAM challenge. Admittedly, we did not use PSO for sub-challenge 2 because of lack of time towards the end of the competition. The rationale of using neighbor weighting in subchallenge 1 and 2 but not in subchallenge 3 is that as subchallenge 3 used substantially fewer genes, the quality of the location prediction may be relatively low and therefore using gene expression information from the predicted neighbors could actually degrade the final prediction. The revised manuscript now provides some details of these rationales.

(Q3) The results in Table 1 are very poorly explained. How to calculate the 14%, 20%, 30% improvement over the three measures is unexplained. Possibly, it is also helpful to explain the metric used to rank different methods in the competition.
(A3) In the revised manuscript we have further explained the results presented in Table1 to make it clearer. The metrics used to rank different methods is now explained in section “Evaluation metrics”. The details of formulation and additional explanation can be found in the reference article [16]. Additional discussion of the evaluation results has also been included in the revised manuscript (see below for your convenience).

“Table 1 shows the results of our supervised and unsupervised methods on the three subchallenges, evaluated by the three metrics (s1, s2, and s3) proposed by the DREAM challenge organizers. The details of these metrics are discussed in Method Section “DREAM consortium evaluation metrics”. A more detailed analysis of the results and comparison with other top-performing algorithms are presented in 16 and is not repeated here. To obtain some additional insights of our algorithms’ performance, we present here the results of some variations of our proposed methods. Both our supervised and unsupervised methods have two important components, (1) gene selection, and (2) neighbor-weighted cell location prediction, integral to selecting a set of most informative genes and locating cells based on the information buried in cell neighborhood network topology. To understand the importance of these two components, we designed a set of baseline studies incorporating four experiments. In these experiments, the gene selection strategy was replaced by either selecting genes randomly, or selecting genes expressed in the most number of cells (high degree genes). The neighbor-based reweighting component was also removed in two of these experiments.
The subchallenge scores corresponding to our method (supervised and unsupervised) along with these four baseline studies are listed in Table 1 under the group A and group B, respectively. The method with highest score (s1, s2, s3) in each of the three subchallenges is shown in boldface. It can be seen that the supervised and unsupervised methods (group A) achieved comparable results, and significantly outperformed the baseline approaches (group B) on average, for all three sub-challenges. For subchallenge 3, which is the most difficult task, both of our methods significantly outperformed the baseline approaches in all three metrics. On the other hand, for subchallenge 1, for which the goal is to select 60 genes to best approximate the cell locations determined by 84 genes, random gene selection coupled with neighbor-based reweighting achieved almost the same performance as our unsupervised approach, and is only slightly inferior to the supervised approach. This is understandable because of the extensive overlap between the randomly selected genes and the “optimal” gene set. High degree selection achieved somewhat less accurate results than random selection, indicating that some less frequently expressed genes are important determinants of cell locations. For subchallenge 2, our proposed methods outperformed all four baseline approaches in s2, and three out of the four baseline approaches in s1 and s3. Finally, comparing the four baseline approaches suggest that the neighbor-based reweighting component significantly improved s2, but its impacts on the other two metrics are somewhat mixed. Overall, the significant performance gain in subchallenge 3 compared to random gene selection and high degree gene selection supports that the small set of genes we identified are important for predicting cell locations.”

(Q4) In Figure 4, why not also plot the original in-situ hybridization and scRNAseq expressions of the three genes for comparison? The use of vISH seems to be unnecessary.
(A4) The original binarized in situ hybridization data is what the first subplot in Figure 4 shows in fact. For other subplots vISH was used because we wanted to compare our results with Distmap which also uses vISH. Moreover, vISH computes the expression pattern for each gene by combining the cell-bin mapping scores with the original normalized gene expression levels.

(Q5) In the section "Datasets and pre-processing steps", a subsection explaining the "gold standard" prediction by DistMap should be added. It is confusing in the description of supervised vs unsupervised gene selection, when the DistMap prediction and the nearest locations are used in the measures in equation (2) and (3).
(A5) In the revised version we have added “Gold standard cell locations” subsection.
“For each of the 1297 cells, the Mathews Correlation Coefficients (MCC) is calculated at each of the 3039 location bins between the binarized 84 RNAseq expression values for the 84 driver genes and the binarized in situ expression values for the same 84 genes. The location bin with the maximum value of MCC score is defined as the gold standard location for each cell.”

View more View less

Competing Interests

No competing interesets

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] 1. Kolodziejczyk AA, Kim JK, Svensson V, et al.: The Technology and Biology of Single-Cell RNA Sequencing. Mol Cell. 2015; 58(4): 610–620. PubMed Abstract | Publisher Full Text

[2] 2. Altschuler SJ, Wu LF: Cellular Heterogeneity: Do Differences Make a Difference? Cell. 2010; 141(4): 559–563. PubMed Abstract | Publisher Full Text | Free Full Text

[3] 3. Tang F, Barbacioru C, Wang Y, et al.: mRNA-Seq whole-transcriptome analysis of a single cell. Nat Methods. 2009; 6(5): 377–382. PubMed Abstract | Publisher Full Text

[4] 4. Wang Z, Gerstein M, Snyder M: RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet. 2009; 10(1): 57–63. PubMed Abstract | Publisher Full Text | Free Full Text

[5] 5. Meamardoost S, Bhattacharya M, Hwang EJ, et al.: FARCI: Fast and Robust Connectome Inference. bioRxiv. 2020. Publisher Full Text

[6] 6. Huang S: Non-genetic heterogeneity of cells in development: more than just noise. Development. 2009; 136(23): 3853–3862. PubMed Abstract | Publisher Full Text | Free Full Text

[7] 7. Shalek AK, Satija R, Shuga J, et al.: Single-cell RNA-seq reveals dynamic paracrine control of cellular variation. Nature. 2014; 510(7505): 363–369. PubMed Abstract | Publisher Full Text | Free Full Text

[8] 8. Wagner A, Regev A, Yosef N: Revealing the vectors of cellular identity with single-cell genomics. Nat Biotechnol. 2016; 34(11): 1145–1160. PubMed Abstract | Publisher Full Text | Free Full Text

[9] 9. Casasent AK, Schalck A, Gao R, et al.: Multiclonal Invasion in Breast Tumors Identified by Topographic Single Cell Sequencing. Cell. 2018; 172(1–2): 205–217.e12. PubMed Abstract | Publisher Full Text | Free Full Text

[10] 10. Ståhl PL, Salmén F, Vickovic S, et al.: Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science. 2016; 353(6294): 78–82. PubMed Abstract | Publisher Full Text

[11] 11. Lovatt D, Ruble BK, Lee J, et al.: Transcriptome in vivo analysis (TIVA) of spatially defined single cells in live tissue. Nat Methods. 2014; 11(2): 190–196. PubMed Abstract | Publisher Full Text | Free Full Text

[12] 12. Rodriques SG, Stickels RR, Goeva A, et al.: Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science. 2019; 363(6434): 1463–1467. PubMed Abstract | Publisher Full Text | Free Full Text

[13] 13. Oh SW, Harris JA, Ng L, et al.: A mesoscale connectome of the mouse brain. Nature. 2014; 508(7495): 207–214. PubMed Abstract | Publisher Full Text | Free Full Text

[14] 14. Hawrylycz MJ, Lein ES, Guillozet-Bongaarts AL, et al.: An anatomically comprehensive atlas of the adult human brain transcriptome. Nature. 2012; 489(7416): 391–399. PubMed Abstract | Publisher Full Text | Free Full Text

[15] 15. Satija R, Farrell JA, Gennert D, et al.: Spatial reconstruction of single-cell gene expression data. Nat Biotechnol. 2015; 33(5): 495–502. PubMed Abstract | Publisher Full Text | Free Full Text

[16] 16. Karaiskos N, Wahle P, Alles J, et al.: The Drosophila embryo at single-cell transcriptome resolution. Science. 2017; 358(6360): 194–199. PubMed Abstract | Publisher Full Text

[17] 17. Tanevski J, Nguyen T, Truong B, et al.: Gene selection for optimal prediction of cell position in tissues from single-cell transcriptomics data. Life Sci Alliance. 2020; 3(11): e202000867. PubMed Abstract | Publisher Full Text | Free Full Text

[18] 18. Zand M, Ruan J: mary77/scspatialmapping: First release of scspatialmapping. Zenodo. 2020. http://www.doi.org/10.5281/zenodo.3877577

[19] 19. Huang M, Wang J, Torre E, et al.: SAVER: gene expression recovery for single-cell RNA sequencing. Nat Methods. 2018; 15(7): 539–542. PubMed Abstract | Publisher Full Text | Free Full Text

[20] 20. Zand M, Ruan J: Network-based single-cell rna-seq data imputation enhances cell type identification. Genes (Basel). 2020; 11(4): 377. PubMed Abstract | Publisher Full Text | Free Full Text

[21] 21. Stauber M, Lemke S, Schmidt-Ott U: Expression and regulation of caudal in the lower cyclorrhaphan fly megaselia. Dev Genes Evol. 2008; 218(2): 81–87. PubMed Abstract | Publisher Full Text | Free Full Text

[22] 22. Lim B, Fukaya T, Heist T, et al.: Temporal dynamics of pair-rule stripes in living drosophila embryos. Proc Natl Acad Sci U S A. 2018; 115(33): 8376–8381. PubMed Abstract | Publisher Full Text | Free Full Text

Spatial mapping of single cells in the Drosophila embryo from transcriptomic data based on topological consistency

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Methods

Overview of the proposed method

Datasets and pre-processing steps

Finding most informative genes

Unsupervised gene selection

Supervised gene selection

Supervised learning to find optimal gene weights

Neighbor-weighted cell location prediction

How proposed method applied to different subchallenges

Post-challenge phase

DREAM consortium evaluation metrics

Software

Results and discussion

Performance evaluation

Table 1. Numerical values of subchallenges scores are given for the ease of comparison with some designed baseline methods.

Robustness of marker genes

Figure 1. Boxplot shows the Jaccard similarity between the genes selected for each of the 10 CV scheme in all 3 subchallenges.

Figure 2. The Venn diagram shows 20 genes selected from supervised and unsupervised methods out of which 11 genes are common for both methods.

Recovering gene expression pattern

Figure 3. Histogram of correlation between gene patterns predicted by our method and DistMap using 60,40,20 genes.

Figure 4. Expression pattern of three sample genes are given for in situ, DistMap, and our method using 60,40,20 genes.

Conclusion

Data availability

Underlying data

Software availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated