<i>Seqpare</i>: a novel metric of similarity between genomic interval sets

Selena C. Feng; Nathan C. Sheffield; Jianglin Feng

doi:10.12688/f1000research.23390.2

Home Browse Seqpare: a novel metric of similarity between genomic interval sets

ALL Metrics

Views

Downloads

Get PDF

Get XML

Export

▬

✚

Software Tool Article

Revised

Seqpare: a novel metric of similarity between genomic interval sets

[version 2; peer review: 2 approved]

Previously titled: Seqpare: a self-consistent metric of similarity between genomic interval sets

Selena C. Feng¹, Nathan C. Sheffield², Jianglin Feng ^2,3

PUBLISHED 04 Jan 2021

Author details Author details

¹ Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, 02139, USA
² Center for Public Health Genomics, University of Virginia, Charlottesville, VA, USA
³ Deepstanding LLC, Crozet, VA, 22932, USA

Selena C. Feng
Roles: Methodology, Software, Validation, Writing – Review & Editing

Nathan C. Sheffield
Roles: Conceptualization, Writing – Review & Editing

Jianglin Feng
Roles: Conceptualization, Methodology, Software, Supervision, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

OPEN PEER REVIEW

REVIEWER STATUS

This article is included in the Bioinformatics gateway.

This article is included in the Cell & Molecular Biology gateway.

Abstract

Searching genomic interval sets produced by sequencing methods has been widely and routinely performed; however, existing metrics for quantifying similarities among interval sets are inconsistent. Here we introduce Seqpare, a self-consistent and effective metric of similarity and tool for comparing sequences based on their interval sets. With this metric, the similarity of two interval sets is quantified by a single index, the ratio of their effective overlap over the union: an index of zero indicates unrelated interval sets, and an index of one means that the interval sets are identical. Analysis and tests confirm the effectiveness and self-consistency of the Seqpare metric.

Keywords

Genome analysis, interval set, similarity metric, sequence comparison, algorithm

Corresponding author: Jianglin Feng

Competing interests: No competing interests were disclosed.

Grant information: The author(s) declared that no grants were involved in supporting this work.

Copyright: © 2021 Feng SC et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

How to cite: Feng SC, Sheffield NC and Feng J. Seqpare: a novel metric of similarity between genomic interval sets [version 2; peer review: 2 approved]. F1000Research 2021, 9:581 (https://doi.org/10.12688/f1000research.23390.2) First published: 09 Jun 2020, 9:581 (https://doi.org/10.12688/f1000research.23390.1) Latest published: 04 Jan 2021, 9:581 (https://doi.org/10.12688/f1000research.23390.2)

Revised Amendments from Version 1

A few minor changes are made to the text according to the suggestions of the reviewers. The title word 'self-consistent' is replaced with 'novel'. A small subset of the test data and instructions are added to the software page to ease the verification of the main result.

See the authors' detailed response to the review by Zhaohui Steve Qin
See the authors' detailed response to the review by Burcak Otlu

Introduction

Functional genomic data are often summarized as interval sets and deposited in public repositories (e.g., UCSC, ENCODE, Roadmap, GEO, SRA etc.). Identifying relationships among sequences and searching through widely available sequence data are routine tasks in genomic research. A fundamental operation in genomic/epigenomic analysis is comparing two interval sets, and many algorithms and tools have been developed for this purpose (Alekseyenko & Lee, 2007; Cormen et al., 2001; Feng et al., 2019; Giardine et al., 2005; Jalili et al., 2019; Kent et al., 2002; Li, 2011; Neph et al., 2012; Quinlan & Hall, 2010; Richardson, 2006). These methods are based on computing the total number of intersections (overlaps) between the two interval sets. To compare a query interval set with multiple interval sets in a genomic sequence database, searching tools LOLA (Sheffield & Bock, 2016) and GIGGLE (Layer et al., 2018) calculate two values — Fisher’s exact p-value and the odds-ratio based on the total number of intersections — and use them as the similarity score to rank the search results. These similarity metrics have proven useful for determining relationships among interval sets, but also have some flaws. First, calculating the Fisher’s exact test results requires building a contingency table, but determining its values is not straightforward. The p-value and odds-ratio for two intervals sets (with number of intervals N₁ and N₂) are calculated from four numbers, namely, the number of intersections between the two sets, n, the number of intervals in set 1 that do not overlap an interval in set 2, N₁ - n, the number of intervals in set 2 that do not overlap an interval in set 1, N₂ - n, and the number of intervals that are not present in either set, m. Determining the value of the fourth number m is not straightforward; in LOLA, it depends on the definition of a “universe set” that is not objectively defined, whereas GIGGLE estimates m from the two interval sets. Second, the total number of overlaps n does not necessarily reflect similarity since intervals can have very different lengths (often in the range of 1 to 10⁵ base pairs) and two very different intervals may intersect by only a few base pairs. This can result in inconsistency of the metrics: a comparison between two identical interval sets may have a larger p-value or smaller odds-ratio than a comparison between two different interval sets (see example cases and analysis in the next section). More strikingly, since one interval may contain or cover other intervals in an interval set, depending on how the overlaps are computed, n can be larger than N₁ and/or N₂, i.e., N₁-n and/or N₂-n can be negative, which leads to both the p-value and odds-ratio being undefined—another potential source of inconsistency. Third, the Fisher’s exact-based metrics require two values (p-value and odds-ratio) but neither is a direct measurement of the similarity: p-values are sensitive to the total number of regions and can range as low as 10^-200 for large genomic interval sets, and odds-ratios are sensitive to small numbers; and neither metric directly informs on how similar the two sets are. Last, the p-value calculation is computationally expensive for genomic interval sets, particularly when the number of intervals is large (up to 10⁹). To overcome these weaknesses of the Fisher’s exact-based metrics, we developed Seqpare, a self-consistent metric for quantifying the similarity among genomic interval sets.

Methods

Seqpare metric

The Seqpare metric uses a single index to quantify the degree of similarity S of two interval sets with number of intervals N₁ and N₂. Similar to the Jaccard index, the Seqpare metric is directly defined as the ratio of the total effective overlap O of the two interval sets over the union N₁+N₂ - O:

S = O / (N_{1} + N_{2} - O) (1)

For two intervals v₁ in set 1 and v₂ in set 2, the similarity s is defined as:

s = o / (l_{1} + l_{2} - o) (2)

where o is the length of the intersection and l₁ and l₂ are the lengths of v₁ and v₂ respectively. Definition 2 is the Jaccard index for individual intervals: o represents the effective overlap of the two intervals and s takes values in the range of [0, 1]: s = 0 indicates that there is no overlap between the two intervals, and s = 1 means that the union equals the overlap so v₁ and v₂ are identical. Then the total effective overlap O for the two interval sets can be calculated by adding up the similarities of all mutual best matching (MBM) pairs:

O = \sum s_{M B M} (3)

A MBM pair is defined as a pair of intervals v₁ and v₂ that fulfill the following conditions: among all intervals in set 2 that intersect v₁, v₂ matches v₁ the best, i.e., the similarity s between v₁ and v₂ is the highest among those intersections; and among all intervals in set 1 that intersect v₂, v₁ matches v₂ the best. Clearly, if two intervals only intersect each other, then they form an MBM pair. In Figure 1a, the two long intervals (the 1st in set 1 and the 1st in set 2) only intersect each other (intersection pair ip_1,1), so they form an MBM pair; similarly, the two short intervals ip_2,2 form another MBM pair. For intervals that involve multiple intersections, we define a relatively simple and strict rule to find the MBM pairs: find and choose the first MBM pair that has the highest s among all involved intersection pairs, then find and choose the next MBM pair that has the highest s from the rest of the intersection pairs (excluding all pairs that involve the intervals that are already chosen), and so on until there are no more intersection pairs. In Figure 1b, there are 3 intersection pairs: ip_1,2 with s=1/5, ip_1,3 with s=1/9, and ip_2,3 with s=1/5. So the first MBM pair is either ip_1,2 or ip₂_,3 depending on which one is found first. If ip_1,2 is chosen as the first MBM pair, then ip_1,3 will not be considered since interval 1 in set 1 is already chosen, and then we have only ip_2,3 left, which is the second MBM pair. We get the same result if ip_2,3 is chosen as the first MBM pair. In Figure 1d, there are 6 intersection pairs and two MBM pairs: ip_1,1 and ip_3,2 both with s=1, where interval 2 in set 1 (i_2,1) does not have a match. Note that interval i_2,1 matches best with interval i_1,2, but i_1,2 does not match best with i_2,1, so they are not the mutual best matching pair.

Figure 1. Example cases for illustrating the Seqpare similarity metric.

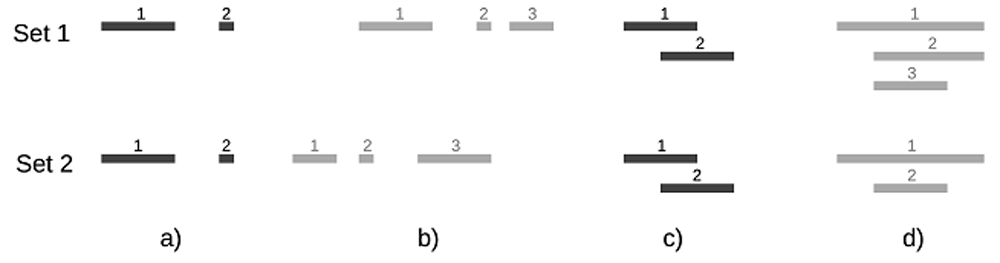
The length ratio of the short interval to the longer intervals are 1: 5 in a), 1: 3: 5 in b), and 2: 3 :4 in d). The total number of overlaps n is 2 for a), 3 for b) (interval 1 in Set 1 intersects two intervals in Set 2), 4 for c) and 6 for d). The p-value in case b is smaller than that in case a. N₁ - n and N₂ - n are both negative in cases c and d.

Since the number of total matching pairs ≤ Min(N₁, N₂) — the minimum of N₁ and N₂ — and s is in range of [0, 1], we obtain O ≤ Min(N₁, N₂), and S takes a value in the range of [0, 1]. If S is zero, then there is no matching pair, and vice versa; if S = 1, then N₁ = N₂ = O (the two sets are equivalent), and vice versa. And, because each s is the mutual best match, O is symmetric (the amount of overlap between set 1 and set 2 is the same as that between set 2 to set 1) and so is S.

In Figure 1a, O_a=2 and S_a=1, which is correct because the two sets are identical. In Figure 1b, O_b=2/5 and S_b=1/14, which is expected since the two sets are very different. The Fisher’s exact approach is inconsistent here: the p-value in 1b is smaller than that in 1a although the two sets in 1b are very different while those in 1a are equivalent. Assuming that the number of intervals N in the ‘universe set’ is 100, then Fisher’s exact test contingency table is [(2, 0), (0, 98)] in 1a and [(3, 0), (0, 97)] in 1b, which gives p_a = 2.02×10^-4 and p_b = 6.18×10^-6 respectively. The odds-ratio is ∞ in both cases. In Figure 1c and Figure 1d, N₁- n and N₂- n are all negative, so it is not conceptually appropriate to use Fisher’s exact test to calculate the p-value and odds-ratio.

Implementation

The implementation of the Seqpare metric is simple. The searching for MBM pairs is deterministic and it can be implemented by directly following the description in the above section. The Seqpare code is built on top of the AIList v0.0.1 (Feng et al., 2019) software written in C.

Operation

The Seqpare software (Feng & Feng, 2020) was tested on Linux machines and the minimum required memory is 8GB. The interval set file should be in the format of bed or bed.gz.

Results

A test with real genomic interval sets

To test Seqpare and compare it with the Fisher’s exact-based metrics, we took 100 interval sets from a UCSC database and used one interval set, affyGnf1h, as a query to search over the database. Because the database contains the query set, affyGnf1h should have the highest similarity score. Table 1 (Feng & Feng, 2020) shows part of the result. Interval set affyGnf1h indeed ranks first with maximum similarity 1 when using Seqpare, but it ranks 94^th out of 100 when using the p-value and ranks last when using the odds-ratio. This happens because N₁-n and N₂-n are both negative (n=16686, N₁=N₂=12158). Given this inconsistency, GIGGLE sets negative N₁-n and N₂-n to zero to calculate the p-value, and to one to calculate the odds-ratio. The Seqpare indices for other interval sets are all small (<0.03) because the average effective overlap of an intersection pair in those sets is about 0.1 or less, i.e., they are very different from the query set affyGnf1h; however, all of the p-values are so small (e^-200), which suggests that the p-value is not a meaningful similarity index for these genomic interval sets. This search takes 6m30s for Seqpare and 15m32s for GIGGLE. All computations were carried out on a computer with a 2.8GHz CPU, 16GB memory, and an external SSD hard disk. The complete results can be found at the same site as the software.

Table 1. Comparison of Seqpare and GIGGLE similarity metrics: partial list of the search results from a collection of 100 interval sets, which contains the query set affyGnf1h.

Seqpare metric		p-value and odds-ratio				Interval dataset file name
rank	similarity	rank_p	p-value	rank_or	odds-ratio	Interval dataset file name
1	1.0	94	1.543 e^-197	100	9.046 e^-16	affyGnf1h
2	0.029	19	8.328 e^-201	1	25.25	ccdsGene
3	0.026	35	2.743 e^-200	3	4.425	allenBrainAli
4	0.022	39	3.372 e^-200	32	7.972 e^-11	affyU133Plus2
5	0.021	4	5.403 e^-202	2	17.24	affyU133

Conclusion

We have shown that the Fisher’s exact test approach may be not the most appropriate test statistic for comparing similarity among interval sets. While the approach has been shown to be successful for many questions, we have demonstrated how it can break down for a variety of reasons, such as very similar interval sets, within-set containment, widely varying interval lengths among sets, or small effective overlaps. In contrast, Seqpare is a self-consistent metric for quantifying the similarity of two interval sets that addresses these concerns. Seqpare is the first rigorously defined metric for comparing two sequences based on their interval sets. In addition to the metric itself, our Seqpare software tool provides functions for both searching and mapping large-scale interval datasets. We anticipate that this approach will contribute to novel results for interval set searching.

Data availability

Source data

Test data of interval sets are from http://hgdownload.cse.ucsc.edu/goldenPath/hg19/database

A small subset of the test data and instructions are provided for verifying the result: https://github.com/deepstanding/seqpare/ucsc_30

Underlying data

Zenodo: deepstanding/seqpare: First release of Seqpare. http://doi.org/10.5281/zenodo.3840051 (Feng & Feng, 2020)

This project contains the following underlying data:

- AffyGnf1h_ucsc100_seqpare (Seqpare similarity result)
- AffyGnf1h_ucsc100_giggle (GIGGLE p-value and odds-ratio result)

Data is available alongside the source code under the terms of the MIT license.

Software availability

Source code available from: https://github.com/deepstanding/seqpare

Archived source code at time of publication: http://doi.org/10.5281/zenodo.3840051 (Feng & Feng, 2020)

License: MIT

Faculty Opinions recommended

References

Alekseyenko AV, Lee CJ: Nested containment list (NCList): A new algorithm for accelerating interval query of genome alignment and interval databases. Bioinformatics. 2007; 23(11): 1386–93. PubMed Abstract | Publisher Full Text
Cormen TH, Leiserson CE, Rivest RL, et al.: Introduction to algorithms second edition. 2001. Reference Source
Feng S, Feng J: deepstanding/seqpare: First release of Seqpare (Version v1.0.0). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.3840051
Feng J, Ratan A, Sheffield NC: Augmented interval list: A novel data structure for efficient genomic interval search. Bioinfomatics. 2019; 35(23): 4907–4911. Publisher Full Text
Giardine B, Riemer C, Hardison RC, et al.: Galaxy: A platform for interactive large-scale genome analysis. Genome Res. 2005; 15(10): 1451–5. PubMed Abstract | Publisher Full Text | Free Full Text
Jalili V, Matteucci M, Goecks J, et al.: Next generation indexing for genomic intervals. IEEE Transactions on Knowledge and Data Engineering. 2019; 31(10): 2008–2021. Publisher Full Text
Kent WJ, Sugnet CW, Furey TS, et al.: The human genome browser at ucsc. Genome Res. 2002; 12(6): 996–1006. PubMed Abstract | Publisher Full Text | Free Full Text
Layer RM, Pedersen BS, DiSera T, et al.: GIGGLE: A Search Engine for Large-Scale Integrated Genome Analysis. Nat Methods. 2018; 15(2): 123–126. PubMed Abstract | Publisher Full Text | Free Full Text
Li H: Tabix: Fast Retrieval of Sequence Features From Generic TAB-delimited Files. Bioinformatics. 2011; 27(5): 718–9. PubMed Abstract | Publisher Full Text | Free Full Text
Neph S, Kuehn MS, Reynolds AP, et al.: BEDOPS: high-performance genomic feature operations. Bioinformatics. 2012; 28(14): 1919–1920. PubMed Abstract | Publisher Full Text | Free Full Text
Quinlan AR, Hall IM: BEDTools: A flexible suite of utilities for comparing genomic features. Bioinformatics. 2010; 26(6): 841–842. PubMed Abstract | Publisher Full Text | Free Full Text
Richardson JE: Fjoin: Simple and efficient computation of feature overlaps. J Comput Biol. 2006; 13(8): 1457–1464. PubMed Abstract | Publisher Full Text
Sheffield NC, Bock C: LOLA: Enrichment analysis for genomic region sets and regulatory elements in R and bioconductor. Bioinformatics. 2016; 32(4): 587–589. PubMed Abstract | Publisher Full Text | Free Full Text

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 09 Jun 2020

Author details Author details

Selena C. Feng
Roles: Methodology, Software, Validation, Writing – Review & Editing

Nathan C. Sheffield
Roles: Conceptualization, Writing – Review & Editing

Jianglin Feng
Roles: Conceptualization, Methodology, Software, Supervision, Validation, Writing – Original Draft Preparation, Writing – Review & Editing

Competing interests

No competing interests were disclosed.

Grant information

The author(s) declared that no grants were involved in supporting this work.

Article Versions (2)

version 2

Revised

Published: 04 Jan 2021, 9:581

https://doi.org/10.12688/f1000research.23390.2

version 1

Published: 09 Jun 2020, 9:581

https://doi.org/10.12688/f1000research.23390.1

© 2021 Feng SC et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Download

Export To

metrics

	Views	Downloads
F1000Research	-	-
PubMed Central Data from PMC are received and updated monthly.	-	-

Citations

SEE MORE DETAILS

CITE

how to cite this article

Feng SC, Sheffield NC and Feng J. Seqpare: a novel metric of similarity between genomic interval sets [version 2; peer review: 2 approved]. F1000Research 2021, 9:581 (https://doi.org/10.12688/f1000research.23390.2)

NOTE: If applicable, it is important to ensure the information in square brackets after the title is included in all citations of this article.

track

receive updates on this article

Track an article to receive email alerts on any updates to this article.

Open Peer Review

Version 2

VERSION 2

PUBLISHED 04 Jan 2021

Revised

Views

Reviewer Report 13 Jan 2021

Zhaohui Steve Qin, Department of Biostatistics and Bioinformatics, Rollins School of Public Health, Emory University, Atlanta, GA, USA

Approved

https://doi.org/10.5256/f1000research.31408.r76397

No ... Continue reading

CITE

Report a concern

Respond or Comment

Version 1

VERSION 1

PUBLISHED 09 Jun 2020

Views

Reviewer Report 11 Nov 2020

Burcak Otlu, Department of Cellular and Molecular Medicine and Department of Bioengineering and Moores Cancer Center, University of California, San Diego, La Jolla, CA, USA

Approved

https://doi.org/10.5256/f1000research.25817.r71030

The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.

I wonder what is the time complexity of MBM calculation? Does this metric work when there are self-contained intervals (overlapping intervals) in each interval set?
Why you choose this metric instead of simply using jaccard index?

In the text, "6 ips" is written. It would be better to explain "ips" before its usage.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Computational biology, cancer genomics, bioinformatics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

CITE

Report a concern

Author Response 04 Jan 2021

John Feng, Deepstanding LLC, Crozet, 22932, USA

04 Jan 2021

Author Response

Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
... Continue reading Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
Response: Thank you for this positive comment.

Comment: I wonder what is the time complexity of MBM calculation? Does this metric work when there are self-contained intervals (overlapping intervals) in each interval set?
Why you choose this metric instead of simply using jaccard index?
Response: Thanks for the insightful comments.
1. Seqpare finds all intersections (total m) by using AIList algorithm with time complexity of O(n log n), where n is the number of intervals in the datasets. The MBM algorithm calculates the similarities of these intersection pairs and then finds the MBM pairs one by one. The time complexity of MBM depends on the cases. If all intersection pairs are simple (Figure 1a), then the complexity is O(m); in the worst case (Figure 1c or Figure 1d), all intersection pairs are correlated and the complexity is
O(m²). For most real genomic interval sets, the time complexity is close to O(m).
2. Seqpare is a general metric of similarity and it works when there are self-contained intervals. Figure 1c and 1d are two cases of self-contained interval sets, where seqpare works well but the p-value based metric breaks down. Also, most of the UCSC interval sets used in this paper contain large number of overlapping intervals.
3. Jaccard index is defined as the ratio of Intersection over Union and it takes value in the range of [0, 1], i.e., the Intersection is never larger than the Union and the Union is never zero or negative. Jaccard index can be strictly used for two individual intervals, as explained in the Metric section of the paper. However, it cannot be used directly as similarity metric for two interval sets.
For two interval sets, the simple Jaccard metric would be J = N/(N1+N2-N), where N1 and N2 are the number of intervals in the two interval sets, and N is the number of intersections between them. However, the ‘Intersection’ N can be larger than the ‘Union’ (N1+N2-N), and (N1+N2-N) can also be zero or negative: in Figure 1c, N=4, N1=2, N2=2, and (N1+N2-N) is zero; in Figure 1d, N=6, N1=2, N2=3, (N1+N2-N) is -1. Therefore, just like the p-value, simple Jaccard index is not a rigorous similarity metric for interval sets. This also suggests that using p-value or simple Jaccard index to compare interval sets can be misleading and defining a rigorous similarity metric for interval sets is challenging.

Comment: In the text, "6 ips" is written. It would be better to explain "ips" before its usage.
Response: We replaced it as ‘6 intersection pairs’.
Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
Response: Thank you for this positive comment.

Comment: I wonder what is the time complexity of MBM calculation? Does this metric work when there are self-contained intervals (overlapping intervals) in each interval set?
Why you choose this metric instead of simply using jaccard index?
Response: Thanks for the insightful comments.
1. Seqpare finds all intersections (total m) by using AIList algorithm with time complexity of O(n log n), where n is the number of intervals in the datasets. The MBM algorithm calculates the similarities of these intersection pairs and then finds the MBM pairs one by one. The time complexity of MBM depends on the cases. If all intersection pairs are simple (Figure 1a), then the complexity is O(m); in the worst case (Figure 1c or Figure 1d), all intersection pairs are correlated and the complexity is
O(m²). For most real genomic interval sets, the time complexity is close to O(m).
2. Seqpare is a general metric of similarity and it works when there are self-contained intervals. Figure 1c and 1d are two cases of self-contained interval sets, where seqpare works well but the p-value based metric breaks down. Also, most of the UCSC interval sets used in this paper contain large number of overlapping intervals.
3. Jaccard index is defined as the ratio of Intersection over Union and it takes value in the range of [0, 1], i.e., the Intersection is never larger than the Union and the Union is never zero or negative. Jaccard index can be strictly used for two individual intervals, as explained in the Metric section of the paper. However, it cannot be used directly as similarity metric for two interval sets.
For two interval sets, the simple Jaccard metric would be J = N/(N1+N2-N), where N1 and N2 are the number of intervals in the two interval sets, and N is the number of intersections between them. However, the ‘Intersection’ N can be larger than the ‘Union’ (N1+N2-N), and (N1+N2-N) can also be zero or negative: in Figure 1c, N=4, N1=2, N2=2, and (N1+N2-N) is zero; in Figure 1d, N=6, N1=2, N2=3, (N1+N2-N) is -1. Therefore, just like the p-value, simple Jaccard index is not a rigorous similarity metric for interval sets. This also suggests that using p-value or simple Jaccard index to compare interval sets can be misleading and defining a rigorous similarity metric for interval sets is challenging.

Comment: In the text, "6 ips" is written. It would be better to explain "ips" before its usage.
Response: We replaced it as ‘6 intersection pairs’.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 04 Jan 2021

John Feng, Deepstanding LLC, Crozet, 22932, USA

04 Jan 2021

Author Response

Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
... Continue reading Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
Response: Thank you for this positive comment.

Comment: I wonder what is the time complexity of MBM calculation? Does this metric work when there are self-contained intervals (overlapping intervals) in each interval set?
Why you choose this metric instead of simply using jaccard index?
Response: Thanks for the insightful comments.
1. Seqpare finds all intersections (total m) by using AIList algorithm with time complexity of O(n log n), where n is the number of intervals in the datasets. The MBM algorithm calculates the similarities of these intersection pairs and then finds the MBM pairs one by one. The time complexity of MBM depends on the cases. If all intersection pairs are simple (Figure 1a), then the complexity is O(m); in the worst case (Figure 1c or Figure 1d), all intersection pairs are correlated and the complexity is
O(m²). For most real genomic interval sets, the time complexity is close to O(m).
2. Seqpare is a general metric of similarity and it works when there are self-contained intervals. Figure 1c and 1d are two cases of self-contained interval sets, where seqpare works well but the p-value based metric breaks down. Also, most of the UCSC interval sets used in this paper contain large number of overlapping intervals.
3. Jaccard index is defined as the ratio of Intersection over Union and it takes value in the range of [0, 1], i.e., the Intersection is never larger than the Union and the Union is never zero or negative. Jaccard index can be strictly used for two individual intervals, as explained in the Metric section of the paper. However, it cannot be used directly as similarity metric for two interval sets.
For two interval sets, the simple Jaccard metric would be J = N/(N1+N2-N), where N1 and N2 are the number of intervals in the two interval sets, and N is the number of intersections between them. However, the ‘Intersection’ N can be larger than the ‘Union’ (N1+N2-N), and (N1+N2-N) can also be zero or negative: in Figure 1c, N=4, N1=2, N2=2, and (N1+N2-N) is zero; in Figure 1d, N=6, N1=2, N2=3, (N1+N2-N) is -1. Therefore, just like the p-value, simple Jaccard index is not a rigorous similarity metric for interval sets. This also suggests that using p-value or simple Jaccard index to compare interval sets can be misleading and defining a rigorous similarity metric for interval sets is challenging.

Comment: In the text, "6 ips" is written. It would be better to explain "ips" before its usage.
Response: We replaced it as ‘6 intersection pairs’.
Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
Response: Thank you for this positive comment.

Comment: I wonder what is the time complexity of MBM calculation? Does this metric work when there are self-contained intervals (overlapping intervals) in each interval set?
Why you choose this metric instead of simply using jaccard index?
Response: Thanks for the insightful comments.
1. Seqpare finds all intersections (total m) by using AIList algorithm with time complexity of O(n log n), where n is the number of intervals in the datasets. The MBM algorithm calculates the similarities of these intersection pairs and then finds the MBM pairs one by one. The time complexity of MBM depends on the cases. If all intersection pairs are simple (Figure 1a), then the complexity is O(m); in the worst case (Figure 1c or Figure 1d), all intersection pairs are correlated and the complexity is
O(m²). For most real genomic interval sets, the time complexity is close to O(m).
2. Seqpare is a general metric of similarity and it works when there are self-contained intervals. Figure 1c and 1d are two cases of self-contained interval sets, where seqpare works well but the p-value based metric breaks down. Also, most of the UCSC interval sets used in this paper contain large number of overlapping intervals.
3. Jaccard index is defined as the ratio of Intersection over Union and it takes value in the range of [0, 1], i.e., the Intersection is never larger than the Union and the Union is never zero or negative. Jaccard index can be strictly used for two individual intervals, as explained in the Metric section of the paper. However, it cannot be used directly as similarity metric for two interval sets.
For two interval sets, the simple Jaccard metric would be J = N/(N1+N2-N), where N1 and N2 are the number of intervals in the two interval sets, and N is the number of intersections between them. However, the ‘Intersection’ N can be larger than the ‘Union’ (N1+N2-N), and (N1+N2-N) can also be zero or negative: in Figure 1c, N=4, N1=2, N2=2, and (N1+N2-N) is zero; in Figure 1d, N=6, N1=2, N2=3, (N1+N2-N) is -1. Therefore, just like the p-value, simple Jaccard index is not a rigorous similarity metric for interval sets. This also suggests that using p-value or simple Jaccard index to compare interval sets can be misleading and defining a rigorous similarity metric for interval sets is challenging.

Comment: In the text, "6 ips" is written. It would be better to explain "ips" before its usage.
Response: We replaced it as ‘6 intersection pairs’.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Views

Reviewer Report 30 Jul 2020

Zhaohui Steve Qin, Department of Biostatistics and Bioinformatics, Rollins School of Public Health, Emory University, Atlanta, GA, USA

Approved with Reservations

https://doi.org/10.5256/f1000research.25817.r66632

Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked an important problem to work on and they presented a nice solution. The performance, from their ... Continue reading

I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Figure 1C is not mentioned in the paper. Not sure why.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests: No competing interests were disclosed.

Reviewer Expertise: Bioinformatics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

CITE

Report a concern

Author Response 04 Jan 2021

John Feng, Deepstanding LLC, Crozet, 22932, USA

04 Jan 2021

Author Response

Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked ... Continue reading Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked an important problem to work on and they presented a nice solution. The performance, from their studies, seem quite impressive. It is a nice new tool for solving such problems. but I do have a few issues with the paper.
Response: Thank you for your helpful comments and suggestions. We have revised the paper according to the specific comments, and we have also added a subset of the test data and instructions to the software page to ease the verification of the result.

Comment: I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Response: The word "self-consistent" is used here with its literal meaning of "not having parts or aspects which are in conflict or contradiction with each other" (google dictionary). Being self-consistent is necessary for a definition, concept, metric or theory. We think it's a useful word and we have explained it in the Introduction. Nevertheless, we did remove it from the title since it may cause confusion without context.

Comment: Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Response: Genomic intervals in the standard BED file format contain essential genomic information such as Chromosome, start coordinate, end coordinate and strand, etc. Like all other tools mentioned in the paper, Seqpare uses BED file format. Seqpare does not require the intervals to be sorted, which is an advantage over tools that do require intervals to be sorted.

Comment: Figure 1C is not mentioned in the paper. Not sure why.
Response: Figure 1 shows four cases and Figure 1c is mentioned as case c in the last paragraph of the Methods section "Seqpare metric". We replaced ‘case c’ with ‘Figure 1c’.
Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked an important problem to work on and they presented a nice solution. The performance, from their studies, seem quite impressive. It is a nice new tool for solving such problems. but I do have a few issues with the paper.
Response: Thank you for your helpful comments and suggestions. We have revised the paper according to the specific comments, and we have also added a subset of the test data and instructions to the software page to ease the verification of the result.

Comment: I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Response: The word "self-consistent" is used here with its literal meaning of "not having parts or aspects which are in conflict or contradiction with each other" (google dictionary). Being self-consistent is necessary for a definition, concept, metric or theory. We think it's a useful word and we have explained it in the Introduction. Nevertheless, we did remove it from the title since it may cause confusion without context.

Comment: Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Response: Genomic intervals in the standard BED file format contain essential genomic information such as Chromosome, start coordinate, end coordinate and strand, etc. Like all other tools mentioned in the paper, Seqpare uses BED file format. Seqpare does not require the intervals to be sorted, which is an advantage over tools that do require intervals to be sorted.

Comment: Figure 1C is not mentioned in the paper. Not sure why.
Response: Figure 1 shows four cases and Figure 1c is mentioned as case c in the last paragraph of the Methods section "Seqpare metric". We replaced ‘case c’ with ‘Figure 1c’.
Competing Interests: No competing interests were disclosed. Close
Report a concern
Respond or Comment

COMMENTS ON THIS REPORT

Author Response 04 Jan 2021

John Feng, Deepstanding LLC, Crozet, 22932, USA

04 Jan 2021

Author Response

Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked ... Continue reading Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked an important problem to work on and they presented a nice solution. The performance, from their studies, seem quite impressive. It is a nice new tool for solving such problems. but I do have a few issues with the paper.
Response: Thank you for your helpful comments and suggestions. We have revised the paper according to the specific comments, and we have also added a subset of the test data and instructions to the software page to ease the verification of the result.

Comment: I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Response: The word "self-consistent" is used here with its literal meaning of "not having parts or aspects which are in conflict or contradiction with each other" (google dictionary). Being self-consistent is necessary for a definition, concept, metric or theory. We think it's a useful word and we have explained it in the Introduction. Nevertheless, we did remove it from the title since it may cause confusion without context.

Comment: Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Response: Genomic intervals in the standard BED file format contain essential genomic information such as Chromosome, start coordinate, end coordinate and strand, etc. Like all other tools mentioned in the paper, Seqpare uses BED file format. Seqpare does not require the intervals to be sorted, which is an advantage over tools that do require intervals to be sorted.

Comment: Figure 1C is not mentioned in the paper. Not sure why.
Response: Figure 1 shows four cases and Figure 1c is mentioned as case c in the last paragraph of the Methods section "Seqpare metric". We replaced ‘case c’ with ‘Figure 1c’.
Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked an important problem to work on and they presented a nice solution. The performance, from their studies, seem quite impressive. It is a nice new tool for solving such problems. but I do have a few issues with the paper.
Response: Thank you for your helpful comments and suggestions. We have revised the paper according to the specific comments, and we have also added a subset of the test data and instructions to the software page to ease the verification of the result.

Comment: I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Response: The word "self-consistent" is used here with its literal meaning of "not having parts or aspects which are in conflict or contradiction with each other" (google dictionary). Being self-consistent is necessary for a definition, concept, metric or theory. We think it's a useful word and we have explained it in the Introduction. Nevertheless, we did remove it from the title since it may cause confusion without context.

Comment: Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Response: Genomic intervals in the standard BED file format contain essential genomic information such as Chromosome, start coordinate, end coordinate and strand, etc. Like all other tools mentioned in the paper, Seqpare uses BED file format. Seqpare does not require the intervals to be sorted, which is an advantage over tools that do require intervals to be sorted.

Comment: Figure 1C is not mentioned in the paper. Not sure why.
Response: Figure 1 shows four cases and Figure 1c is mentioned as case c in the last paragraph of the Methods section "Seqpare metric". We replaced ‘case c’ with ‘Figure 1c’.
Competing Interests: No competing interests were disclosed. Close
Report a concern

Comments on this article Comments (0)

Version 2

VERSION 2 PUBLISHED 09 Jun 2020

Open Peer Review

Reviewer Status

Reviewer Reports

	Invited Reviewers
	1	2
Version 2 (revision) 04 Jan 21	read
Version 1 09 Jun 20	read	read

Zhaohui Steve Qin, Emory University, Atlanta, USA
Burcak Otlu, University of California, San Diego, La Jolla, USA

Comments on this article

All Comments(0)

Add a comment

Browse by related subjects

Back to all reports

Reviewer Report

8 Views

13 Jan 2021 | for Version 2

Zhaohui Steve Qin, Department of Biostatistics and Bioinformatics, Rollins School of Public Health, Emory University, Atlanta, GA, USA

8 Views Cite this report Responses(0)

Approved

No more questions.

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Bioinformatics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (0)

Back to all reports

Reviewer Report

23 Views

11 Nov 2020 | for Version 1

Burcak Otlu, Department of Cellular and Molecular Medicine and Department of Bioengineering and Moores Cancer Center, University of California, San Diego, La Jolla, CA, USA

23 Views Cite this report Responses(1)

Approved

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Yes
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Yes

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Computational biology, cancer genomics, bioinformatics.

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

Respond to this report

Responses (1)

Author Response

04 Jan 2021

John Feng, Deepstanding LLC, Crozet, 22932, USA

Comment: The authors have defined a similarity metric for defining similarity between two interval sets. They have justified well why this metric is better than Fisher's exact p-value and odds-ratio.
Response: Thank you for this positive comment.

Comment: I wonder what is the time complexity of MBM calculation? Does this metric work when there are self-contained intervals (overlapping intervals) in each interval set?
Why you choose this metric instead of simply using jaccard index?
Response: Thanks for the insightful comments.
1. Seqpare finds all intersections (total m) by using AIList algorithm with time complexity of O(n log n), where n is the number of intervals in the datasets. The MBM algorithm calculates the similarities of these intersection pairs and then finds the MBM pairs one by one. The time complexity of MBM depends on the cases. If all intersection pairs are simple (Figure 1a), then the complexity is O(m); in the worst case (Figure 1c or Figure 1d), all intersection pairs are correlated and the complexity is
O(m²). For most real genomic interval sets, the time complexity is close to O(m).
2. Seqpare is a general metric of similarity and it works when there are self-contained intervals. Figure 1c and 1d are two cases of self-contained interval sets, where seqpare works well but the p-value based metric breaks down. Also, most of the UCSC interval sets used in this paper contain large number of overlapping intervals.
3. Jaccard index is defined as the ratio of Intersection over Union and it takes value in the range of [0, 1], i.e., the Intersection is never larger than the Union and the Union is never zero or negative. Jaccard index can be strictly used for two individual intervals, as explained in the Metric section of the paper. However, it cannot be used directly as similarity metric for two interval sets.
For two interval sets, the simple Jaccard metric would be J = N/(N1+N2-N), where N1 and N2 are the number of intervals in the two interval sets, and N is the number of intersections between them. However, the ‘Intersection’ N can be larger than the ‘Union’ (N1+N2-N), and (N1+N2-N) can also be zero or negative: in Figure 1c, N=4, N1=2, N2=2, and (N1+N2-N) is zero; in Figure 1d, N=6, N1=2, N2=3, (N1+N2-N) is -1. Therefore, just like the p-value, simple Jaccard index is not a rigorous similarity metric for interval sets. This also suggests that using p-value or simple Jaccard index to compare interval sets can be misleading and defining a rigorous similarity metric for interval sets is challenging.

Comment: In the text, "6 ips" is written. It would be better to explain "ips" before its usage.
Response: We replaced it as ‘6 intersection pairs’.

View more View less

Competing Interests

No competing interests were disclosed.

Back to all reports

Reviewer Report

31 Views

30 Jul 2020 | for Version 1

Zhaohui Steve Qin, Department of Biostatistics and Bioinformatics, Rollins School of Public Health, Emory University, Atlanta, GA, USA

31 Views Cite this report Responses(1)

Approved With Reservations

I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Figure 1C is not mentioned in the paper. Not sure why.

Is the rationale for developing the new software tool clearly explained?

Yes
Is the description of the software tool technically sound?

Yes
Are sufficient details of the code, methods and analysis (if applicable) provided to allow replication of the software development and its use by others?

Partly
Is sufficient information provided to allow interpretation of the expected output datasets and any results generated using the tool?

Yes
Are the conclusions about the tool and its performance adequately supported by the findings presented in the article?

Partly

Competing Interests

No competing interests were disclosed.

Reviewer Expertise

Bioinformatics.

Respond to this report

Responses (1)

Author Response

04 Jan 2021

John Feng, Deepstanding LLC, Crozet, 22932, USA

Response to Reviewer 1

Comment: Feng et al. described a novel method named seqpare, to measure the similarity between two sets of genomic intervals. I think the authors picked an important problem to work on and they presented a nice solution. The performance, from their studies, seem quite impressive. It is a nice new tool for solving such problems. but I do have a few issues with the paper.
Response: Thank you for your helpful comments and suggestions. We have revised the paper according to the specific comments, and we have also added a subset of the test data and instructions to the software page to ease the verification of the result.

Comment: I never get what exactly does “self-consistent” really mean. I do not think this is the same as the consistent used in statistics which is an asymptotic property. I think the authors should provide a better explanation of this term and why this is important for such a problem.
Response: The word "self-consistent" is used here with its literal meaning of "not having parts or aspects which are in conflict or contradiction with each other" (google dictionary). Being self-consistent is necessary for a definition, concept, metric or theory. We think it's a useful word and we have explained it in the Introduction. Nevertheless, we did remove it from the title since it may cause confusion without context.

Comment: Genomic intervals, in my opinion, should come with genomic coordinates, to indicate where does it come from in terms of the reference genome. Of course, this will not be the case if the data does not come from a model organism. I am surprised that such information is not used in their method. I think it is a disadvantage if this is not used. Since the problem can be much easier if order is being considered. I am interested to know what do the authors think about this.
Response: Genomic intervals in the standard BED file format contain essential genomic information such as Chromosome, start coordinate, end coordinate and strand, etc. Like all other tools mentioned in the paper, Seqpare uses BED file format. Seqpare does not require the intervals to be sorted, which is an advantage over tools that do require intervals to be sorted.

Comment: Figure 1C is not mentioned in the paper. Not sure why.
Response: Figure 1 shows four cases and Figure 1c is mentioned as case c in the last paragraph of the Methods section "Seqpare metric". We replaced ‘case c’ with ‘Figure 1c’.

View more View less

Competing Interests

No competing interests were disclosed.

Alongside their report, reviewers assign a status to the article:

Approved - the paper is scientifically sound in its current form and only minor, if any, improvements are suggested

Approved with reservations - A number of small changes, sometimes more significant revisions are required to address specific details and improve the papers academic merit.

Not approved - fundamental flaws in the paper seriously undermine the findings and conclusions

[1] Alekseyenko AV, Lee CJ: Nested containment list (NCList): A new algorithm for accelerating interval query of genome alignment and interval databases. Bioinformatics. 2007; 23(11): 1386–93. PubMed Abstract | Publisher Full Text

[2] Cormen TH, Leiserson CE, Rivest RL, et al.: Introduction to algorithms second edition. 2001. Reference Source

[3] Feng S, Feng J: deepstanding/seqpare: First release of Seqpare (Version v1.0.0). Zenodo. 2020. http://www.doi.org/10.5281/zenodo.3840051

[4] Feng J, Ratan A, Sheffield NC: Augmented interval list: A novel data structure for efficient genomic interval search. Bioinfomatics. 2019; 35(23): 4907–4911. Publisher Full Text

[5] Giardine B, Riemer C, Hardison RC, et al.: Galaxy: A platform for interactive large-scale genome analysis. Genome Res. 2005; 15(10): 1451–5. PubMed Abstract | Publisher Full Text | Free Full Text

[6] Jalili V, Matteucci M, Goecks J, et al.: Next generation indexing for genomic intervals. IEEE Transactions on Knowledge and Data Engineering. 2019; 31(10): 2008–2021. Publisher Full Text

[7] Kent WJ, Sugnet CW, Furey TS, et al.: The human genome browser at ucsc. Genome Res. 2002; 12(6): 996–1006. PubMed Abstract | Publisher Full Text | Free Full Text

[8] Layer RM, Pedersen BS, DiSera T, et al.: GIGGLE: A Search Engine for Large-Scale Integrated Genome Analysis. Nat Methods. 2018; 15(2): 123–126. PubMed Abstract | Publisher Full Text | Free Full Text

[9] Li H: Tabix: Fast Retrieval of Sequence Features From Generic TAB-delimited Files. Bioinformatics. 2011; 27(5): 718–9. PubMed Abstract | Publisher Full Text | Free Full Text

[10] Neph S, Kuehn MS, Reynolds AP, et al.: BEDOPS: high-performance genomic feature operations. Bioinformatics. 2012; 28(14): 1919–1920. PubMed Abstract | Publisher Full Text | Free Full Text

[11] Quinlan AR, Hall IM: BEDTools: A flexible suite of utilities for comparing genomic features. Bioinformatics. 2010; 26(6): 841–842. PubMed Abstract | Publisher Full Text | Free Full Text

[12] Richardson JE: Fjoin: Simple and efficient computation of feature overlaps. J Comput Biol. 2006; 13(8): 1457–1464. PubMed Abstract | Publisher Full Text

[13] Sheffield NC, Bock C: LOLA: Enrichment analysis for genomic region sets and regulatory elements in R and bioconductor. Bioinformatics. 2016; 32(4): 587–589. PubMed Abstract | Publisher Full Text | Free Full Text

Seqpare: a novel metric of similarity between genomic interval sets

Abstract

Keywords

Revised Amendments from Version 1

Introduction

Methods

Seqpare metric

Figure 1. Example cases for illustrating the Seqpare similarity metric.

Implementation

Operation

Results

A test with real genomic interval sets

Table 1. Comparison of Seqpare and GIGGLE similarity metrics: partial list of the search results from a collection of 100 interval sets, which contains the query set affyGnf1h.

Conclusion

Data availability

Source data

Underlying data

Software availability

References

Comments on this article Comments (0)

Open Peer Review

Comments on this article Comments (0)

Open Peer Review

Reviewer Status

Reviewer Reports

Comments on this article

Browse by related subjects

Competing Interests Policy

Stay Updated